2020春北师大版七下数学1.5平方差公式教学课件(共25张ppt)
文档属性
| 名称 | 2020春北师大版七下数学1.5平方差公式教学课件(共25张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 639.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-28 14:13:30 | ||
图片预览





文档简介
课件25张PPT。1.5 平方差公式单项式与单项式相乘,把它们的系数、相同字母的幂分别相乘,对于只在一个单项式中出现的字母,则连同它的指数一起作为积的一个因式.单项式乘以单项式法则: (1)系数相乘 (2)相同字母的幂相乘
(3)只在一个单项式中出
现的字母,则连同它的
指数一起作为积的一个
因式.
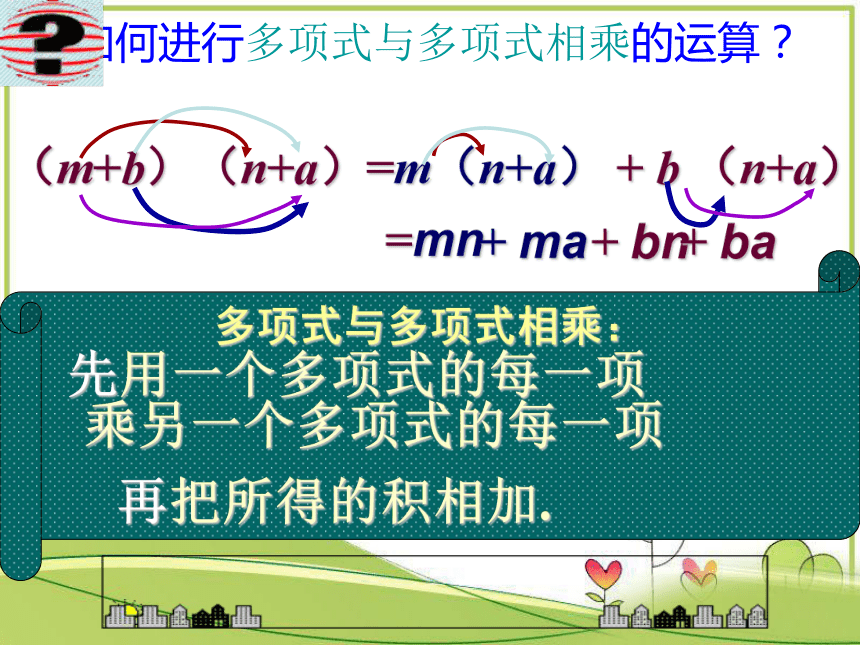
回顾与思考?② 再把所得的积相加.① 用单项式分别去乘多项式的每一项,单项式乘以多项式的 依据是 乘法对加法的分配律.① 不能漏乘:即单项式要乘遍多项式的每一项.② 去括号时注意符号的确定. 如何进行多项式与多项式相乘的运算? 先用一个多项式的每一项
乘另一个多项式的每一项再把所得的积相加.(m+b)(n+a)=m(n+a) + b (n+a)+ ma= x2 - 1=m2 - 4=4x2 - 1(1)两个相乘的多项式一个为两数和,另一个
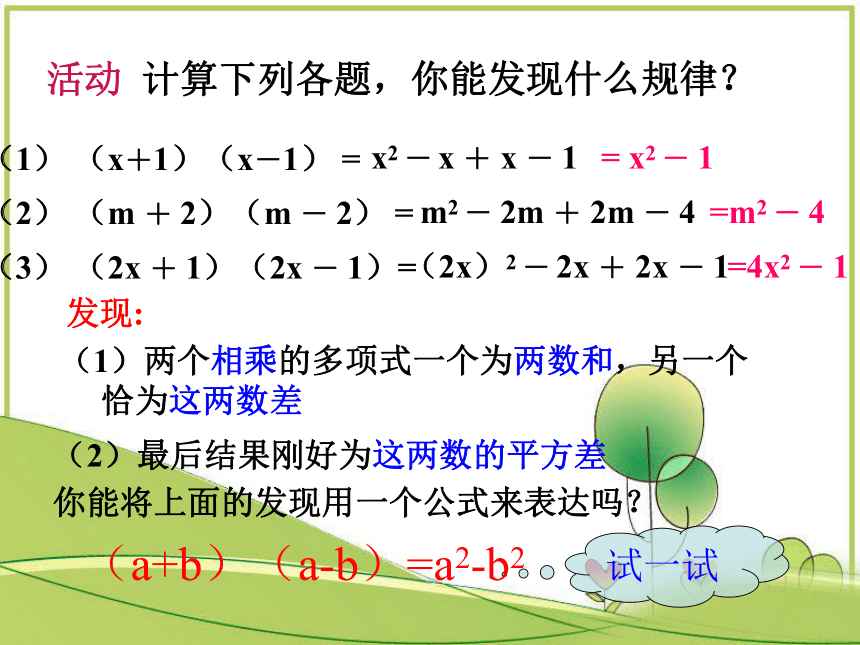
恰为这两数差(2)最后结果刚好为这两数的平方差你能将上面的发现用一个公式来表达吗?试一试
(a+b)(a-b)=a2-b2x2 - x + x - 1 m2 - 2m + 2m - 4(2x)2 - 2x + 2x - 1发现:活动 计算下列各题,你能发现什么规律? 请问你有几种方法求绿色部分面积?自主探究?
?
b长方形的面积=(a+b)(a-b)
剩下的面积=a2-b2
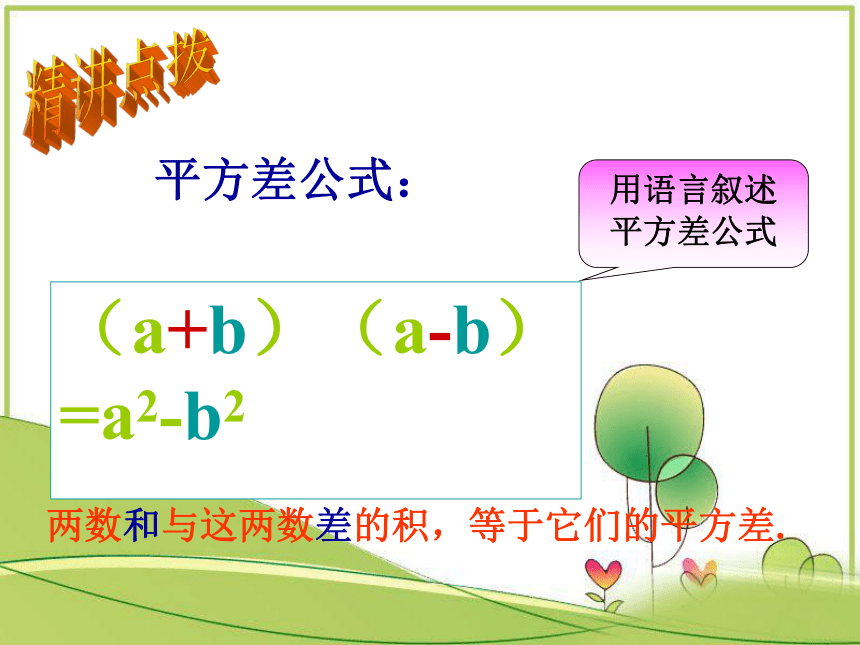
ab平方差公式:(a+b)(a-b)=a2-b2
两数和与这两数差的积,等于它们的平方差.用语言叙述平方差公式 精讲点拨
(a+b)(a-b)=(a)2-(b)2适当交换合理加括号平方差公式注:这里的两数可以是两个单项式也可以是两个多项式等等.(a +b)(a –b)=a2 - b2相同互为相反数1.左边两个多项式相乘,这两个二项式中有一项完全相同,另一项互为相反数.
2.右边是乘式中两项的平方差,即相同项的平方与相反项的平方差.
精讲点拨 口答下列各题:
(l)(a+b)(a+b)=_________
(2)(a-b)(b+a)=__________
(3)(-a-b)(-a+b)=________
(4)(a-b)(-a-b)=_________a2-b2a2-b2b2-a2b2-a2(1+x)(1-x)(-3+a)(-3-a)(0.3x-1)(1+0.3x)(1+a)(-1+a)找一找、填一填aba2-b21x-3a12-x2(-3)2-a2a1a2-12 0.3x1( 0.3x)2-12(a-b)(a+b)(1) (a+b)(?a?b);
(2) (a?b)(b?a) ;
(3) (a+2b)(2b+a);
(4) ?(a?b)(a+b);
(5) (?2x+y)(-y?2x). (不能) 下列式子可用平方差公式计算吗?为什么?如果能够,怎样计算? 第一个数不完全一样 (不能)两个数均互为相反数 (不能)两个数均相同(能) ?(a2 ?b2)= ?a2 + b2 (能) (?2x)2-y2=4x2-y2直接运用新知,解决第一层次问题自主探究:aba2-b2
y3y2-32a2-(3b)2a3b-mn(-m)2-n2a+bc(a+b)2-c2(a + b ) ( a – b ) = a2 - b2例1、用平方差公式计算
计算:(x+2y)(x-2y)解:原式= x2 - (2y)2=x2 - 4y21、先把要计算的式子与公式对照, 2、哪个是 a
哪个是 b例题例2 运用平方差公式计算:
(1) (3x+2 )( 3x-2 ) ;
(2) (b+2a)(2a-b);
(3) (-x+2y)(-x-2y).解:(1)(3x+2)(3x-2)=(3x)2-22=9x2-4;(2)(b+2a)(2a-b)=(2a+b)(2a-b)=(2a)2-b2=4a2-b2.(3) (-x+2y)(-x-2y)=(-x)2-(2y)2= x2-4y2试试就能行例3 计算:
(1) 102×98;
(2) (y+2) (y-2) – (y-1) (y+5) .解: (1) 102×98(y+2)(y-2)- (y-1)(y+5)= 1002-22=1000 – 4 =(100+2)(100-2)=9996= y2-22-(y2+4y-5)= y2-4-y2-4y+5= - 4y + 1.挑战自我知难而进1.计算 20042 - 2003×2005;拓展提升解:
20042 - 2003×2005= 20042 - (2004-1)(2004+1)= 20042- (20042-12 )= 20042- 20042+12 =12、利用平方差公式计算:(a-2)(a+2)(a2 + 4)
解:原式=(a2-4)(a2+4)
=a4-16
( )3.化简(x4+y4 )(x4+y4 )(x4+y4)知难而进灵活运用新知,解决第三层次问题 运用平方差公式计算:
(1)51×49
(2)(3x+4)(3x-4)-(2x+3)(3x-2)自主探究: a2 - b2 =(a+b)(a-b) 逆向思维训练:
(1) ( n - m )( )=n2-m2
( -2x +__ ) ( )=4x2-9y2
( -5 + a )( ) =25-a2
n+m-5 - a-2x-3y3y (2) 在式子(__-3a )(__+5b )的括号内横线上填入怎样的式子才能用平方差公式计算?
1.王红同学在计算(2+1)(22+1)(24+1)时,将积式乘以(2-1)得:
解:原式 = (2-1)(2+1)(22+1)(24+1)
=? (22-1)(22+1)(24+1)
=? (24-1)(24+1)
=? 28-1
你能根据上题计算: (2+1)(22+1)(24+1)(28+1) (216+1) 的结果吗?课后延伸1. 试用语言表述平方差公式 (a+b)(a?b)=a2?b2.两数和与这两数差的积,等于它们的平方差.2.应用平方差公式时要注意一些什么?运用平方差公式时,要紧扣公式的特征,找出相等
的“项”和符号相反的“项”,然后应用公式; 变成公式标准形式后,再用公式. 或提取一个公因数,要利用加法交换律,3. 对于不符合平方差公式标准形式者,小结
(3)只在一个单项式中出
现的字母,则连同它的
指数一起作为积的一个
因式.
回顾与思考?② 再把所得的积相加.① 用单项式分别去乘多项式的每一项,单项式乘以多项式的 依据是 乘法对加法的分配律.① 不能漏乘:即单项式要乘遍多项式的每一项.② 去括号时注意符号的确定. 如何进行多项式与多项式相乘的运算? 先用一个多项式的每一项
乘另一个多项式的每一项再把所得的积相加.(m+b)(n+a)=m(n+a) + b (n+a)+ ma= x2 - 1=m2 - 4=4x2 - 1(1)两个相乘的多项式一个为两数和,另一个
恰为这两数差(2)最后结果刚好为这两数的平方差你能将上面的发现用一个公式来表达吗?试一试
(a+b)(a-b)=a2-b2x2 - x + x - 1 m2 - 2m + 2m - 4(2x)2 - 2x + 2x - 1发现:活动 计算下列各题,你能发现什么规律? 请问你有几种方法求绿色部分面积?自主探究?
?
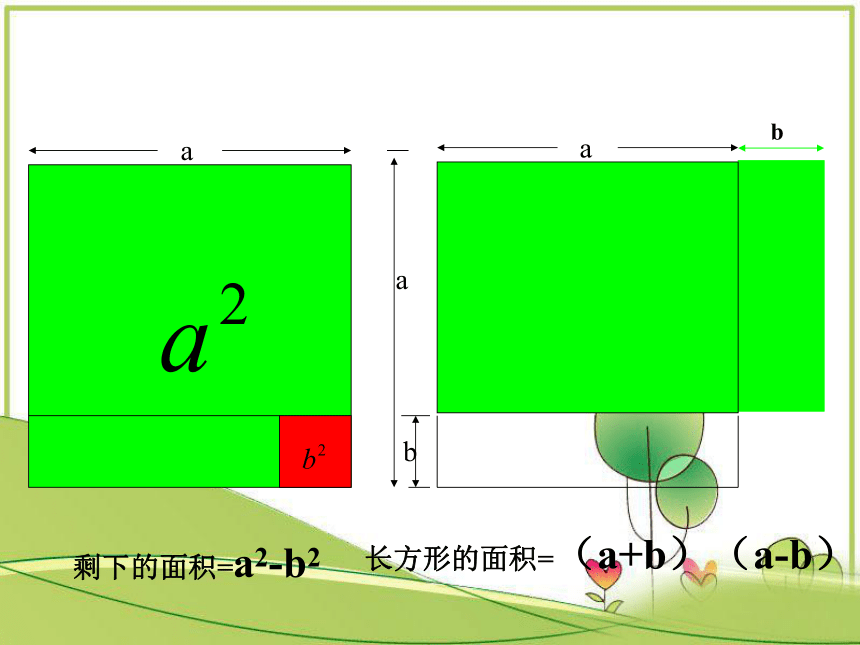
b长方形的面积=(a+b)(a-b)
剩下的面积=a2-b2
ab平方差公式:(a+b)(a-b)=a2-b2
两数和与这两数差的积,等于它们的平方差.用语言叙述平方差公式 精讲点拨
(a+b)(a-b)=(a)2-(b)2适当交换合理加括号平方差公式注:这里的两数可以是两个单项式也可以是两个多项式等等.(a +b)(a –b)=a2 - b2相同互为相反数1.左边两个多项式相乘,这两个二项式中有一项完全相同,另一项互为相反数.
2.右边是乘式中两项的平方差,即相同项的平方与相反项的平方差.
精讲点拨 口答下列各题:
(l)(a+b)(a+b)=_________
(2)(a-b)(b+a)=__________
(3)(-a-b)(-a+b)=________
(4)(a-b)(-a-b)=_________a2-b2a2-b2b2-a2b2-a2(1+x)(1-x)(-3+a)(-3-a)(0.3x-1)(1+0.3x)(1+a)(-1+a)找一找、填一填aba2-b21x-3a12-x2(-3)2-a2a1a2-12 0.3x1( 0.3x)2-12(a-b)(a+b)(1) (a+b)(?a?b);
(2) (a?b)(b?a) ;
(3) (a+2b)(2b+a);
(4) ?(a?b)(a+b);
(5) (?2x+y)(-y?2x). (不能) 下列式子可用平方差公式计算吗?为什么?如果能够,怎样计算? 第一个数不完全一样 (不能)两个数均互为相反数 (不能)两个数均相同(能) ?(a2 ?b2)= ?a2 + b2 (能) (?2x)2-y2=4x2-y2直接运用新知,解决第一层次问题自主探究:aba2-b2
y3y2-32a2-(3b)2a3b-mn(-m)2-n2a+bc(a+b)2-c2(a + b ) ( a – b ) = a2 - b2例1、用平方差公式计算
计算:(x+2y)(x-2y)解:原式= x2 - (2y)2=x2 - 4y21、先把要计算的式子与公式对照, 2、哪个是 a
哪个是 b例题例2 运用平方差公式计算:
(1) (3x+2 )( 3x-2 ) ;
(2) (b+2a)(2a-b);
(3) (-x+2y)(-x-2y).解:(1)(3x+2)(3x-2)=(3x)2-22=9x2-4;(2)(b+2a)(2a-b)=(2a+b)(2a-b)=(2a)2-b2=4a2-b2.(3) (-x+2y)(-x-2y)=(-x)2-(2y)2= x2-4y2试试就能行例3 计算:
(1) 102×98;
(2) (y+2) (y-2) – (y-1) (y+5) .解: (1) 102×98(y+2)(y-2)- (y-1)(y+5)= 1002-22=1000 – 4 =(100+2)(100-2)=9996= y2-22-(y2+4y-5)= y2-4-y2-4y+5= - 4y + 1.挑战自我知难而进1.计算 20042 - 2003×2005;拓展提升解:
20042 - 2003×2005= 20042 - (2004-1)(2004+1)= 20042- (20042-12 )= 20042- 20042+12 =12、利用平方差公式计算:(a-2)(a+2)(a2 + 4)
解:原式=(a2-4)(a2+4)
=a4-16
( )3.化简(x4+y4 )(x4+y4 )(x4+y4)知难而进灵活运用新知,解决第三层次问题 运用平方差公式计算:
(1)51×49
(2)(3x+4)(3x-4)-(2x+3)(3x-2)自主探究: a2 - b2 =(a+b)(a-b) 逆向思维训练:
(1) ( n - m )( )=n2-m2
( -2x +__ ) ( )=4x2-9y2
( -5 + a )( ) =25-a2
n+m-5 - a-2x-3y3y (2) 在式子(__-3a )(__+5b )的括号内横线上填入怎样的式子才能用平方差公式计算?
1.王红同学在计算(2+1)(22+1)(24+1)时,将积式乘以(2-1)得:
解:原式 = (2-1)(2+1)(22+1)(24+1)
=? (22-1)(22+1)(24+1)
=? (24-1)(24+1)
=? 28-1
你能根据上题计算: (2+1)(22+1)(24+1)(28+1) (216+1) 的结果吗?课后延伸1. 试用语言表述平方差公式 (a+b)(a?b)=a2?b2.两数和与这两数差的积,等于它们的平方差.2.应用平方差公式时要注意一些什么?运用平方差公式时,要紧扣公式的特征,找出相等
的“项”和符号相反的“项”,然后应用公式; 变成公式标准形式后,再用公式. 或提取一个公因数,要利用加法交换律,3. 对于不符合平方差公式标准形式者,小结
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
