湘教版 八下数学1.2直角三角形的性质和判定2课时练含答案(PDF版)
文档属性
| 名称 | 湘教版 八下数学1.2直角三角形的性质和判定2课时练含答案(PDF版) |  | |
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-28 23:04:15 | ||
图片预览




文档简介
!!"
!
直角三角形的性质和判定!
"
"! "
!前置诊断"检测你的基础#助力新课学习
!
!!
若%
,0)
&
&
',
&
02,0-
!则
-
的值为 %
!!
&
*!2 ,!9$- .!62 /!$-
"!
已知一个正方形的面积为
$&
!则它的边长为 %
!!
&
*!- ,!&槡+ .!+槡& /!)
#!
已知直角三角形的两条直角边长分别为
+
和
)
!则这个三角形的面积为 %
!!
&
*!- ,!+! .!$& /!3
!前置巩固"如果你没有全部正确#务必回顾复习
!
$!
完全平方公式"%
*9-
&
&
'*
&
9&*-0-
&
!
&!
正数有一个正的平方根!这个平方根叫做算术平方根
!
+!
直角三角形的面积等于两条直角边的积的一半
!
!!
直角三角形中#三边之间有特殊的数量关系吗$ 今天我们来探究直角三角形三边之
间的数量关系
!
!!
勾股定理"直角三角形两直角边
*
#
-
的平方和#等于斜边
.
的平方
%
$
&这一定理只对直角三角形适用!对锐角三角形和钝角三角形不适用
!
利用公式
时!要分清是直角边还是斜边
!
%
&
&直角三角形中!已知任意两边!可以求出第三边
!*
&
0-
&
'.
&
!可化为"
*
&
'.
&
6-
&
!
-
&
'.
&
6*
&
%
*
!
-
为直角边!
.
为斜边&
!
%
+
&这一定理把角度关系转化为数量关系!是转化思想的一个典范
!
"!
勾股定理可以用图形的面积证明
体现了数形结合的数学思想!把直角三角形这个(形*与三边关系这一(数*结合起
来
!
教科书中给出了勾股定理的一种证明方法!历史上有许多人对勾股定理进行了研究!
给出了勾股定理的一些证明方法!感兴趣的同学可以自行查阅有关资料
!
#!
勾股定理又称商高定理!毕达哥拉斯定理!百牛定理
例
!
!
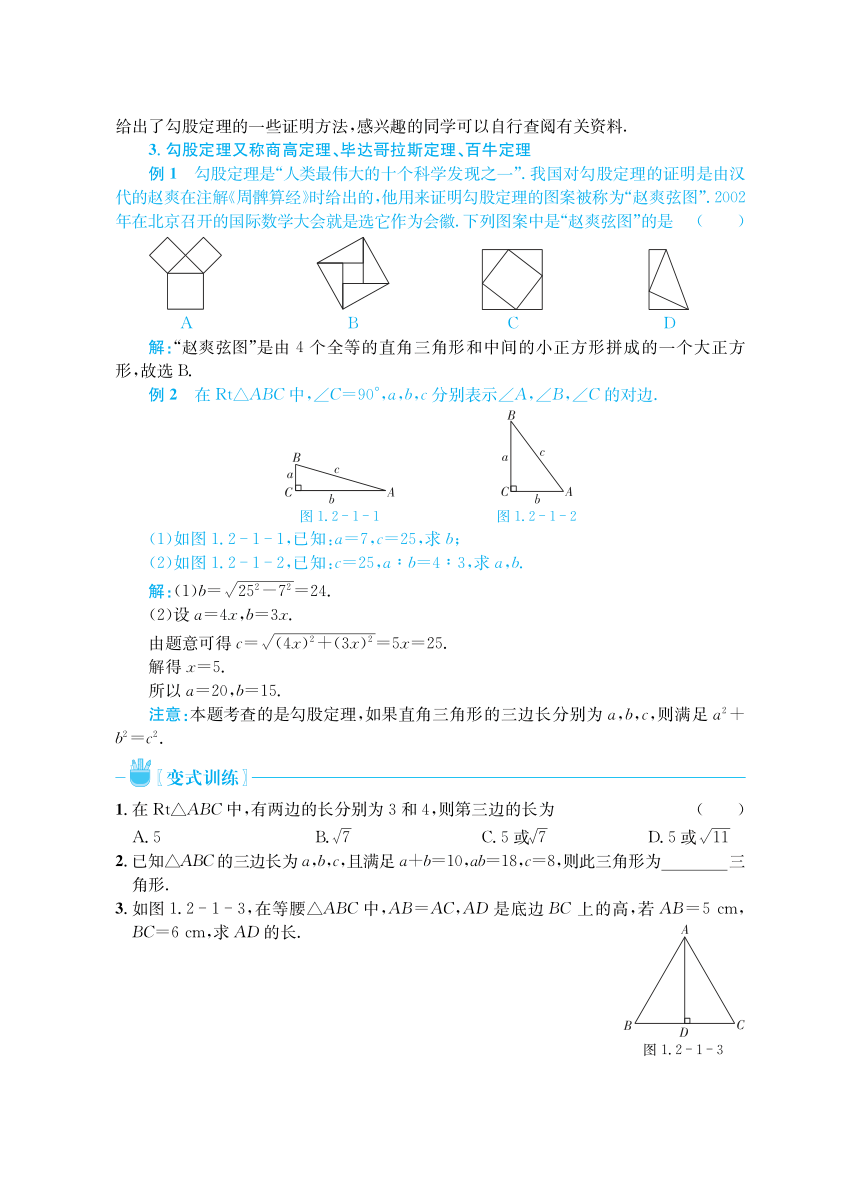
勾股定理是(人类最伟大的十个科学发现之一*
!
我国对勾股定理的证明是由汉
代的赵爽在注解,周髀算经-时给出的!他用来证明勾股定理的图案被称为(赵爽弦图*
!&""&
年在北京召开的国际数学大会就是选它作为会徽
!
下列图案中是(赵爽弦图*的是 %
!!
&
* , . /
解"(赵爽弦图*是由
)
个全等的直角三角形和中间的小正方形拼成的一个大正方
形!故选
,!
例
"
!
在
45
"
#$%
中!
#
%'1"(
!
*
!
-
!
.
分别表示
#
#
!
#
$
!
#
%
的对边
!
图
$!& $ $
!!!!!!图
$!& $ &
%
$
&如图
$!& $ $
!已知"
*'3
!
.'&!
!求
-
'
%
&
&如图
$!& $ &
!已知"
.'&!
!
*%-')%+
!求
*
!
-!
解"%
$
&
-' &!
&
63槡 &'&)!
%
&
&设
*'),
!
-'+,!
由题意可得
.'
%
),
&
&
0
%
+,
&槡 &'!,'&!!
解得
,'!!
所以
*'&"
!
-'$!!
注意"本题考查的是勾股定理!如果直角三角形的三边长分别为
*
!
-
!
.
!则满足
*
&
0
-
&
'.
&
!
!!
在
45
"
#$%
中!有两边的长分别为
+
和
)
!则第三边的长为 %
!!
&
*! ,!槡3 .!或槡3 /!或槡$$
"!
已知
"
#$%
的三边长为
*
!
-
!
.
!且满足
*0-'$"
!
*-'$2
!
.'2
!则此三角形为
!!!!
三
角形
!
#!
如图
$!& $ +
!在等腰
"
#$%
中!
#$'#%
!
#&
是底边
$%
上的高!若
#$'!8#
!
!
图
$!& $ +
$%'-8#
!求
#&
的长
!
$!
勾股定理是刻画直角三角形三边关系的重要定理!一定要熟记
!
在直角三角形中!
已知任意两边!可以求出第三边
!
&!
利用勾股定理解题时!要分清直角边和斜边!题目没有指明斜边时!要分类讨论
!
!!
在
45
"
#$%
中!
#
%'1"(
!若
#$'$+
!
$%'!
!则
#%
的长为 %
!!
&
*! ,!2 .!$& /!$2
"!
在
45
"
#$%
中!有两边的长分别
!
和
$&
!则第三边长为
!!!!
!
#!
直角三角形的斜边长为
!8#
!两直角边长之比为
+%)
!那么这个直角三角形的周长为
!!!!
!
$!
如图
$!& $ )
!在
45
"
#$%
中!
#
#%$'1"(
!以它的各边为边向外作三个正方形!面
积分别为
"
$
!
"
&
!
"
+
!已知
"
$
'-
!
"
&
'2
!则
"
+
'
!!!!
!
图
$!& $ )
%!
如图
$!& $ !
!在
45
"
#$%
中!
#
%'1"(
!
$%'-
!
#%'2
!
#$
的垂直平分线
&'
交
#$
于点
&
!交
#%
于点
'
!连接
$'!
%
$
&求
#&
的长'
%
&
&求
#'
的长
!
!
图
$!& $ !
!!"
!
直角三角形的性质和判定!
"
"!
"
"
!前置诊断"检测你的基础#助力新课学习
!
!!
在
45
"
#$%
中!
#
%'1"(
!
#$'$"8#
!
#%'28#
!则
$%
长为 %
!!
&
*!-8# ,!$)8# .!$&8# /!$28#
"!
在
45
"
#$%
中!
#
$'1"(
!
#$'!
!
$%'$&
!则
#%
的长为 %
!!
&
*!3 ,!槡$$1 .!$+ /!$2
#!
在
45
"
#$%
中!有两边的长分别为
+
和
!
!则第三边的长为 %
!!
&
*!) ,!槡&1 .!)或槡&1 /!)或槡+)
!前置巩固"如果你没有全部正确#务必回顾复习
!
$!
勾股定理"直角三角形的两条直角边的平方和!等于斜边的平方
!
&!
全等三角形的性质"全等三角形的对应边相等!对应角相等
!
!!
我们已经学习了勾股定理#运用勾股定理可以解决一些几何问题和实际问题
!
!!
利用勾股定理解决实际问题!要善于从实际问题中抽象出几何模型!再画出几何
图形!从而把实际问题转化为数学问题
!
"!
构造直角三角形模型后!确定斜边$直角边'不是直角三角形的要通过作垂线%或
平行线&构造出直角三角形
!
#!
在实际问题中!常常默认电线杆$旗杆$大树$建筑物等垂直于地面
!
$!
求解方位角的问题时!东西方向和南北方向在平面中恰好垂直!因而常利用这一
垂直关系来建立直角三角形
!
%!
要注意用转化$数形结合$方程等思想来解决相关问题
!
例
!
!
数学综合实验课上!同学们在测量学校旗杆的高度时发现"将旗杆顶端升旗用的
绳子垂到地面还多
&#
'当把绳子的下端拉开
2#
后!下端刚好接触地面!如图
$!& & $!
根据以上数据!同学们准确求出了旗杆的高度!你知道他们是如何计算出来的吗#
图
$!& & $
解"设旗杆高
,#
!则绳子长为%
,0&
&
#!
:
旗杆垂直于地面!
;
旗杆$绳子与地面构成直角三角形
!
由题意列式为
,
&
02
&
'
%
,0&
&
&
!解得
,'$!!
;
旗杆的高度为
$!#!
注意"由题可知!旗杆$绳子与地面构成直角三角形!根据题中数据!用勾股定理即可
求解
!
本题考查的是勾股定理的应用!根据题意找出直角三角形是解答此题的关键
!
!
图
$!& & &
例
"
!
如图
$!& & &
!甲乙两船从港口
#
同时出发!甲船以
$-
海里+
7
的速度向北偏东
)"(
方向航行!乙船向南偏东
!"(
方向航
行!
+7
后!甲船到达
%
岛!乙船到达
$
岛
!
若
%
!
$
两岛相距
$"&
海里!
问乙船的航速是多少#
解"
:
#
$#%'$2"(6)"(6!"('1"(
!
;
"
#$%
是直角三角形!
;#%
&
0#$
&
'$%
&
!
:#%'$-<+')2
%海里&!
$%'$"&
海里!
;#$' $%
&
6#%槡 &' $"&&6)2槡 &'1"%海里&!
:
乙船航行时间为
+7
!
;
乙船的航速为
1"=+'+"
%海里+
7
&
!
答"乙船的航速是
+"
海里+
7!
注意"先根据方位角的定义证得
"
#$%
是直角三角形!再求出
#%
的长度!根据勾股
定理求得
#$
的长!然后根据乙船的航行时间即可解题
!
本题考查了方位角问题及勾股
定理的应用!理解方位角的定义证得
"
#$%
是直角三角形是解答本题的关键
!
图
$!& & +
!
!!
一云梯
#$
长
&!#
!如图
$!& & +
所示斜靠在一面墙上!云梯
底端离墙
3#
!如果云梯的顶端下滑了
)#
!那么它的底端在水
平方向滑动
$$/
的长是 %
!!
&
*!$"#
,!2#
.!-#
/!)#
!
图
$!& & )
"!
老师要求同学们设计一个测量某池塘两端
#
!
$
距离的方案!王兵设
计的方案如下"如图
$!& & )
!在池塘外选一点
%
!测得
#
%#$'1"(
!
#
%'+"(
!
#%'+-#
!则可知
#$
的距离为 %
!!
&
*! 槡$1 +# ,!$1#
.! 槡$& +# /! 槡$& &#
#!
如图
$!& & !
是一株美丽的勾股树!其中所有的四边形都是正方形!所有的三角形都
是直角三角形
!
若正方形
#
!
$
!
%
!
&
的边长分别是
+
!!
&
!
+
!则最大正方形
'
的面积是
%
!!
&
图
$!& & !
*!$+ ,!&- .!+) /!)3
$!
如图
$!& & -
!甲轮船以
&)
海里+
7
的速度离开港口
+
向东南方向航行!乙轮船在同
时同地向西南方向航行!已知它们离开港口
+
半小时后分别到达
$
!
#
两点!且相距
$!
海里!问乙轮船每小时航行多少海里#
!
图
$!& & -
$!
利用勾股定理解决实际问题!要抽象出几何图形!找到直角三角形!同时注意问题
中变与不变的线段长度
!
&!
还可利用勾股定理求由几个正方形或圆构成的图形的面积
!
!
图
$!& & 3
!!
如图
$!& & 3
!一棵大树在离地面
-#
高的
$
处断裂!树顶
#
落在离树底部
%
的
2#
处!则大树断裂之前的高度为 %
!!
&
*!$-# ,!$!#
.!&)# /!&$#
"!
如图
$!& & 2
!公路
#%
!
$%
互相垂直!公路
#$
的中点
0
与点
%
被湖隔开!若测得
#%'$&>#
!
$%'$->#
!则
0
!
%
两点之间的距离为 %
!!
&
*!$+># ,!$&># .!$$># /!$">#
图
$!& & 2
!!!!!!! 图
$!& & 1
#!
如图
$!& & 1
!在
45
"
#$%
中!
#
#%$'1"(
!则三个半圆的面积关系是 %
!!
&
*!"
$
0"
&
&
"
+
,!"
$
0"
&
'"
+
.!"
$
0"
&
'
"
+
/!"
&
$
0"
&
&
'"
&
+
$!
如图
$!& & $"
!一艘船由
#
港沿北偏东
-"(
方向航行
$">#
至
$
港!然后再沿北偏
西
+"(
方向航行
$">#
至
%
港
!
%
$
&求
#
!
%
两港之间的距离%结果精确到
"!$>#
!参考数据"槡&
%
$!)$)
!槡+
%
$!3+&
&'
%
&
&确定
%
港在
#
港的什么方向
!
!
图
$!& & $"
%!
甲同学在拼图探索活动中发现!用
)
个形状大小完全相同的直角三角形%直角边长分
别为
*
!
-
!斜边长为
.
&!可以拼成如图
$!& & $$
所示的正方形!并由此得出了关于
*
&
!
-
&
!
.
&的一个等式
!
图
$!& & $$
!!!! 图
$!& & $&
%
$
&请你写出这一结论"
!!!!
!并给出验证过程'
%
&
&试用上述结论解决问题"如图
$!& & $&
!
)
是
45
"
#$%
斜边
#$
上的一个动点!
已知
#%'!
!
#$'$+
!求
)%
的最小值
!
!
!!"
!
直角三角形的性质和判定!
"
"!
#
"
!前置诊断"检测你的基础#助力新课学习
!
!!
若等腰三角形的腰长为
$+
!底边长为
$"
!则底边上的高为 %
!!
&
*!- ,!3 .!1 /!$&
"!
下列命题的逆命题是假命题的是 %
!!
&
*!
直角三角形中的两个锐角互余
,!
直角三角形斜边上的中线等于斜边的一半
.!
两个全等三角形的对应角相等
/!
两个全等三角形的对应边相等
#!
请写出(直角三角形的两条直角边
*
$
-
和斜边
.
满足关系式"
*
&
0-
&
'.
&
*的逆命题"
!!!!!!!!!!!!!!!! !
!
!前置巩固"如果你没有全部正确#务必回顾复习
!
$!
勾股定理"直角三角形的两条直角边
*
!
-
的平方和!等于斜边
.
的平方
!
&!
互逆命题"对于两个命题!如果一个命题的条件和结论分别是另一个命题的结论和
条件!我们把这样的两个命题称为互逆命题!其中一个叫作原命题!另一个叫作逆命题
!
!!
我们知道%直角三角形两直角边的平方和#等于斜边的平方&#那么反过来#已知一个
三角形有两边的平方和等于第三边的平方#能判定这个三角形是直角三角形吗$
!!
勾股定理的逆定理"如果三角形的三条边长
*
!
-
!
.
满足关系式"
*
&
0-
&
'.
&
!那么
这个三角形是直角三角形
!
勾股定理的逆定理是判定一个三角形为直角三角形的方法!不能叙述为(斜边的平
方等于两条直角边的平方和*
!
在判定一个三角形为直角三角形之前!不能说哪条边为斜
边!哪条边为直角边
!
这一定理把线段长度关系转化为角度关系!是由(数*到(形*!体现了数形结合的转
化思想
!
"!
勾股数"满足
*
&
0-
&
'.
&的三个正整数称为勾股数
!
勾股数是一组正整数
!
以一组勾股数的长度为三边的三角形!是一个直角三角形
!
常见的勾股数有"
+
!
)
!'
!
!
$&
!
$+
'
3
!
&)
!
&!
'
2
!
$!
!
$3
'
1
!
)"
!
)$
等
!
对于任何一组勾股
数!将各数乘相同整教!则能得到另一组勾股数
!
如"由
+
!
)
!是一组勾股数!可得到
$2
!
&)
!
+"
也是勾股数
!
!
图
$!& + $
例
!
!
如图
$!& + $
!正方形网格中每个小方格的边长为
$
!且点
#
!
$
!
%
均为格点!通过计算判断
"
#$%
的形状
!
解"由勾股定理得
#%
&
')
&
0&
&
'&"
!
$%
&
'&
&
0$
&
'!
!
#$
&
'
+
&
0)
&
'&!
!
;#%
&
0$%
&
'#$
&
!
;
"
#$%
是直角三角形
!
例
"
!
如图
$!& + &
!在
"
#$%
中!
$&
$
#%
!
#$'&"
!
$%'$!
!
%&'1!
!
图
$!& + &
%
$
&求
#%
的长'
%
&
&判断
"
#$%
的形状并证明
!
解"%
$
&在
"
#$%
中!
:$&
$
#%
!
#$'&"
!
$%'$!
!
&%'1
!
;$&' $!
&
61槡 &'$&!
;#&' &"
&
6$&槡 &'$-!
;#%'#&0&%'$-01'&!!
%
&
&
:#%'&!
!
$%'$!
!
#$'&"
!
&"
&
0$!
&
'&!
&
!
;
"
#$%
是直角三角形
!
!!
下列四组线段!可以构成直角三角形的是 %
!!
&
*!)
!!
- ,!
!
$&
!
$+ .!&
!
+
!
) /!$
!槡&!+
"!
适合下列条件的
"
#$%
中!直角三角形的个数为 %
!!
&
%
$
&
*'-
!
#
#')!(
' %
&
&
#
#'+&(
!
#
$'!2(
'
%
+
&
*'-
!
-'2
!
.'$"
' %
)
&
*'-
&
!
-'2
&
!
.'$"
&
!
*!$ ,!& .!+ /!)
#!
已知
*
!
-
!
.
是
"
#$%
的三边长!且满足关系式
.
&
6*
&
6-槡 &0 *6- '"!则
"
#$%
的
形状为
!!!!!!
!
$!
如图
$!& + +
!在
"
#$%
中!已知
#$'#%'$+8#
!
&
是
#$
上一点!且
%&'
$&8#
!
$&'28#!
!
图
$!& + +
%
$
&求证"
"
#&%
是直角三角形'
%
&
&求
$%
的长
!
$!
用勾股定理的逆定理判定直角三角形的步骤"
%
$
&先找出最长的一条边
.
!算出
.
&
!
%
&
&计算两条较短边
*
!
-
的平方和
!
%
+
&如有
*
&
0-
&
'.
&
!则可判定这个三角形是直角三角形'否则不能判定
!
如果不能确
定最长的边!则需分类讨论
!
&!
应用勾股定理及其逆定理时应分清条件和结论
!
!!
在
"
#$%
中!
#$'$&8#
!
#%'18#
!
$%'$!8#
!则
"
#$%
的面积
"
"
#$%
是%
!!
&
*!$"28#
&
,!)8#
&
.!$2"8#
&
/!1"8#
&
"!
已知
*槡6$&0 -% &6! & 0 .6$+ '"!则以*!-!.为三边的三角形的形状是
!!!!!!!!
!
#!
如图
$!& + )
!在
)<+
的正方形网格中!每个小正方形的边长都为
$!
%
$
&线段
#$
的长为
!!!!
'
%
&
&在图中作出线段
'(
!使得
'(
的长为槡$+!判断#$!%&!'(三条线段能否构成直
角三角形!并说明理由
!
!
图
$!& + )
$!
如图
$!& + !
所示有一块铁皮%图中阴影部分&!测得
#$'+
!
$%')
!
%&'$&
!
#&'
$+
!
#
$'1"(!
求阴影部分的面积
!
!
图
$!& + !
%!
如图
$!& + -
!在四边形
#$%&
中!
#$'$%'%&'#&')
!
#
&#$'
#
$'
#
%'
#
&'1"(
!
'
!
(
分别是
$%
和
%&
边上的点!且
%''
$
)
$%
!
(
为
%&
的中点!问
"
#'(
!
图
$!& + -
是什么三角形# 并说明理由
!
!!"
"#$#%&'()
*+
!
"
"!"
!前置诊断"
!!!
!
"!"
!
#!&
!变式训练"
!!*
"!
直角
!
!
(8)
"
(
-'+
(
4(5'$-3,
#
.*
(
-3,
#
1(
(
8)
(
-*
(
!
1
#
"$%
是直角三角形
!
#!,67
!效果检测"
!!*
!
"!'#
或槡''2!#!'(67!
$!',
!
.
"
"%$-2+%
#
+
'
-3
#
+
(
-$
#
1"%
(
-3
#
$%
(
-$
#
1"$
(
-"%
(
8$%
(
-',!
1+
#
-',!
%!
!
'
"在
/0
#
"$%
中#
.
"
%-2+%
#
$%-3
#
"%-$
#
1"$- 3
(
8$槡 (-'+!
.#,
垂直平分
"$
#
1"#-$#-)!
!
(
"
.#,
垂直平分
"$
#
1$,-",!
设
,%--
#则
",-$,-$4-!
故
3
(
8-
(
-
!
$4-
"
(
!
解得
--
9
,
!
1",-$4
9
,
-
()
,
!
!!"
"#$#%&'()
*+
!
"
"!
"
"
!前置诊断"
!!&
!
"!*
!
#!!
!
!变式训练"
!!"
!
由题意可得$
"$-()7
#
'$-97
#
则
'"- "$
(
4'$槡 (- ()(49槡 (-(,!7"!
当云梯的顶端下滑了
,7
#则
".'-(,4,-
(+
!
7
"
!
故
'$.- ()
(
4(+槡 (-')!7"#
则
$$.-'$.4'$-$7!
故选
"!
"!*
!
.
"
%"$-2+%
#
"
%-#+%
#
"%-#37
#
设
"$--7
#则
$%-(-7!
1"%
(
8"$
(
-$%
(
#
即
#3
(
8-
(
-
!
(-
"
(
!
解得
--'(槡#!故选*!
#!!
!
由勾股定理得#正方形
/
的面积
-
正方形
"
的面积
8
正方形
$
的面积
-#
(
8)
(
-#,!
同理#正方形
0
的面积
-
正方形
%
的面积
8
正
方形
#
的面积
-(
(
8#
(
-'#!
1
正方形
,
的面积
-
正方形
/
的面积
8
正方
形
0
的面积
-,9!
故选
!!
$!.
甲轮船向东南方向航行#乙轮船向西南方向
航行#
1"'
$
$'!
.
甲轮船以
(,
海里%
:
的速度航行了半小时#
1'$-(,5+!)-'(
!海里"
!
又
."$-')
海里#
1
在
/0
#
"'$
中#
"' - "$
(
4'$槡 ( -
')
(
4'(槡 (-2!海里"#
1
乙轮船每小时航行
2;+!)-'$
!海里"
!
!效果检测"
!!&
!
"!!
#!"
!
.
"
"%$-2+%
#
1"%
(
8$%
(
-"$
(
!
.+
'
-
'
(
!
"%
! "
(
(
-
!
&
"%
(
$
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
#
+
(
-
'
(
!
$%
! "
(
(
-
!
&
$%
(
$
#
+
#
-
'
(
!
"$
! "
(
(
-
!
&
"$
(
$
#
1+
'
8+
(
-
!
$
!
"%
(
8$%
(
"
-
!
$
"$
(
-+
#
!
即
+
'
8+
(
-+
#
!
故选
"!
$!
!
'
"由题意可得
"
&$%-#+%
#
"
1"$-3+%!
1
"
%$2-3+%
#
"
$"3-#+%
#
1
"
"$2-#+%
#
1
"
"$%-2+%!
."$-$%-'+<7
#
1"%- "$
(
8$%槡 ( 槡-'+ ('',!'!<7"!
故
"
#
%
两港之间的距离约为
',!'<7!
!
(
"由!
'
"知#
#
"$%
为等腰直角三角形#
1
"
$"%-,)%
#
1
"
%"1-3+%4,)%-')%!
1%
港在
"
港的北偏东
')%
方向上
!
%!
!
'
"结论$
(
(
8)
(
-*
(
!
证明$
.
阴影部分的面积
-,5
'
(
()-(()
#
阴影部分的面积
-
!
(8)
"
(
4*
(
#
1
!
(8)
"
(
4*
(
-(()
#即
(
(
8)
(
-*
(
!
!
(
"在
/0
#
"$%
中#
"%-)
#
"$-'#
#
1)
(
8$%
(
-'#
(
#
解得
$%-'(!
当
%&
$
"$
时#
&%
最短#
此时'
(
$%5"%-
'
(
"$5&%
#
即
&%-
)5'(
'#
-
3+
'#
#
1&%
的最小值为3+
'#
!
!!"
"#$#%&'()
*+
!
"
"!
#
"
!前置诊断"
!!!
!
"!*
!
如果一个命题的条件和结论分别是另一个
命题的结论和条件#那么这两个命题叫作互逆
命题
!
选项
*
的逆命题是$对应角相等的两个三
角形是全等三角形#显然是假命题
=
故选
*=
#!
如果三角形的三条边长
(
#
)
#
*
满足关系式$
(
(
8)
(
-*
(
#那么这个三角形是直角三角形
!变式训练"
!!"
"!*
!
直角三角形是!
'
"!
(
"!
#
"#故选
*!
#!
等腰直角三角形
$!
!
'
"
."$-'#67
#
$#-$67
#
1"#-"$4$#-)67!
."%-'#67
#
%#-'(67
#
1"#
(
8%#
(
-"%
(
#
1
"
"#%-2+%
#
故
#
"#%
是直角三角形
!
!
(
"在
/0
#
$#%
中#
"
$#%-'$+%42+%-2+%
#
$#-$67
#
%#-'(67
#
由勾股定理得
$%- $#
(
8%#槡 (- $(8'(槡 (-
,槡'#!67"!
!效果检测"
!!"
!
"!
直角三角形
#!
!
'
"槡)
!
(
"如图#
,/- #
(
8(槡 (-槡'##%#- ((8(槡 (-
(槡(!
.%#
(
8"$
(
-$8)-'#
#
,/
(
-'#
#
1%#
(
8"$
(
-,/
(
#
1"$
#
%#
#
,/
三条线段可以构成直角三角形
!
$!
连接
"%!
在
#
"$%
中#
.
"
$-2+%
#
"$-#
#
$%-,
#
1"%- #
(
8,槡 (-)!
.%#-'(
#
"#-'#
#
"%-)
#
1"%
(
8%#
(
-"#
(
#
1
#
"%#
是直角三角形
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
#
1+
阴影
-+
#
"%#
4+
#
"$%
-
'
(
5)5'(4
'
(
5
#5,-#+43-(,!
%!
直角三角形
!
理由如下$
."$-$%-%#-"#-,
#
%,-
'
,
$%
#
1,%-'
#
$,-#!
./
为
%#
的中点#
1#/-/%-(!
.
"
#"$-
"
$-
"
%-
"
#-2+%
#
1,/- (
(
8'槡 ( 槡- )#
"/- ,
(
8(槡 ( 槡- (+#
",- ,
(
8#槡 (-)#
1",
(
-,/
(
8"/
(
!
1
#
",/
是直角三角形
!
! ! ! !
!
!
!
!
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
!
直角三角形的性质和判定!
"
"! "
!前置诊断"检测你的基础#助力新课学习
!
!!
若%
,0)
&
&
',
&
02,0-
!则
-
的值为 %
!!
&
*!2 ,!9$- .!62 /!$-
"!
已知一个正方形的面积为
$&
!则它的边长为 %
!!
&
*!- ,!&槡+ .!+槡& /!)
#!
已知直角三角形的两条直角边长分别为
+
和
)
!则这个三角形的面积为 %
!!
&
*!- ,!+! .!$& /!3
!前置巩固"如果你没有全部正确#务必回顾复习
!
$!
完全平方公式"%
*9-
&
&
'*
&
9&*-0-
&
!
&!
正数有一个正的平方根!这个平方根叫做算术平方根
!
+!
直角三角形的面积等于两条直角边的积的一半
!
!!
直角三角形中#三边之间有特殊的数量关系吗$ 今天我们来探究直角三角形三边之
间的数量关系
!
!!
勾股定理"直角三角形两直角边
*
#
-
的平方和#等于斜边
.
的平方
%
$
&这一定理只对直角三角形适用!对锐角三角形和钝角三角形不适用
!
利用公式
时!要分清是直角边还是斜边
!
%
&
&直角三角形中!已知任意两边!可以求出第三边
!*
&
0-
&
'.
&
!可化为"
*
&
'.
&
6-
&
!
-
&
'.
&
6*
&
%
*
!
-
为直角边!
.
为斜边&
!
%
+
&这一定理把角度关系转化为数量关系!是转化思想的一个典范
!
"!
勾股定理可以用图形的面积证明
体现了数形结合的数学思想!把直角三角形这个(形*与三边关系这一(数*结合起
来
!
教科书中给出了勾股定理的一种证明方法!历史上有许多人对勾股定理进行了研究!
给出了勾股定理的一些证明方法!感兴趣的同学可以自行查阅有关资料
!
#!
勾股定理又称商高定理!毕达哥拉斯定理!百牛定理
例
!
!
勾股定理是(人类最伟大的十个科学发现之一*
!
我国对勾股定理的证明是由汉
代的赵爽在注解,周髀算经-时给出的!他用来证明勾股定理的图案被称为(赵爽弦图*
!&""&
年在北京召开的国际数学大会就是选它作为会徽
!
下列图案中是(赵爽弦图*的是 %
!!
&
* , . /
解"(赵爽弦图*是由
)
个全等的直角三角形和中间的小正方形拼成的一个大正方
形!故选
,!
例
"
!
在
45
"
#$%
中!
#
%'1"(
!
*
!
-
!
.
分别表示
#
#
!
#
$
!
#
%
的对边
!
图
$!& $ $
!!!!!!图
$!& $ &
%
$
&如图
$!& $ $
!已知"
*'3
!
.'&!
!求
-
'
%
&
&如图
$!& $ &
!已知"
.'&!
!
*%-')%+
!求
*
!
-!
解"%
$
&
-' &!
&
63槡 &'&)!
%
&
&设
*'),
!
-'+,!
由题意可得
.'
%
),
&
&
0
%
+,
&槡 &'!,'&!!
解得
,'!!
所以
*'&"
!
-'$!!
注意"本题考查的是勾股定理!如果直角三角形的三边长分别为
*
!
-
!
.
!则满足
*
&
0
-
&
'.
&
!
!!
在
45
"
#$%
中!有两边的长分别为
+
和
)
!则第三边的长为 %
!!
&
*! ,!槡3 .!或槡3 /!或槡$$
"!
已知
"
#$%
的三边长为
*
!
-
!
.
!且满足
*0-'$"
!
*-'$2
!
.'2
!则此三角形为
!!!!
三
角形
!
#!
如图
$!& $ +
!在等腰
"
#$%
中!
#$'#%
!
#&
是底边
$%
上的高!若
#$'!8#
!
!
图
$!& $ +
$%'-8#
!求
#&
的长
!
$!
勾股定理是刻画直角三角形三边关系的重要定理!一定要熟记
!
在直角三角形中!
已知任意两边!可以求出第三边
!
&!
利用勾股定理解题时!要分清直角边和斜边!题目没有指明斜边时!要分类讨论
!
!!
在
45
"
#$%
中!
#
%'1"(
!若
#$'$+
!
$%'!
!则
#%
的长为 %
!!
&
*! ,!2 .!$& /!$2
"!
在
45
"
#$%
中!有两边的长分别
!
和
$&
!则第三边长为
!!!!
!
#!
直角三角形的斜边长为
!8#
!两直角边长之比为
+%)
!那么这个直角三角形的周长为
!!!!
!
$!
如图
$!& $ )
!在
45
"
#$%
中!
#
#%$'1"(
!以它的各边为边向外作三个正方形!面
积分别为
"
$
!
"
&
!
"
+
!已知
"
$
'-
!
"
&
'2
!则
"
+
'
!!!!
!
图
$!& $ )
%!
如图
$!& $ !
!在
45
"
#$%
中!
#
%'1"(
!
$%'-
!
#%'2
!
#$
的垂直平分线
&'
交
#$
于点
&
!交
#%
于点
'
!连接
$'!
%
$
&求
#&
的长'
%
&
&求
#'
的长
!
!
图
$!& $ !
!!"
!
直角三角形的性质和判定!
"
"!
"
"
!前置诊断"检测你的基础#助力新课学习
!
!!
在
45
"
#$%
中!
#
%'1"(
!
#$'$"8#
!
#%'28#
!则
$%
长为 %
!!
&
*!-8# ,!$)8# .!$&8# /!$28#
"!
在
45
"
#$%
中!
#
$'1"(
!
#$'!
!
$%'$&
!则
#%
的长为 %
!!
&
*!3 ,!槡$$1 .!$+ /!$2
#!
在
45
"
#$%
中!有两边的长分别为
+
和
!
!则第三边的长为 %
!!
&
*!) ,!槡&1 .!)或槡&1 /!)或槡+)
!前置巩固"如果你没有全部正确#务必回顾复习
!
$!
勾股定理"直角三角形的两条直角边的平方和!等于斜边的平方
!
&!
全等三角形的性质"全等三角形的对应边相等!对应角相等
!
!!
我们已经学习了勾股定理#运用勾股定理可以解决一些几何问题和实际问题
!
!!
利用勾股定理解决实际问题!要善于从实际问题中抽象出几何模型!再画出几何
图形!从而把实际问题转化为数学问题
!
"!
构造直角三角形模型后!确定斜边$直角边'不是直角三角形的要通过作垂线%或
平行线&构造出直角三角形
!
#!
在实际问题中!常常默认电线杆$旗杆$大树$建筑物等垂直于地面
!
$!
求解方位角的问题时!东西方向和南北方向在平面中恰好垂直!因而常利用这一
垂直关系来建立直角三角形
!
%!
要注意用转化$数形结合$方程等思想来解决相关问题
!
例
!
!
数学综合实验课上!同学们在测量学校旗杆的高度时发现"将旗杆顶端升旗用的
绳子垂到地面还多
&#
'当把绳子的下端拉开
2#
后!下端刚好接触地面!如图
$!& & $!
根据以上数据!同学们准确求出了旗杆的高度!你知道他们是如何计算出来的吗#
图
$!& & $
解"设旗杆高
,#
!则绳子长为%
,0&
&
#!
:
旗杆垂直于地面!
;
旗杆$绳子与地面构成直角三角形
!
由题意列式为
,
&
02
&
'
%
,0&
&
&
!解得
,'$!!
;
旗杆的高度为
$!#!
注意"由题可知!旗杆$绳子与地面构成直角三角形!根据题中数据!用勾股定理即可
求解
!
本题考查的是勾股定理的应用!根据题意找出直角三角形是解答此题的关键
!
!
图
$!& & &
例
"
!
如图
$!& & &
!甲乙两船从港口
#
同时出发!甲船以
$-
海里+
7
的速度向北偏东
)"(
方向航行!乙船向南偏东
!"(
方向航
行!
+7
后!甲船到达
%
岛!乙船到达
$
岛
!
若
%
!
$
两岛相距
$"&
海里!
问乙船的航速是多少#
解"
:
#
$#%'$2"(6)"(6!"('1"(
!
;
"
#$%
是直角三角形!
;#%
&
0#$
&
'$%
&
!
:#%'$-<+')2
%海里&!
$%'$"&
海里!
;#$' $%
&
6#%槡 &' $"&&6)2槡 &'1"%海里&!
:
乙船航行时间为
+7
!
;
乙船的航速为
1"=+'+"
%海里+
7
&
!
答"乙船的航速是
+"
海里+
7!
注意"先根据方位角的定义证得
"
#$%
是直角三角形!再求出
#%
的长度!根据勾股
定理求得
#$
的长!然后根据乙船的航行时间即可解题
!
本题考查了方位角问题及勾股
定理的应用!理解方位角的定义证得
"
#$%
是直角三角形是解答本题的关键
!
图
$!& & +
!
!!
一云梯
#$
长
&!#
!如图
$!& & +
所示斜靠在一面墙上!云梯
底端离墙
3#
!如果云梯的顶端下滑了
)#
!那么它的底端在水
平方向滑动
$$/
的长是 %
!!
&
*!$"#
,!2#
.!-#
/!)#
!
图
$!& & )
"!
老师要求同学们设计一个测量某池塘两端
#
!
$
距离的方案!王兵设
计的方案如下"如图
$!& & )
!在池塘外选一点
%
!测得
#
%#$'1"(
!
#
%'+"(
!
#%'+-#
!则可知
#$
的距离为 %
!!
&
*! 槡$1 +# ,!$1#
.! 槡$& +# /! 槡$& &#
#!
如图
$!& & !
是一株美丽的勾股树!其中所有的四边形都是正方形!所有的三角形都
是直角三角形
!
若正方形
#
!
$
!
%
!
&
的边长分别是
+
!!
&
!
+
!则最大正方形
'
的面积是
%
!!
&
图
$!& & !
*!$+ ,!&- .!+) /!)3
$!
如图
$!& & -
!甲轮船以
&)
海里+
7
的速度离开港口
+
向东南方向航行!乙轮船在同
时同地向西南方向航行!已知它们离开港口
+
半小时后分别到达
$
!
#
两点!且相距
$!
海里!问乙轮船每小时航行多少海里#
!
图
$!& & -
$!
利用勾股定理解决实际问题!要抽象出几何图形!找到直角三角形!同时注意问题
中变与不变的线段长度
!
&!
还可利用勾股定理求由几个正方形或圆构成的图形的面积
!
!
图
$!& & 3
!!
如图
$!& & 3
!一棵大树在离地面
-#
高的
$
处断裂!树顶
#
落在离树底部
%
的
2#
处!则大树断裂之前的高度为 %
!!
&
*!$-# ,!$!#
.!&)# /!&$#
"!
如图
$!& & 2
!公路
#%
!
$%
互相垂直!公路
#$
的中点
0
与点
%
被湖隔开!若测得
#%'$&>#
!
$%'$->#
!则
0
!
%
两点之间的距离为 %
!!
&
*!$+># ,!$&># .!$$># /!$">#
图
$!& & 2
!!!!!!! 图
$!& & 1
#!
如图
$!& & 1
!在
45
"
#$%
中!
#
#%$'1"(
!则三个半圆的面积关系是 %
!!
&
*!"
$
0"
&
&
"
+
,!"
$
0"
&
'"
+
.!"
$
0"
&
'
"
+
/!"
&
$
0"
&
&
'"
&
+
$!
如图
$!& & $"
!一艘船由
#
港沿北偏东
-"(
方向航行
$">#
至
$
港!然后再沿北偏
西
+"(
方向航行
$">#
至
%
港
!
%
$
&求
#
!
%
两港之间的距离%结果精确到
"!$>#
!参考数据"槡&
%
$!)$)
!槡+
%
$!3+&
&'
%
&
&确定
%
港在
#
港的什么方向
!
!
图
$!& & $"
%!
甲同学在拼图探索活动中发现!用
)
个形状大小完全相同的直角三角形%直角边长分
别为
*
!
-
!斜边长为
.
&!可以拼成如图
$!& & $$
所示的正方形!并由此得出了关于
*
&
!
-
&
!
.
&的一个等式
!
图
$!& & $$
!!!! 图
$!& & $&
%
$
&请你写出这一结论"
!!!!
!并给出验证过程'
%
&
&试用上述结论解决问题"如图
$!& & $&
!
)
是
45
"
#$%
斜边
#$
上的一个动点!
已知
#%'!
!
#$'$+
!求
)%
的最小值
!
!
!!"
!
直角三角形的性质和判定!
"
"!
#
"
!前置诊断"检测你的基础#助力新课学习
!
!!
若等腰三角形的腰长为
$+
!底边长为
$"
!则底边上的高为 %
!!
&
*!- ,!3 .!1 /!$&
"!
下列命题的逆命题是假命题的是 %
!!
&
*!
直角三角形中的两个锐角互余
,!
直角三角形斜边上的中线等于斜边的一半
.!
两个全等三角形的对应角相等
/!
两个全等三角形的对应边相等
#!
请写出(直角三角形的两条直角边
*
$
-
和斜边
.
满足关系式"
*
&
0-
&
'.
&
*的逆命题"
!!!!!!!!!!!!!!!! !
!
!前置巩固"如果你没有全部正确#务必回顾复习
!
$!
勾股定理"直角三角形的两条直角边
*
!
-
的平方和!等于斜边
.
的平方
!
&!
互逆命题"对于两个命题!如果一个命题的条件和结论分别是另一个命题的结论和
条件!我们把这样的两个命题称为互逆命题!其中一个叫作原命题!另一个叫作逆命题
!
!!
我们知道%直角三角形两直角边的平方和#等于斜边的平方&#那么反过来#已知一个
三角形有两边的平方和等于第三边的平方#能判定这个三角形是直角三角形吗$
!!
勾股定理的逆定理"如果三角形的三条边长
*
!
-
!
.
满足关系式"
*
&
0-
&
'.
&
!那么
这个三角形是直角三角形
!
勾股定理的逆定理是判定一个三角形为直角三角形的方法!不能叙述为(斜边的平
方等于两条直角边的平方和*
!
在判定一个三角形为直角三角形之前!不能说哪条边为斜
边!哪条边为直角边
!
这一定理把线段长度关系转化为角度关系!是由(数*到(形*!体现了数形结合的转
化思想
!
"!
勾股数"满足
*
&
0-
&
'.
&的三个正整数称为勾股数
!
勾股数是一组正整数
!
以一组勾股数的长度为三边的三角形!是一个直角三角形
!
常见的勾股数有"
+
!
)
!'
!
!
$&
!
$+
'
3
!
&)
!
&!
'
2
!
$!
!
$3
'
1
!
)"
!
)$
等
!
对于任何一组勾股
数!将各数乘相同整教!则能得到另一组勾股数
!
如"由
+
!
)
!是一组勾股数!可得到
$2
!
&)
!
+"
也是勾股数
!
!
图
$!& + $
例
!
!
如图
$!& + $
!正方形网格中每个小方格的边长为
$
!且点
#
!
$
!
%
均为格点!通过计算判断
"
#$%
的形状
!
解"由勾股定理得
#%
&
')
&
0&
&
'&"
!
$%
&
'&
&
0$
&
'!
!
#$
&
'
+
&
0)
&
'&!
!
;#%
&
0$%
&
'#$
&
!
;
"
#$%
是直角三角形
!
例
"
!
如图
$!& + &
!在
"
#$%
中!
$&
$
#%
!
#$'&"
!
$%'$!
!
%&'1!
!
图
$!& + &
%
$
&求
#%
的长'
%
&
&判断
"
#$%
的形状并证明
!
解"%
$
&在
"
#$%
中!
:$&
$
#%
!
#$'&"
!
$%'$!
!
&%'1
!
;$&' $!
&
61槡 &'$&!
;#&' &"
&
6$&槡 &'$-!
;#%'#&0&%'$-01'&!!
%
&
&
:#%'&!
!
$%'$!
!
#$'&"
!
&"
&
0$!
&
'&!
&
!
;
"
#$%
是直角三角形
!
!!
下列四组线段!可以构成直角三角形的是 %
!!
&
*!)
!!
- ,!
!
$&
!
$+ .!&
!
+
!
) /!$
!槡&!+
"!
适合下列条件的
"
#$%
中!直角三角形的个数为 %
!!
&
%
$
&
*'-
!
#
#')!(
' %
&
&
#
#'+&(
!
#
$'!2(
'
%
+
&
*'-
!
-'2
!
.'$"
' %
)
&
*'-
&
!
-'2
&
!
.'$"
&
!
*!$ ,!& .!+ /!)
#!
已知
*
!
-
!
.
是
"
#$%
的三边长!且满足关系式
.
&
6*
&
6-槡 &0 *6- '"!则
"
#$%
的
形状为
!!!!!!
!
$!
如图
$!& + +
!在
"
#$%
中!已知
#$'#%'$+8#
!
&
是
#$
上一点!且
%&'
$&8#
!
$&'28#!
!
图
$!& + +
%
$
&求证"
"
#&%
是直角三角形'
%
&
&求
$%
的长
!
$!
用勾股定理的逆定理判定直角三角形的步骤"
%
$
&先找出最长的一条边
.
!算出
.
&
!
%
&
&计算两条较短边
*
!
-
的平方和
!
%
+
&如有
*
&
0-
&
'.
&
!则可判定这个三角形是直角三角形'否则不能判定
!
如果不能确
定最长的边!则需分类讨论
!
&!
应用勾股定理及其逆定理时应分清条件和结论
!
!!
在
"
#$%
中!
#$'$&8#
!
#%'18#
!
$%'$!8#
!则
"
#$%
的面积
"
"
#$%
是%
!!
&
*!$"28#
&
,!)8#
&
.!$2"8#
&
/!1"8#
&
"!
已知
*槡6$&0 -% &6! & 0 .6$+ '"!则以*!-!.为三边的三角形的形状是
!!!!!!!!
!
#!
如图
$!& + )
!在
)<+
的正方形网格中!每个小正方形的边长都为
$!
%
$
&线段
#$
的长为
!!!!
'
%
&
&在图中作出线段
'(
!使得
'(
的长为槡$+!判断#$!%&!'(三条线段能否构成直
角三角形!并说明理由
!
!
图
$!& + )
$!
如图
$!& + !
所示有一块铁皮%图中阴影部分&!测得
#$'+
!
$%')
!
%&'$&
!
#&'
$+
!
#
$'1"(!
求阴影部分的面积
!
!
图
$!& + !
%!
如图
$!& + -
!在四边形
#$%&
中!
#$'$%'%&'#&')
!
#
&#$'
#
$'
#
%'
#
&'1"(
!
'
!
(
分别是
$%
和
%&
边上的点!且
%''
$
)
$%
!
(
为
%&
的中点!问
"
#'(
!
图
$!& + -
是什么三角形# 并说明理由
!
!!"
"#$#%&'()
*+
!
"
"!"
!前置诊断"
!!!
!
"!"
!
#!&
!变式训练"
!!*
"!
直角
!
!
(8)
"
(
-'+
(
4(5'$-3,
#
.*
(
-3,
#
1(
(
8)
(
-*
(
!
1
#
"$%
是直角三角形
!
#!,67
!效果检测"
!!*
!
"!'#
或槡''2!#!'(67!
$!',
!
.
"
"%$-2+%
#
+
'
-3
#
+
(
-$
#
1"%
(
-3
#
$%
(
-$
#
1"$
(
-"%
(
8$%
(
-',!
1+
#
-',!
%!
!
'
"在
/0
#
"$%
中#
.
"
%-2+%
#
$%-3
#
"%-$
#
1"$- 3
(
8$槡 (-'+!
.#,
垂直平分
"$
#
1"#-$#-)!
!
(
"
.#,
垂直平分
"$
#
1$,-",!
设
,%--
#则
",-$,-$4-!
故
3
(
8-
(
-
!
$4-
"
(
!
解得
--
9
,
!
1",-$4
9
,
-
()
,
!
!!"
"#$#%&'()
*+
!
"
"!
"
"
!前置诊断"
!!&
!
"!*
!
#!!
!
!变式训练"
!!"
!
由题意可得$
"$-()7
#
'$-97
#
则
'"- "$
(
4'$槡 (- ()(49槡 (-(,!7"!
当云梯的顶端下滑了
,7
#则
".'-(,4,-
(+
!
7
"
!
故
'$.- ()
(
4(+槡 (-')!7"#
则
$$.-'$.4'$-$7!
故选
"!
"!*
!
.
"
%"$-2+%
#
"
%-#+%
#
"%-#37
#
设
"$--7
#则
$%-(-7!
1"%
(
8"$
(
-$%
(
#
即
#3
(
8-
(
-
!
(-
"
(
!
解得
--'(槡#!故选*!
#!!
!
由勾股定理得#正方形
/
的面积
-
正方形
"
的面积
8
正方形
$
的面积
-#
(
8)
(
-#,!
同理#正方形
0
的面积
-
正方形
%
的面积
8
正
方形
#
的面积
-(
(
8#
(
-'#!
1
正方形
,
的面积
-
正方形
/
的面积
8
正方
形
0
的面积
-,9!
故选
!!
$!.
甲轮船向东南方向航行#乙轮船向西南方向
航行#
1"'
$
$'!
.
甲轮船以
(,
海里%
:
的速度航行了半小时#
1'$-(,5+!)-'(
!海里"
!
又
."$-')
海里#
1
在
/0
#
"'$
中#
"' - "$
(
4'$槡 ( -
')
(
4'(槡 (-2!海里"#
1
乙轮船每小时航行
2;+!)-'$
!海里"
!
!效果检测"
!!&
!
"!!
#!"
!
.
"
"%$-2+%
#
1"%
(
8$%
(
-"$
(
!
.+
'
-
'
(
!
"%
! "
(
(
-
!
&
"%
(
$
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
#
+
(
-
'
(
!
$%
! "
(
(
-
!
&
$%
(
$
#
+
#
-
'
(
!
"$
! "
(
(
-
!
&
"$
(
$
#
1+
'
8+
(
-
!
$
!
"%
(
8$%
(
"
-
!
$
"$
(
-+
#
!
即
+
'
8+
(
-+
#
!
故选
"!
$!
!
'
"由题意可得
"
&$%-#+%
#
"
1"$-3+%!
1
"
%$2-3+%
#
"
$"3-#+%
#
1
"
"$2-#+%
#
1
"
"$%-2+%!
."$-$%-'+<7
#
1"%- "$
(
8$%槡 ( 槡-'+ ('',!'!<7"!
故
"
#
%
两港之间的距离约为
',!'<7!
!
(
"由!
'
"知#
#
"$%
为等腰直角三角形#
1
"
$"%-,)%
#
1
"
%"1-3+%4,)%-')%!
1%
港在
"
港的北偏东
')%
方向上
!
%!
!
'
"结论$
(
(
8)
(
-*
(
!
证明$
.
阴影部分的面积
-,5
'
(
()-(()
#
阴影部分的面积
-
!
(8)
"
(
4*
(
#
1
!
(8)
"
(
4*
(
-(()
#即
(
(
8)
(
-*
(
!
!
(
"在
/0
#
"$%
中#
"%-)
#
"$-'#
#
1)
(
8$%
(
-'#
(
#
解得
$%-'(!
当
%&
$
"$
时#
&%
最短#
此时'
(
$%5"%-
'
(
"$5&%
#
即
&%-
)5'(
'#
-
3+
'#
#
1&%
的最小值为3+
'#
!
!!"
"#$#%&'()
*+
!
"
"!
#
"
!前置诊断"
!!!
!
"!*
!
如果一个命题的条件和结论分别是另一个
命题的结论和条件#那么这两个命题叫作互逆
命题
!
选项
*
的逆命题是$对应角相等的两个三
角形是全等三角形#显然是假命题
=
故选
*=
#!
如果三角形的三条边长
(
#
)
#
*
满足关系式$
(
(
8)
(
-*
(
#那么这个三角形是直角三角形
!变式训练"
!!"
"!*
!
直角三角形是!
'
"!
(
"!
#
"#故选
*!
#!
等腰直角三角形
$!
!
'
"
."$-'#67
#
$#-$67
#
1"#-"$4$#-)67!
."%-'#67
#
%#-'(67
#
1"#
(
8%#
(
-"%
(
#
1
"
"#%-2+%
#
故
#
"#%
是直角三角形
!
!
(
"在
/0
#
$#%
中#
"
$#%-'$+%42+%-2+%
#
$#-$67
#
%#-'(67
#
由勾股定理得
$%- $#
(
8%#槡 (- $(8'(槡 (-
,槡'#!67"!
!效果检测"
!!"
!
"!
直角三角形
#!
!
'
"槡)
!
(
"如图#
,/- #
(
8(槡 (-槡'##%#- ((8(槡 (-
(槡(!
.%#
(
8"$
(
-$8)-'#
#
,/
(
-'#
#
1%#
(
8"$
(
-,/
(
#
1"$
#
%#
#
,/
三条线段可以构成直角三角形
!
$!
连接
"%!
在
#
"$%
中#
.
"
$-2+%
#
"$-#
#
$%-,
#
1"%- #
(
8,槡 (-)!
.%#-'(
#
"#-'#
#
"%-)
#
1"%
(
8%#
(
-"#
(
#
1
#
"%#
是直角三角形
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
#
1+
阴影
-+
#
"%#
4+
#
"$%
-
'
(
5)5'(4
'
(
5
#5,-#+43-(,!
%!
直角三角形
!
理由如下$
."$-$%-%#-"#-,
#
%,-
'
,
$%
#
1,%-'
#
$,-#!
./
为
%#
的中点#
1#/-/%-(!
.
"
#"$-
"
$-
"
%-
"
#-2+%
#
1,/- (
(
8'槡 ( 槡- )#
"/- ,
(
8(槡 ( 槡- (+#
",- ,
(
8#槡 (-)#
1",
(
-,/
(
8"/
(
!
1
#
",/
是直角三角形
!
! ! ! !
!
!
!
!
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
