2020春北师大版七年级数学下册 4.2图形的全等同步测试(含答案)
文档属性
| 名称 | 2020春北师大版七年级数学下册 4.2图形的全等同步测试(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 819.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-28 17:11:37 | ||
图片预览




文档简介
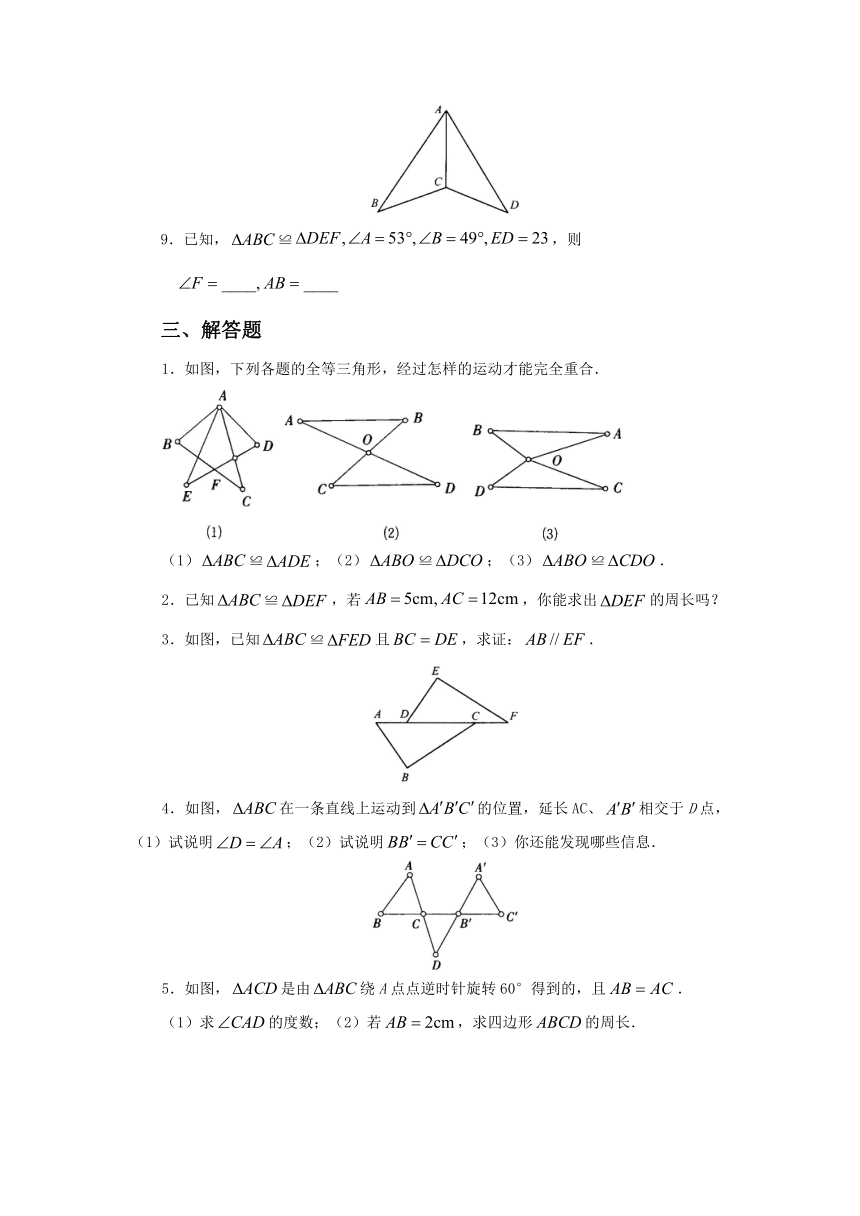
2020春北师大版七下数学4.2图形的全等同步测试1
1.观察如图5—34所示的各个图形,指出其中的全等图形.
2.如图5—35所示,判断各组中的两个图形是否是全等图形.
3.如图5—36所示,试判断图中的两个图形是否全等;若不全等,请说明理由;若全等,请说明怎样做才能使它们重合,
4.画一个三角形,再画一个与其全等的图形.
5.画一个长方形,再用尺规作一个图形,使它们成为全等图形.
6.在一个梯形上画出你喜爱的图形,然后复制6个并拼成一个较大的图案.
7.用相同的长方形(长与宽的比为2:1)尽量拼成几种不同的图案.
8.如图5—37所示,把梯形分割成两对全等的图形.
9.按下列步骤设计图案.
①画一个ΔABC,其中AB=AC;
②去掉两个全等的等边三角形l,2,并且BD=CD′;
③将三角形1,2分别放在3,4的位置,其中AE=BD=AE′.
参考答案
1.解:①和⑥,②和⑤,③和⑧分别为全等的图形.
2.解:甲不是,乙是.
3.解:两个图形全等;折叠能使它们重合. 4.略. 5.略. 6.略. 7.略.
8.解;如图5—38所示.
9.解:如图54—39所示.
2020春北师大版七下数学4.2图形的全等同步测试2
一、选择题
1.已知≌,且,则( )
A.50° B.100° C.30° D.50°或100°或30°
2.已知≌,且,则=( )
A.3cm B.4cm C.5cm D.以上都不对
3.若两个三角形( ),则一个三角形和另一个三角形全等.
A.面积相等 B.周长相等
C.对应边相等,对应角相等 D.以上都不对
4.如果D是中BC边上一点,并且≌,则ΔABC是( )
A.锐角三角形 B.钝角三角形
C.直角三角形 D.等腰三角形
二、填空题
1.如图,若把沿着直线BC移动,它就和重合,那么和_________;对应相等的边分别是_________、_________、_________;对应相等的角分别是_________、__________、___________.
2.如图,≌,则对应边有__________,对应角有________.
3.如图,≌,则的对应角是___________,BD的对应边是__________.
4.已知:≌,,cm,则.
5.如果≌,cm,则cm.
6.若≌,的周长为32cm,,则cm,cm,cm.
7.如图,沿BC折叠,若A与D重合,则_____,其对应边为 ,对应角为 .
8.如图,≌,写出相等的角和边
9.已知,≌,则
三、解答题
1.如图,下列各题的全等三角形,经过怎样的运动才能完全重合.
(1)≌;(2)≌;(3)≌.
2.已知≌,若,你能求出的周长吗?
3.如图,已知≌且,求证:.
4.如图,在一条直线上运动到的位置,延长AC、相交于D点,(1)试说明;(2)试说明;(3)你还能发现哪些信息.
5.如图,是由绕A点点逆时针旋转60°得到的,且.
(1)求的度数;(2)若,求四边形的周长.
参考答案
一、选择题
1.C 2.A 3.C 4.D
二、填空题
1.全等;
2.AC和AB,AE和AF,BE和CF;和
3.
4.70°,10cm
5.47°,25
6.9,12,11
7.≌ AB与DB、AC与DC、BC与BC
与与与
8.边:
角:
9.78° 23
三、解答题
1.(1)把其中一个三角形沿AF所在的直线对折过去 (2)把其中一个三角形绕O点旋转180° (3)把其中一个三角形沿的角平分线对折过去.
2.周长为25cm
3.≌且
∴
∴
4.提示:≌
5.(1) (2)8cm(提示:≌)
2020春北师大版七下数学4.2图形的全等同步测试3
一、填空题
1.如图,BC平分∠ABD,AB=DB,P为BC上一点,要证∠CAP=∠CDP,应先证_________≌___________;得__________=____________,___________=___________;继而有△PAC≌__________,理由是___________.
2.如图,△ABD≌△ACE,AE=3cm,AC=5cm,则CD=___________cm.
3.若两个图形全等,则其中一个图形可通过平移、__________或__________与另一个三角形完全重合.
4.如图,在△ABC和△DEF,若AB=DE,BE=CF,要使△ABC≌△DEF,还需添加一个条件(只要写出一个就可以)是_________.
5.已知:如图,AB//CD,点O为AC的中点,则图中相等的线段(除OA=OC外)有___________.
6.已知:如图AB//CD,AD//BC,点E,F分别为BD上两点,要使△BCF≌△DAE,还需添加一个条件(只需一个条件)是__________.
7.已知:如图,在△ABC中,AB=AC,∠BAC=∠DAE,D为BE上一点,且∠ADE+∠AEC=180°,则AD=_______.
8.在△ABC与△MNP中,①AB=MN,②BC=NP,③AC=MP,④∠A=∠M,⑤∠B=∠N,⑥∠C=∠P,从这六个条件中任选三个条件,能判定△ABC与△MNP全等的方法共有__________种.
9.铁路上A,B两站(视为直线上两点)相距26km,C,D为两村庄(视为两点),DA⊥AB于点A,CB⊥AB于点B(如图),已知DA=15km,CB=10km,现在要在铁路AB上建设一个土特产品收购站E,使C,D两村到E站的距离相等,则E站应建在距A站________km处.
二、选择题:
10.已知:在△ABC中,AB=AC,∠A=56°,则高BD于BC的夹角为( )
A.28° B.34° C.68° D.62°
11.在ΔABC中,AB=3,AC=4,延长BC至D,使CD=BC,连接AD,则AD的取值范围是( )
A.112.如图,在ΔABC中,∠C=90°,CA=CB,AD平分∠CAB交BC于D,DE⊥AB与点E,且AB=6,则ΔDEB的周长为( )
A.4 B.6 C.8 D.10
13.点P为ΔABC的外角平分线上一点(与C点不重合),则PA+PB与AC+BC的大小关系为( )
A. PA+PB>AC+BC B. PA+PB=AC+BC
C. PA+PB14.已知如图,D是ΔABC边AB上一点,DF交AC与点E,DE=EF,FC//AB,若BD=2,CF=5,则AB=( )
A.1 B.3 C.5 D.7
15.如图,ΔABC是不等边三角形,DE=BC,以D、E为两个顶点作位置不同的三角形,使所作三角形与ΔABC全等,则这样的三角形最多可以画出( )
A.2个 B.4个 C.6个 D.8个
16.如图,在ΔABC中,AB=AC,高BD,CE交与点O,AO交BC于点F,则图中共有全等三角形( )
A.7对 B.6对 C.5对 D.4对
17.如图,在ΔABC中,∠C=90°,AC=BC,AD平分∠BAC交BC于点D,DE⊥AB与点E,若ΔDEB的周长为10cm,则斜边AB的长为( )
A.8cm B.10cm C.12cm D.20cm
18.如图,ΔABC与ΔBDE均为等边三角形,ABA.AE=CD B.AE>CD C.AE19.已知∠P=80°,过不在∠P上一点Q作QM,QN分别垂直与∠P的两边,垂足为M,N则∠Q的度数等于( )
A.10° B.80° C.100° D.80°或100°
三、解答题
20.已知如图,在ΔABC中,∠ACB=90°,AC=BC,AE为BC边上的中线,过点C作CF⊥AE,垂足为F,在直线CD上截取CD=AE.
求证:(1)BD⊥BC;
(2)若AC=12cm,求BD的长.
21.探究题:“有两边及第三边上的高对应相等的两个三角形全等”这一命题是否成立?若成立,请证之;若不成立,请试举一反例,并将命题作适当改正,使之成为一真命题.
22.能够互相重合的多边形叫做全等形,即如果两个多边形对应角相等,那么两个多边形一定全等.但判定两个三角形全等只需三组对应量相等即可,如SAS,SSS等,但如果要判定两个四边形全等仅有四组对应量相等是不够的,必须具备至少五组对应量相等.
(1)请写出两个四边形全等的一种判定方法(五组量对应相等)____________.
(2)如图,简要证明你的判定方法是正确的.
(3)举例说明仅有四边相等的两个四边形不一定全等(画出图形并简要证明).
参考答案
1.ΔABC ΔDBC AC DC ∠ACP ∠DCP ΔPDC SAS
2.2 3.翻转 旋转 4.AC=DF 5.BO=DO,AB=DC 6.BF=DE
7.AE 8.10 9.km
10.A 11.D 12.B 13.A 14.D
15.B 16.A 17.B 18.A 19.D
20.(1)由∠DCB+∠AEC=90°,∠AEC+∠EAC=90°,得∠EAC=∠DCB,在
ΔDBC和ΔECA中,
可知ΔDBC≌ΔECA.有∠ACE=∠DBC=90°,故BD⊥BC.
(2)AC=BC,E是BC的中点,
故,
又ΔDBC≌ΔECA,EC=DB.
由AC=12cm,故EC=6cm,DB=6cm.
21.这个命题是假命题,举一反例即可.
22.(1)∠D=∠D′,AD=A′D′,DC=D′C′,BC=B′C′,AB=A′B′.
(2)连AC
在ΔADC和ΔA′D′C′中,
,
可得ΔADC≌ΔA′D′C′,
故AC=A′C′,
易证:ΔACB≌ΔA′C′B′,
从而获得四边形ABCD和四边形A′B′C′D′对应角,对应边均相等.
即四边形ABCD≌四边形A′B′C′D′.
(3)举一凸四边形和一凹四边形.
1.观察如图5—34所示的各个图形,指出其中的全等图形.
2.如图5—35所示,判断各组中的两个图形是否是全等图形.
3.如图5—36所示,试判断图中的两个图形是否全等;若不全等,请说明理由;若全等,请说明怎样做才能使它们重合,
4.画一个三角形,再画一个与其全等的图形.
5.画一个长方形,再用尺规作一个图形,使它们成为全等图形.
6.在一个梯形上画出你喜爱的图形,然后复制6个并拼成一个较大的图案.
7.用相同的长方形(长与宽的比为2:1)尽量拼成几种不同的图案.
8.如图5—37所示,把梯形分割成两对全等的图形.
9.按下列步骤设计图案.
①画一个ΔABC,其中AB=AC;
②去掉两个全等的等边三角形l,2,并且BD=CD′;
③将三角形1,2分别放在3,4的位置,其中AE=BD=AE′.
参考答案
1.解:①和⑥,②和⑤,③和⑧分别为全等的图形.
2.解:甲不是,乙是.
3.解:两个图形全等;折叠能使它们重合. 4.略. 5.略. 6.略. 7.略.
8.解;如图5—38所示.
9.解:如图54—39所示.
2020春北师大版七下数学4.2图形的全等同步测试2
一、选择题
1.已知≌,且,则( )
A.50° B.100° C.30° D.50°或100°或30°
2.已知≌,且,则=( )
A.3cm B.4cm C.5cm D.以上都不对
3.若两个三角形( ),则一个三角形和另一个三角形全等.
A.面积相等 B.周长相等
C.对应边相等,对应角相等 D.以上都不对
4.如果D是中BC边上一点,并且≌,则ΔABC是( )
A.锐角三角形 B.钝角三角形
C.直角三角形 D.等腰三角形
二、填空题
1.如图,若把沿着直线BC移动,它就和重合,那么和_________;对应相等的边分别是_________、_________、_________;对应相等的角分别是_________、__________、___________.
2.如图,≌,则对应边有__________,对应角有________.
3.如图,≌,则的对应角是___________,BD的对应边是__________.
4.已知:≌,,cm,则.
5.如果≌,cm,则cm.
6.若≌,的周长为32cm,,则cm,cm,cm.
7.如图,沿BC折叠,若A与D重合,则_____,其对应边为 ,对应角为 .
8.如图,≌,写出相等的角和边
9.已知,≌,则
三、解答题
1.如图,下列各题的全等三角形,经过怎样的运动才能完全重合.
(1)≌;(2)≌;(3)≌.
2.已知≌,若,你能求出的周长吗?
3.如图,已知≌且,求证:.
4.如图,在一条直线上运动到的位置,延长AC、相交于D点,(1)试说明;(2)试说明;(3)你还能发现哪些信息.
5.如图,是由绕A点点逆时针旋转60°得到的,且.
(1)求的度数;(2)若,求四边形的周长.
参考答案
一、选择题
1.C 2.A 3.C 4.D
二、填空题
1.全等;
2.AC和AB,AE和AF,BE和CF;和
3.
4.70°,10cm
5.47°,25
6.9,12,11
7.≌ AB与DB、AC与DC、BC与BC
与与与
8.边:
角:
9.78° 23
三、解答题
1.(1)把其中一个三角形沿AF所在的直线对折过去 (2)把其中一个三角形绕O点旋转180° (3)把其中一个三角形沿的角平分线对折过去.
2.周长为25cm
3.≌且
∴
∴
4.提示:≌
5.(1) (2)8cm(提示:≌)
2020春北师大版七下数学4.2图形的全等同步测试3
一、填空题
1.如图,BC平分∠ABD,AB=DB,P为BC上一点,要证∠CAP=∠CDP,应先证_________≌___________;得__________=____________,___________=___________;继而有△PAC≌__________,理由是___________.
2.如图,△ABD≌△ACE,AE=3cm,AC=5cm,则CD=___________cm.
3.若两个图形全等,则其中一个图形可通过平移、__________或__________与另一个三角形完全重合.
4.如图,在△ABC和△DEF,若AB=DE,BE=CF,要使△ABC≌△DEF,还需添加一个条件(只要写出一个就可以)是_________.
5.已知:如图,AB//CD,点O为AC的中点,则图中相等的线段(除OA=OC外)有___________.
6.已知:如图AB//CD,AD//BC,点E,F分别为BD上两点,要使△BCF≌△DAE,还需添加一个条件(只需一个条件)是__________.
7.已知:如图,在△ABC中,AB=AC,∠BAC=∠DAE,D为BE上一点,且∠ADE+∠AEC=180°,则AD=_______.
8.在△ABC与△MNP中,①AB=MN,②BC=NP,③AC=MP,④∠A=∠M,⑤∠B=∠N,⑥∠C=∠P,从这六个条件中任选三个条件,能判定△ABC与△MNP全等的方法共有__________种.
9.铁路上A,B两站(视为直线上两点)相距26km,C,D为两村庄(视为两点),DA⊥AB于点A,CB⊥AB于点B(如图),已知DA=15km,CB=10km,现在要在铁路AB上建设一个土特产品收购站E,使C,D两村到E站的距离相等,则E站应建在距A站________km处.
二、选择题:
10.已知:在△ABC中,AB=AC,∠A=56°,则高BD于BC的夹角为( )
A.28° B.34° C.68° D.62°
11.在ΔABC中,AB=3,AC=4,延长BC至D,使CD=BC,连接AD,则AD的取值范围是( )
A.1
A.4 B.6 C.8 D.10
13.点P为ΔABC的外角平分线上一点(与C点不重合),则PA+PB与AC+BC的大小关系为( )
A. PA+PB>AC+BC B. PA+PB=AC+BC
C. PA+PB
A.1 B.3 C.5 D.7
15.如图,ΔABC是不等边三角形,DE=BC,以D、E为两个顶点作位置不同的三角形,使所作三角形与ΔABC全等,则这样的三角形最多可以画出( )
A.2个 B.4个 C.6个 D.8个
16.如图,在ΔABC中,AB=AC,高BD,CE交与点O,AO交BC于点F,则图中共有全等三角形( )
A.7对 B.6对 C.5对 D.4对
17.如图,在ΔABC中,∠C=90°,AC=BC,AD平分∠BAC交BC于点D,DE⊥AB与点E,若ΔDEB的周长为10cm,则斜边AB的长为( )
A.8cm B.10cm C.12cm D.20cm
18.如图,ΔABC与ΔBDE均为等边三角形,AB
A.10° B.80° C.100° D.80°或100°
三、解答题
20.已知如图,在ΔABC中,∠ACB=90°,AC=BC,AE为BC边上的中线,过点C作CF⊥AE,垂足为F,在直线CD上截取CD=AE.
求证:(1)BD⊥BC;
(2)若AC=12cm,求BD的长.
21.探究题:“有两边及第三边上的高对应相等的两个三角形全等”这一命题是否成立?若成立,请证之;若不成立,请试举一反例,并将命题作适当改正,使之成为一真命题.
22.能够互相重合的多边形叫做全等形,即如果两个多边形对应角相等,那么两个多边形一定全等.但判定两个三角形全等只需三组对应量相等即可,如SAS,SSS等,但如果要判定两个四边形全等仅有四组对应量相等是不够的,必须具备至少五组对应量相等.
(1)请写出两个四边形全等的一种判定方法(五组量对应相等)____________.
(2)如图,简要证明你的判定方法是正确的.
(3)举例说明仅有四边相等的两个四边形不一定全等(画出图形并简要证明).
参考答案
1.ΔABC ΔDBC AC DC ∠ACP ∠DCP ΔPDC SAS
2.2 3.翻转 旋转 4.AC=DF 5.BO=DO,AB=DC 6.BF=DE
7.AE 8.10 9.km
10.A 11.D 12.B 13.A 14.D
15.B 16.A 17.B 18.A 19.D
20.(1)由∠DCB+∠AEC=90°,∠AEC+∠EAC=90°,得∠EAC=∠DCB,在
ΔDBC和ΔECA中,
可知ΔDBC≌ΔECA.有∠ACE=∠DBC=90°,故BD⊥BC.
(2)AC=BC,E是BC的中点,
故,
又ΔDBC≌ΔECA,EC=DB.
由AC=12cm,故EC=6cm,DB=6cm.
21.这个命题是假命题,举一反例即可.
22.(1)∠D=∠D′,AD=A′D′,DC=D′C′,BC=B′C′,AB=A′B′.
(2)连AC
在ΔADC和ΔA′D′C′中,
,
可得ΔADC≌ΔA′D′C′,
故AC=A′C′,
易证:ΔACB≌ΔA′C′B′,
从而获得四边形ABCD和四边形A′B′C′D′对应角,对应边均相等.
即四边形ABCD≌四边形A′B′C′D′.
(3)举一凸四边形和一凹四边形.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
