人教版数学七年级下册9.3 一元一次不等式组课件(共48张PPT)
文档属性
| 名称 | 人教版数学七年级下册9.3 一元一次不等式组课件(共48张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 685.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-29 15:02:42 | ||
图片预览







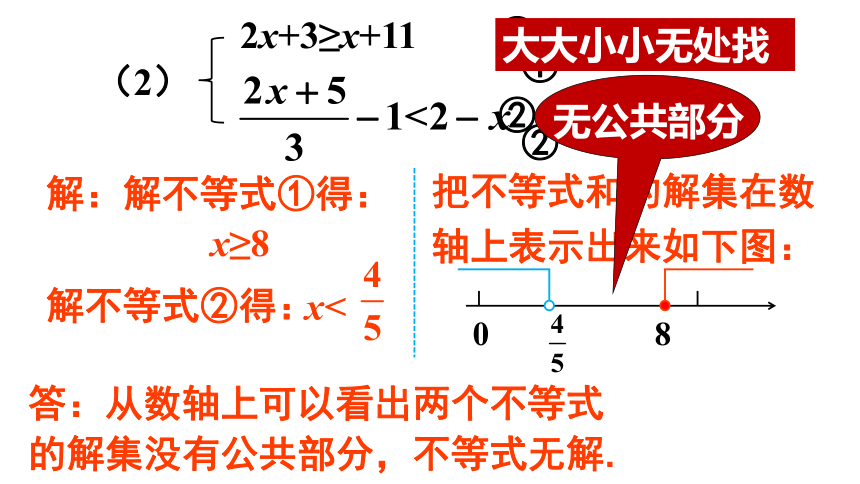
文档简介
课件48张PPT。9.3 一元一次不等式组
情景引入问题 用每分钟可抽30t水的抽水机来抽污水管道里积存的污水,估计积存的污水超过1200t而不足1500t,那么将污水抽完所用时间的范围是什么?1、认识一元一次不等式组及其解的含义.
2、会用数轴找出一元一次不等式组的解 集,能解简单的一元一次不等式组.
学习目标 了解一元一次不等式组的概念,能用数轴找出一元一次不等式组的解集,会解简单的一元一次不等式组.学习重点学习难点 (1)用数形结合的方法,确定一元一次不等式组的解集.
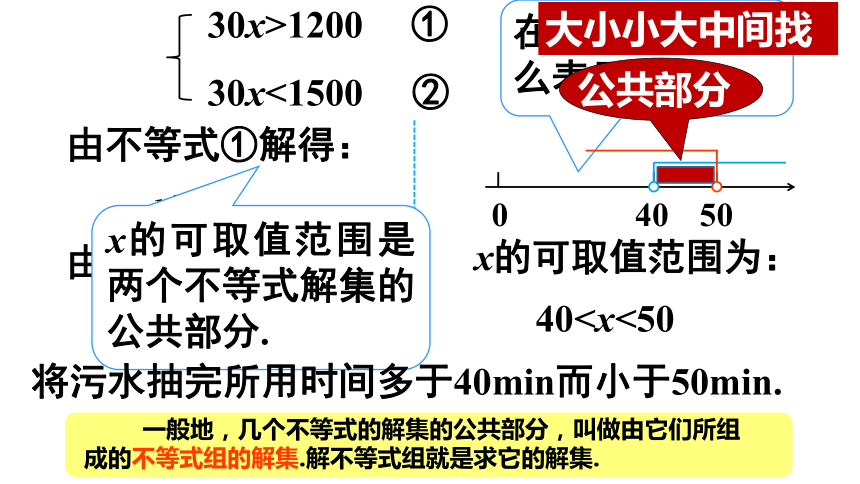
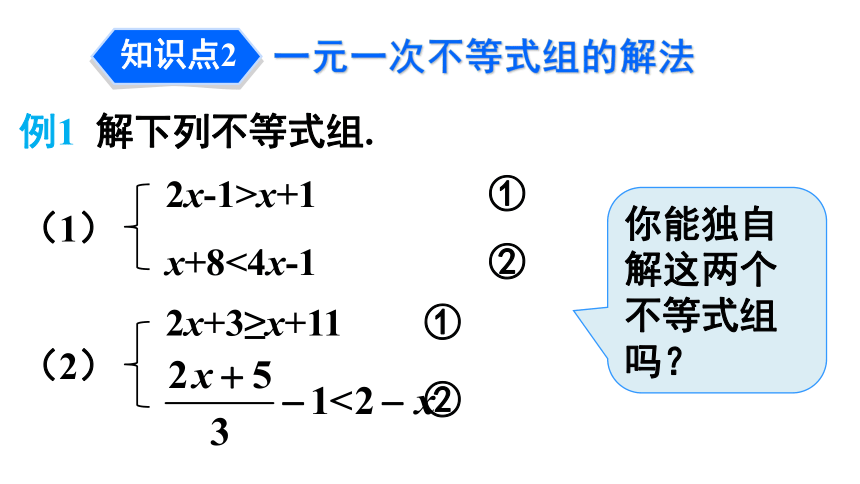
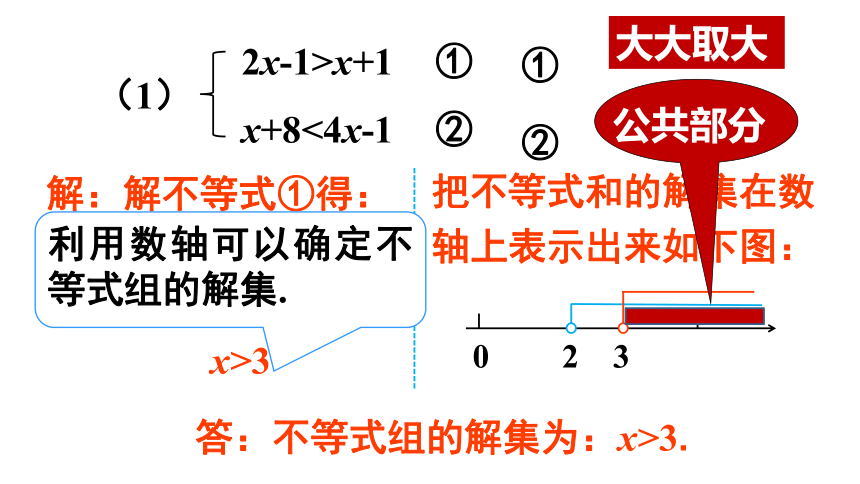
(2)找不等关系列不等式组.一元一次不等式组问题 用每分钟可抽30t水的抽水机来抽污水管道里积存的污水,估计积存的污水超过1200t而不足1500t,那么将污水抽完所用时间的范围是什么?你是怎么想的呢?探究新知要求“将污水抽完所用时间的范围”就必须满足两个条件,即抽出的污水要超过1200t且不足1500t.设用xmin将污水抽完,则x同时满足不等式:30x>1200 ①30x<1500 ②30x>1200 ①30x<1500 ②30x>1200 ①30x<1500 ②在数轴上该怎么表示呢?由不等式①解得:x>40由不等式②解得:x<50x的可取值范围是两个不等式解集的公共部分.x的可取值范围为:402解不等式②得:x>3把不等式和的解集在数轴上表示出来如下图:答:不等式组的解集为:x>3.利用数轴可以确定不等式组的解集.①②大大取大解:解不等式①得:x≥8解不等式②得:把不等式和的解集在数轴上表示出来如下图:答:从数轴上可以看出两个不等式的解集没有公共部分,不等式无解.①②大大小小无处找解不等式组解:解不等式①得:x﹤4解不等式②得:把不等式和的解集在数轴上表示出来如下图:答:从数轴上可以看出两个不等式的解集是x ≤ 2.x≤2小小取小列一元一次不等式解决实际问题的一般步骤:先求出不等式组中各不等式的解集;再求出这些解集的公共部分(可借助数轴).1.解下列不等式组.解:解不等式①得:解不等式②得:x≥1把不等式和的解集在数轴上表示出来如下图:答:这不等式组的解集为:x≥1.解:解不等式①得:解不等式②得:x≥2把不等式和的解集在数轴上表示出来如下图:不等式组无解.x<-6①②解:解不等式①得:解不等式②得:把不等式和的解集在数轴上表示出来如下图:一元一次不等式组的应用例2 x取哪些整数值时,
不等式 5x+2>3(x-1)与 都成立.求出这两个不等式组成的不等式组的解集,解集中的整数就是x可取的整数值.用数轴表示为:答:x可取的整数值是:-2,-1,0,1,2,3,4.①②2、x取哪些正整数值时,不等式x+3>6与2x-1<10都成立.解:不等式x+3>6的解集为 x>3,不等式2x-1<10的解集为 x<5.5,它们解集的公共部分为36与2x-1<10都成立.不能正确确定不等式组的解集解由不等式2x+3<7可得x<2.
由不等式5x-6>9可得x>3.
所以不等式组的解集为2>x>3.错 解误区诊断不能正确确定不等式组的解集正 解由不等式2x+3<7可得x<2.
由不等式5x-6>9可得x>3.
所以不等式组无解.误区诊断错因分析不会确定不等式组的解集,解不等式组要先分别把每个不等式的解集求出来,再借助数轴的直观性,取两个不等式解集的公共部分,不能随意认为“一大一小取中间”,而要具体看两个解集有没有公共部分,公共部分才是它们的解集.应用不等式组的解集时,忽视了等号错 解正 解AB误区诊断错因分析没有对字母a的取值进行分类讨论,而忽略了界点值.此题当中a=2时,不等式组中的两个不等式的解集均为x>2,则不等式组的解集也为x>2.不考虑字母的取值范围错误误区诊断正 解故不等式无解.错因分析对于含字母的解集,要考虑字母的取值范围,若字母的取值范围未知,则应进行分类讨论.基础巩固1. 下列是在数轴上表示的关于x的不等式组的解集,请将各数轴上表示的解集写出来.解集为: .解集为: .解集为: .解集为: .1 A.x>3 B.x<1
C.1<x<2 D.x<1或x>3D4.解下列不等式组:解:解不等式①得:x<4,
解不等式②得:x<2,
∴不等式组的解集为:x<2.解:解不等式①得:x>4,
解不等式②得:x>2,
∴不等式组的解集为:x>4.解:解不等式①得:x<4,
解不等式②得:x>2,
∴不等式组的解集为:24,
解不等式②得:x<2,
∴不等式组无解.5.解下列不等式组:解:解不等式4(x-0.3)<0.5x+5.8得:x<2,∴不等式的解集-4<x<2.又∵x为整数,∴当x取-3,-2,-1,0,1时,不等式4(x-0.3)<0.5x+5.8和3+x> x+1都成立.综合运用7.解下列不等式组:解:解不等式①得 x≤1,
解不等式②得 x<-7,
∴不等式组的解集为 x<-7 .8. 把一些书分给几名同学,如果每人分3本,那么余8本;如果前面的每名同学分5本,那么最后一人就分不到3本,这些书有多少本?共有多少人?解:设共有x人,根据题意,得
解得5<x≤6.5.
∵x为整数,∴x=6.
3x+8=3×6+8=26.
答:这些书有26本,共有6人.拓展延伸解:解不等式5x-1>3(x+1) 得x>2
解不等式 x-1>3- x 得x>2.
解不等式x-1<3x+1 得x>-1.
将三个不等式的解集在数轴上表示出来:
∴三个不等式的解集的公共部分为x>2.一元一次不等式组1.类似于方程组,把这两个不等式合起来,组成一个一元一次不等式组.2.一般地,几个不等式的解集的公共部分,叫做由它们所组成的不等式组的解集.解不等式组就是求它的解集.课堂小结3.列一元一次不等式解决实际问题的一般步骤:先求出不等式组中各不等式的解集;再求出这些解集的公共部分(可借助数轴).课堂小结4.从数轴观察两个不等式组的公共部分的方法:大小小大中间找小小取小大大取大小小大大无处找课堂小结再见
情景引入问题 用每分钟可抽30t水的抽水机来抽污水管道里积存的污水,估计积存的污水超过1200t而不足1500t,那么将污水抽完所用时间的范围是什么?1、认识一元一次不等式组及其解的含义.
2、会用数轴找出一元一次不等式组的解 集,能解简单的一元一次不等式组.
学习目标 了解一元一次不等式组的概念,能用数轴找出一元一次不等式组的解集,会解简单的一元一次不等式组.学习重点学习难点 (1)用数形结合的方法,确定一元一次不等式组的解集.
(2)找不等关系列不等式组.一元一次不等式组问题 用每分钟可抽30t水的抽水机来抽污水管道里积存的污水,估计积存的污水超过1200t而不足1500t,那么将污水抽完所用时间的范围是什么?你是怎么想的呢?探究新知要求“将污水抽完所用时间的范围”就必须满足两个条件,即抽出的污水要超过1200t且不足1500t.设用xmin将污水抽完,则x同时满足不等式:30x>1200 ①30x<1500 ②30x>1200 ①30x<1500 ②30x>1200 ①30x<1500 ②在数轴上该怎么表示呢?由不等式①解得:x>40由不等式②解得:x<50x的可取值范围是两个不等式解集的公共部分.x的可取值范围为:40
不等式 5x+2>3(x-1)与 都成立.求出这两个不等式组成的不等式组的解集,解集中的整数就是x可取的整数值.用数轴表示为:答:x可取的整数值是:-2,-1,0,1,2,3,4.①②2、x取哪些正整数值时,不等式x+3>6与2x-1<10都成立.解:不等式x+3>6的解集为 x>3,不等式2x-1<10的解集为 x<5.5,它们解集的公共部分为3
由不等式5x-6>9可得x>3.
所以不等式组的解集为2>x>3.错 解误区诊断不能正确确定不等式组的解集正 解由不等式2x+3<7可得x<2.
由不等式5x-6>9可得x>3.
所以不等式组无解.误区诊断错因分析不会确定不等式组的解集,解不等式组要先分别把每个不等式的解集求出来,再借助数轴的直观性,取两个不等式解集的公共部分,不能随意认为“一大一小取中间”,而要具体看两个解集有没有公共部分,公共部分才是它们的解集.应用不等式组的解集时,忽视了等号错 解正 解AB误区诊断错因分析没有对字母a的取值进行分类讨论,而忽略了界点值.此题当中a=2时,不等式组中的两个不等式的解集均为x>2,则不等式组的解集也为x>2.不考虑字母的取值范围错误误区诊断正 解故不等式无解.错因分析对于含字母的解集,要考虑字母的取值范围,若字母的取值范围未知,则应进行分类讨论.基础巩固1. 下列是在数轴上表示的关于x的不等式组的解集,请将各数轴上表示的解集写出来.解集为: .解集为: .解集为: .解集为: .1
C.1<x<2 D.x<1或x>3D4.解下列不等式组:解:解不等式①得:x<4,
解不等式②得:x<2,
∴不等式组的解集为:x<2.解:解不等式①得:x>4,
解不等式②得:x>2,
∴不等式组的解集为:x>4.解:解不等式①得:x<4,
解不等式②得:x>2,
∴不等式组的解集为:2
解不等式②得:x<2,
∴不等式组无解.5.解下列不等式组:解:解不等式4(x-0.3)<0.5x+5.8得:x<2,∴不等式的解集-4<x<2.又∵x为整数,∴当x取-3,-2,-1,0,1时,不等式4(x-0.3)<0.5x+5.8和3+x> x+1都成立.综合运用7.解下列不等式组:解:解不等式①得 x≤1,
解不等式②得 x<-7,
∴不等式组的解集为 x<-7 .8. 把一些书分给几名同学,如果每人分3本,那么余8本;如果前面的每名同学分5本,那么最后一人就分不到3本,这些书有多少本?共有多少人?解:设共有x人,根据题意,得
解得5<x≤6.5.
∵x为整数,∴x=6.
3x+8=3×6+8=26.
答:这些书有26本,共有6人.拓展延伸解:解不等式5x-1>3(x+1) 得x>2
解不等式 x-1>3- x 得x>2.
解不等式x-1<3x+1 得x>-1.
将三个不等式的解集在数轴上表示出来:
∴三个不等式的解集的公共部分为x>2.一元一次不等式组1.类似于方程组,把这两个不等式合起来,组成一个一元一次不等式组.2.一般地,几个不等式的解集的公共部分,叫做由它们所组成的不等式组的解集.解不等式组就是求它的解集.课堂小结3.列一元一次不等式解决实际问题的一般步骤:先求出不等式组中各不等式的解集;再求出这些解集的公共部分(可借助数轴).课堂小结4.从数轴观察两个不等式组的公共部分的方法:大小小大中间找小小取小大大取大小小大大无处找课堂小结再见
