6.2.2 向量的减法运算
文档属性
| 名称 | 6.2.2 向量的减法运算 | 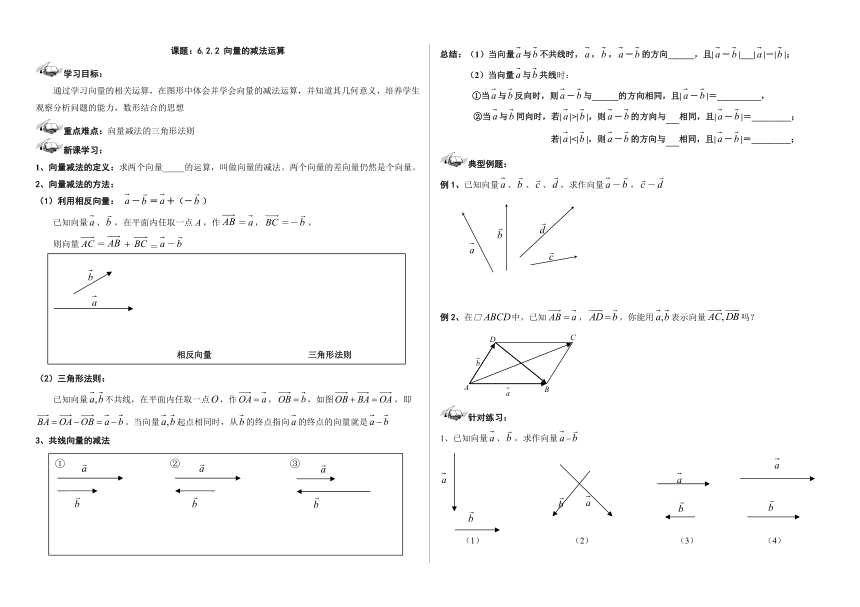 | |
| 格式 | zip | ||
| 文件大小 | 315.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-02 10:29:42 | ||
图片预览

文档简介
课题:6.2.2 向量的减法运算
学习目标:
通过学习向量的相关运算,在图形中体会并学会向量的减法运算,并知道其几何意义,培养学生观察分析问题的能力,数形结合的思想
重点难点:向量减法的三角形法则
新课学习:
1、向量减法的定义:求两个向量_____的运算,叫做向量的减法。两个向量的差向量仍然是个向量。
2、向量减法的方法:
(1)利用相反向量: -=+(-)
已知向量、,在平面内任取一点,作=,=-,
则向量==-
(2)三角形法则:
已知向量不共线,在平面内任取一点,作,,如图,即。当向量起点相同时,从的终点指向的终点的向量就是
3、共线向量的减法
总结:(1)当向量与不共线时,,,-的方向______,且|-|___||-||;
(2)当向量与共线时:
①当与反向时,则-与______的方向相同,且|-|=__________,
②当与同向时,若||>||,则-的方向与___相同,且|-|=_________;
若||<||,则-的方向与___相同,且|-|=_________;
典型例题:
例1、已知向量、、、,求作向量-,-
例2、在□中,已知,,你能用表示向量吗?
针对练习:
1、已知向量、,求作向量
(1) (2) (3) (4)
2、在平行四边形中,已知,,用表示向量
3、化简:
(1)________;(2)__________;(3)_________
(4)________;(5)__________;(6)_________
(7);(8)=_________
(8)=___________
4、已知为平行四边形内一点,,求 (用表示)
课后作业
1、如果表示“向东走10 km”,表示“向西走5 km”,表示“向北走10 km”,表示“向南走5 km”,那么下列向量具有什么意义?
(1)+;______________________ (2)+;______________________
(3)+;______________________ (4)+;______________________
(5)++;__________________ (6)++;______________________
2、一架飞机向北飞行300 km,然后改变方向向西飞行400 km,求飞机飞行的路程及两次位移的合成
3、一艘船垂直于对岸航行,航行速度的大小为15 km/h,同时河水流速的大小为km/h.求船实际航行的速度的大小与方向
4、化简:
(1)++=________ (2)(+)++=________
(3)+++=________ (4)-+-=________
(5)-________ (6)________
(7)=________
5、若向量,,满足++=,那么向量,,的有向线段能构成三角形吗?
6、已知,为两个非零向量,当向量,成什么位置关系时,满足|+|=|-|?
7、填空:
(1)若,满足||=2,||=3,则|+|的最大值为_________,最小值为________
(2)当非零向量,满足___________时,+平分与的夹角.
8、飞机从甲地沿北偏西15°的方向飞行1400 km到达乙地,再从乙地沿南偏东75°的方向飞行1400 km到达丙地,丙地在甲地的___________方向,丙地距甲地_______________
9、(1)如下图,在△ABC中,计算++=_______
(2)如下图,在四边形ABCD中,计算+++=_______
(3)如下图,在n边形A1A2A3…An中,+++…++=______
学习目标:
通过学习向量的相关运算,在图形中体会并学会向量的减法运算,并知道其几何意义,培养学生观察分析问题的能力,数形结合的思想
重点难点:向量减法的三角形法则
新课学习:
1、向量减法的定义:求两个向量_____的运算,叫做向量的减法。两个向量的差向量仍然是个向量。
2、向量减法的方法:
(1)利用相反向量: -=+(-)
已知向量、,在平面内任取一点,作=,=-,
则向量==-
(2)三角形法则:
已知向量不共线,在平面内任取一点,作,,如图,即。当向量起点相同时,从的终点指向的终点的向量就是
3、共线向量的减法
总结:(1)当向量与不共线时,,,-的方向______,且|-|___||-||;
(2)当向量与共线时:
①当与反向时,则-与______的方向相同,且|-|=__________,
②当与同向时,若||>||,则-的方向与___相同,且|-|=_________;
若||<||,则-的方向与___相同,且|-|=_________;
典型例题:
例1、已知向量、、、,求作向量-,-
例2、在□中,已知,,你能用表示向量吗?
针对练习:
1、已知向量、,求作向量
(1) (2) (3) (4)
2、在平行四边形中,已知,,用表示向量
3、化简:
(1)________;(2)__________;(3)_________
(4)________;(5)__________;(6)_________
(7);(8)=_________
(8)=___________
4、已知为平行四边形内一点,,求 (用表示)
课后作业
1、如果表示“向东走10 km”,表示“向西走5 km”,表示“向北走10 km”,表示“向南走5 km”,那么下列向量具有什么意义?
(1)+;______________________ (2)+;______________________
(3)+;______________________ (4)+;______________________
(5)++;__________________ (6)++;______________________
2、一架飞机向北飞行300 km,然后改变方向向西飞行400 km,求飞机飞行的路程及两次位移的合成
3、一艘船垂直于对岸航行,航行速度的大小为15 km/h,同时河水流速的大小为km/h.求船实际航行的速度的大小与方向
4、化简:
(1)++=________ (2)(+)++=________
(3)+++=________ (4)-+-=________
(5)-________ (6)________
(7)=________
5、若向量,,满足++=,那么向量,,的有向线段能构成三角形吗?
6、已知,为两个非零向量,当向量,成什么位置关系时,满足|+|=|-|?
7、填空:
(1)若,满足||=2,||=3,则|+|的最大值为_________,最小值为________
(2)当非零向量,满足___________时,+平分与的夹角.
8、飞机从甲地沿北偏西15°的方向飞行1400 km到达乙地,再从乙地沿南偏东75°的方向飞行1400 km到达丙地,丙地在甲地的___________方向,丙地距甲地_______________
9、(1)如下图,在△ABC中,计算++=_______
(2)如下图,在四边形ABCD中,计算+++=_______
(3)如下图,在n边形A1A2A3…An中,+++…++=______
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
