苏教版高中数学必修一教学讲义,复习补习资料(含知识讲解,巩固练习):09函数的概念和图象及映射的概念(基础)(Word)
文档属性
| 名称 | 苏教版高中数学必修一教学讲义,复习补习资料(含知识讲解,巩固练习):09函数的概念和图象及映射的概念(基础)(Word) |

|
|
| 格式 | zip | ||
| 文件大小 | 210.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-29 00:00:00 | ||
图片预览


文档简介
函数的概念和图象及映射的概念
【学习目标】
了解构成函数的要素有定义域、对应法则、值域,会求一些简单函数的定义域和值域;掌握函数的三种表示方法(图象法、列表法、解析法),会根据不同的需要选择恰当的方法表示函数;了解简单的分段函数,并能简单应用,了解映射的概念,进一步了解函数式非空数集到非空数集的映射。
【要点梳理】
要点一、函数的概念
1.定义
设A、B是非空的数集,如果按照某个确定的对应关系f,使对于集合A中的任意一个数x,在集合B中都有唯一确定的数f(x)和它对应,那么就称f:A→B为从集合A到集合B的一个函数.
记作:y=f(x),xA.
其中,x叫做自变量,x的取值范围A叫做函数的定义域;与x的值相对应的y值叫做函数值,函数值的集合{f(x)|xA}叫做函数的值域.
要点诠释:
(1)A、B集合的非空性;(2)对应关系的存在性、唯一性、确定性;(3)A中元素的无剩余性;(4)B中元素的可剩余性。
2.区间的概念
(1)区间的分类:开区间、闭区间、半开半闭区间;
(2)无穷区间;
(3)区间的数轴表示.
区间表示:
{x|a≤x≤b}=[a,b];
; ;
.
要点二、映射
1.映射定义:
设A、B是两个非空集合,如果按照某个对应法则f,对于集合A中的任何一个元素,在集合B中都有唯一的元素和它对应,这样的对应叫做从A到B的映射;记为f:A→B.
象与原象:如果给定一个从集合A到集合B的映射,那么A中的元素a对应的B中的元素b叫做a的象,a叫做b的原象.
要点诠释:
(1)A中的每一个元素都有象,且唯一;
(2)B中的元素未必有原象,即使有,也未必唯一;
(3)a的象记为f(a).
2.函数与映射的区别与联系:
设A、B是两个非空数集,若f:A→B是从集合A到集合B的映射,这个映射叫做从集合A到集合B的函数,记为y=f(x).
要点诠释:
(1)函数一定是映射,映射不一定是函数;
(2)函数三要素:定义域、值域、对应法则;
(3)B中的元素未必有原象,即使有原象,也未必唯一;
(4)原象集合=定义域,值域=象集合.
要点三、函数的图象
函数的图象是函数关系的一种表示,它是从“形”的方面刻画函数的变化规律。通过函数图象,可以形象地反映函数的性质,利用函数图象既有助于记忆各类初等函数的性质,又可以运用数形结合的方法去解决某些问题。
在中学阶段,画函数图象有两种基本方法:
1、描点法,这种方法要与研究函数性质结合起来,切忌画图的随意性;
2、是图象变换法,它是把常见函数图象与图象变换的知识结合起来,可以研究各种不同函数的性质。在这一部分,首先应熟悉各种变换规则,并且从各个角度将不同变换方法进行对比,从中总结规律,达到熟练掌握的目的。
【典型例题】
类型一、映射的概念
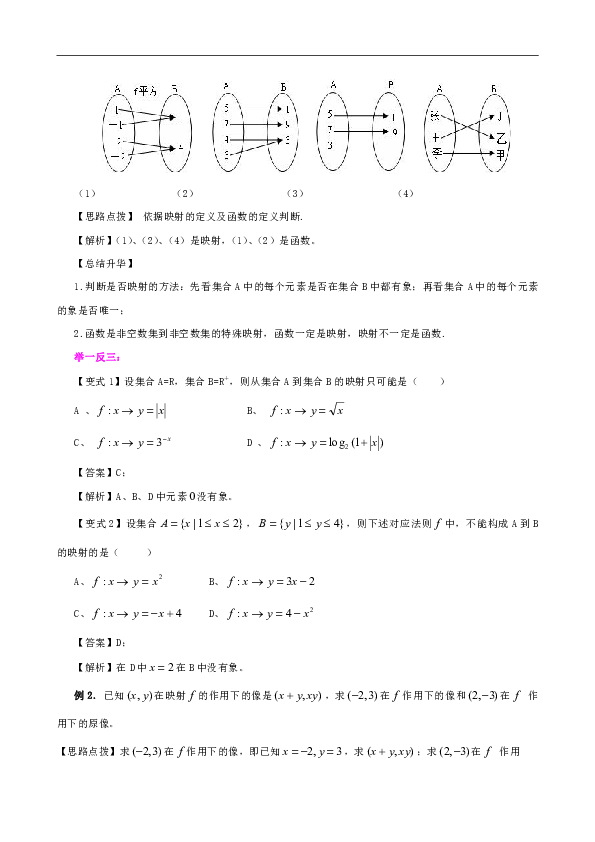
例1.以下对应中,从集合A到集合B的映射有 ;其中 是函数 。
(1) (2) (3) (4)
【思路点拨】 依据映射的定义及函数的定义判断.
【解析】(1)、(2)、(4)是映射,(1)、(2)是函数。
【总结升华】
1.判断是否映射的方法:先看集合A中的每个元素是否在集合B中都有象;再看集合A中的每个元素的象是否唯一;
2.函数是非空数集到非空数集的特殊映射,函数一定是映射,映射不一定是函数.
举一反三:
【变式1】设集合A=R,集合B=R+,则从集合A到集合B的映射只可能是( )
A 、 B、
C、 D 、
【答案】C;
【解析】A、B、D中元素没有象。
【变式2】设集合,,则下述对应法则中,不能构成A到B的映射的是( )
A、 B、
C、 D、
【答案】D;
【解析】在D中在B中没有象。
例2. 已知在映射的作用下的像是,求在作用下的像和在 作用下的原像。
【思路点拨】求在作用下的像,即已知,求;求在 作用下的原像,即为已知,求.
【解析】,
所以在作用下的像是;
或
所以在作用下的原像是.
【总结升华】弄清题意,明白已知是什么,求的又是什么是本题的关键.
举一反三:
【变式】给定映射,点的原象是__________________。
【答案】;
【解析】
类型二、函数的概念
例3.下面各组函数中为相同函数的是( )
A、, B、,
C、, D、,
【思路点拨】判定两个函数相同的方法:当两个函数的三要素相同或者两个函数的对应法则与定义域相同时,两个函数是相同的。
【答案】C;
【解析】A中两函数的定义域不同,的定义域不含;B中两函数的定义域也不同,的定义域为,而的定义域为R;D中的对应法则不同。
【总结升华】对应法则相同与函数的解析式相同是不一样的,对应法则是函数的核心。
举一反三:
【变式】下列各组函数的图象相同的是( )
A、 B、
C、 D、
【答案】D;
【解析】实质为函数相同。A、C中两个函数的定义域不同;B中的对应法则不同。
例4.设,求,;
【思路点拨】 将看作一个整体,换元,求出,再求出.
【解析】设(),则(),
∴ ()
∴(),
().
【总结升华】换元法是常用的求解析式法,注意新元的范围,最后要给出函数的定义域;也可以用 配凑的方法;除以之外,若已知函数类型,还可以利用待定系数法求函数解析式。
举一反三:
【变式1】设,,则 .
【答案】;
【解析】.
类型三、函数的图象
例5.如下图可作为函数的图像的是( )
A B C D
【答案】D;
【解析】作为函数的图像,就看每一个自变量是否对应唯一一个函数值。
例6.把函数y=(x-2)2+2的图象向左平移一个单位,再向上平移一个单位,所得图象对应的函数解析式为_________。
【思路点拨】关于函数图象变换经常会考察这两个内容,给出函数解析式说明变换过程,或给出变换过程写解析式。
【解析】把图象左移一个单位,解析式变为y=(x+1-2)2+2=(x-1)2+2,向上平移一个单位,解析式变为y=[(x-1)2+2]+1=(x-1)2+3.
例7.试讨论方程 |x2-4x+3|=a的解的个数(a∈R).
【解析】本题采用数形结合的方式。
把方程的解的个数看成函数y=|x2-4x+3|和函数y=a的交点个数。
y=|x2-4x+3|的图象是y'=x2-4x+3的图象保留x轴以上部分,将x轴以下部分沿x轴翻折上来形成的图象,而y=a是一条垂直于y轴的直线,如图,由图象可知,a<0时,方程无实解。a=0或a>1时,方程有两个实数解;a=1时,方程有三个实数解;0
例8.给定实数a,a≠0且a≠1,设函数y=(x∈R,x≠).
求证:这个函数图象关于直线y=x成轴对称图形。
【解析】(一)要证明f(x)的图象关于y=x对称,需要证明y=f(x)图象上任意一点P关于y=x的对称点P'仍在y=f(x)的图象上。因而设P(x0,y0)是y=f(x)上任一点,则y0=,而P(x0,y0)关于直线y=x的对称点的坐标为P'(y0,x0),只需验证P'(y0,x0)也在y=f(x)上。
∵ f(y0)===x0,
∴ (y0,x0)也在y=f(x)的图象上,
∴ y=f(x)=(x∈R,x≠)图象关于y=x对称。
(二)联想到函数与反函数图象之间的关系,我们只需证明函数的反函数就是它本身即可。从而由
y==()=(1+)
∵ x≠, ∴ ≠0, ∴y≠,
反解x,得x=( y≠) 即f-1(x)=(x≠),
∴ f(x)=f-1(x),又 ∵ y=f(x)与y=f-1(x)图象关于y=x对称,
∴ y=f(x)=(x≠)的图象关于直线y=x成轴对称图形。
【总结升华】函数与反函数的图象对称是两个函数关于y=x的对称问题,而本题是要证明函数图象自身关于y=x对称。
例9.若, , ,设为、、中的较大者,求的解析式。
【解析】在同一坐标系中做出三个函数、、的图象。
由图可知,的图象就是图中用红色标注的折线。
令,解出,即A点横坐标为,
令,解出, 即B点横坐标为
∴
【变式】当在实数集R上任取值时,函数相应的值等于、2 、三个之中最大的那个值.
(1)求与;
(2)在给定的坐标系中画出的图象,并写出的解析式;
【答案】
(1), .
(2)
【巩固练习】
1、给出下列四个对应:
① ② ③ ④
其构成映射的是 ( )
.只有①② .只有①④ .只有①③④ .只有③④
2、已知集合,,下列不表示从到的映射是( )
A. B.
C. D.
3、若函数的值域是,则函数的值域是( )
A. B. C. D.
4、设,则的定义域为( )
A. B.
C. D.
5、已知 ,,则( )
A.-4 B.4 C.-2 D.2
6、函数的图象是( )
A B C D
7、已知函数y=f(x)的图象关于直线x=-1对称,且当x>0时f(x)= ,则当x<-2时,f(x)=( )
A. - B. C. - D. -
8、汽车经过启动、加速行驶、匀速行驶、减速行驶之后停车,若把这一过程中汽车的行驶路程看作时间的函数,其图像可能是( )
A. B. C. D.
9、定义在上的函数满足(),,则等于( )
A.2 B.3 C.6 D.9
10、如果函数对任意都有,试求的值.
11、已知:集合,,映射满足,那么映射的个数是多少?
12、数的值域.
13、函数的值域
y=x2+4x+3 (-3≤x≤1)
14、公司拥有汽车100辆.当每辆车的月租金为3 000元时,可全部租出.当每辆车的月租金每增加50元时,未租出的车将会增加一辆.租出的车每月需要维护费150元,未租出的车每辆每月需要维护费50元.?
(1)当每辆车的月租金定为3 600元时,能租出多少辆车??
(2)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少??
15、知f(x)=x2+4x+3,求f(x)在区间[t,t+1]上的最小值g(t)和最大值h(t).
【答案与解析】
1、答案:
提示:根据映射的概念,集合到集合的映射是指对于集合中的每一个元素,在集合中都有唯一确定的值与之相对应,故选择.
2、答案:
提示:选项中,则对于集合中的元素4,对应的元素,不在集合中,不符合映射的概念.
3、答案:
解析:令,则,
4、答案:B
解析: 由得的定义域为
故,解得
故的定义域为。
5、答案:A
6、答案:A
7、答案:C
解析:由f(x)的图象关于直线x=-1对称得
f(x)=f(-2-x) ①
∴当x<-2时, -2-x>0
∴再由已知得 f(-2-x)= ②
于是由①②得当x<-2时 f(x)= ,
即f(x)= -,应选C.
8、答案:A.
解析:根据汽车加速行驶,匀速行驶,减速行驶结合函数图像可知。
9、答案:C
解析:∵ ( )
∴时,,即,
,时,,即,
,时,,即,
,时,,即.
10、解析:解:∵对任意,总有,
∴当时应有,
即.∴.
又∵,∴.
故有(,则.∴.
∴.
11、解析:满足,则只可能,即、、中可以全部为,或各取一个.
∵,且
∴有.
当时,只有一个映射;
当中恰有一个为,而另两个分别为,时,有个映射.因此所求的映射的个数为.
12、?解析:设,则,当时,y有最小值,所求函数的值域为.
13、解析:可借助数形结合思想利用它们的图象得到值域,即“图象法”.
画出y=x2+4x+3(-3≤x≤1)的图象,如图所示,
当x∈[-3,1]时,得y∈[-1,8]
14、解析:(1)当每辆车的月租金定为3 600元时,未租出的车辆数为=12,所以这时租出了88辆车.
(2)设每辆车的月租金定为x元,则租赁公司的月收益为f(x)=(100-×50.
整理得f(x)=- +162x-21 000=-(x-4 050)2+307 050.?
所以,当x=4 050时,f(x)最大,最大值为f(4 050)=307 050.
即当每辆车的月租金定为4 050元时,租赁公司的月收益最大,最大月收益为307 050元.
15、因抛物线的对称轴是x= -2,所以分类讨论:
(1) ①当t+1<-2,即t<-3时, g(t)=f(t+1);②当,即时g(t)=f(-2);③当t>-2时, g(t)=f(t).
(2) ①当 -2-t(t+1)-(-2), 即t时, h(t)= f(t); ②当-2-t< (t+1)-(-2), 即t时, h(t)= f(t+1).
综上所述:,
【学习目标】
了解构成函数的要素有定义域、对应法则、值域,会求一些简单函数的定义域和值域;掌握函数的三种表示方法(图象法、列表法、解析法),会根据不同的需要选择恰当的方法表示函数;了解简单的分段函数,并能简单应用,了解映射的概念,进一步了解函数式非空数集到非空数集的映射。
【要点梳理】
要点一、函数的概念
1.定义
设A、B是非空的数集,如果按照某个确定的对应关系f,使对于集合A中的任意一个数x,在集合B中都有唯一确定的数f(x)和它对应,那么就称f:A→B为从集合A到集合B的一个函数.
记作:y=f(x),xA.
其中,x叫做自变量,x的取值范围A叫做函数的定义域;与x的值相对应的y值叫做函数值,函数值的集合{f(x)|xA}叫做函数的值域.
要点诠释:
(1)A、B集合的非空性;(2)对应关系的存在性、唯一性、确定性;(3)A中元素的无剩余性;(4)B中元素的可剩余性。
2.区间的概念
(1)区间的分类:开区间、闭区间、半开半闭区间;
(2)无穷区间;
(3)区间的数轴表示.
区间表示:
{x|a≤x≤b}=[a,b];
; ;
.
要点二、映射
1.映射定义:
设A、B是两个非空集合,如果按照某个对应法则f,对于集合A中的任何一个元素,在集合B中都有唯一的元素和它对应,这样的对应叫做从A到B的映射;记为f:A→B.
象与原象:如果给定一个从集合A到集合B的映射,那么A中的元素a对应的B中的元素b叫做a的象,a叫做b的原象.
要点诠释:
(1)A中的每一个元素都有象,且唯一;
(2)B中的元素未必有原象,即使有,也未必唯一;
(3)a的象记为f(a).
2.函数与映射的区别与联系:
设A、B是两个非空数集,若f:A→B是从集合A到集合B的映射,这个映射叫做从集合A到集合B的函数,记为y=f(x).
要点诠释:
(1)函数一定是映射,映射不一定是函数;
(2)函数三要素:定义域、值域、对应法则;
(3)B中的元素未必有原象,即使有原象,也未必唯一;
(4)原象集合=定义域,值域=象集合.
要点三、函数的图象
函数的图象是函数关系的一种表示,它是从“形”的方面刻画函数的变化规律。通过函数图象,可以形象地反映函数的性质,利用函数图象既有助于记忆各类初等函数的性质,又可以运用数形结合的方法去解决某些问题。
在中学阶段,画函数图象有两种基本方法:
1、描点法,这种方法要与研究函数性质结合起来,切忌画图的随意性;
2、是图象变换法,它是把常见函数图象与图象变换的知识结合起来,可以研究各种不同函数的性质。在这一部分,首先应熟悉各种变换规则,并且从各个角度将不同变换方法进行对比,从中总结规律,达到熟练掌握的目的。
【典型例题】
类型一、映射的概念
例1.以下对应中,从集合A到集合B的映射有 ;其中 是函数 。
(1) (2) (3) (4)
【思路点拨】 依据映射的定义及函数的定义判断.
【解析】(1)、(2)、(4)是映射,(1)、(2)是函数。
【总结升华】
1.判断是否映射的方法:先看集合A中的每个元素是否在集合B中都有象;再看集合A中的每个元素的象是否唯一;
2.函数是非空数集到非空数集的特殊映射,函数一定是映射,映射不一定是函数.
举一反三:
【变式1】设集合A=R,集合B=R+,则从集合A到集合B的映射只可能是( )
A 、 B、
C、 D 、
【答案】C;
【解析】A、B、D中元素没有象。
【变式2】设集合,,则下述对应法则中,不能构成A到B的映射的是( )
A、 B、
C、 D、
【答案】D;
【解析】在D中在B中没有象。
例2. 已知在映射的作用下的像是,求在作用下的像和在 作用下的原像。
【思路点拨】求在作用下的像,即已知,求;求在 作用下的原像,即为已知,求.
【解析】,
所以在作用下的像是;
或
所以在作用下的原像是.
【总结升华】弄清题意,明白已知是什么,求的又是什么是本题的关键.
举一反三:
【变式】给定映射,点的原象是__________________。
【答案】;
【解析】
类型二、函数的概念
例3.下面各组函数中为相同函数的是( )
A、, B、,
C、, D、,
【思路点拨】判定两个函数相同的方法:当两个函数的三要素相同或者两个函数的对应法则与定义域相同时,两个函数是相同的。
【答案】C;
【解析】A中两函数的定义域不同,的定义域不含;B中两函数的定义域也不同,的定义域为,而的定义域为R;D中的对应法则不同。
【总结升华】对应法则相同与函数的解析式相同是不一样的,对应法则是函数的核心。
举一反三:
【变式】下列各组函数的图象相同的是( )
A、 B、
C、 D、
【答案】D;
【解析】实质为函数相同。A、C中两个函数的定义域不同;B中的对应法则不同。
例4.设,求,;
【思路点拨】 将看作一个整体,换元,求出,再求出.
【解析】设(),则(),
∴ ()
∴(),
().
【总结升华】换元法是常用的求解析式法,注意新元的范围,最后要给出函数的定义域;也可以用 配凑的方法;除以之外,若已知函数类型,还可以利用待定系数法求函数解析式。
举一反三:
【变式1】设,,则 .
【答案】;
【解析】.
类型三、函数的图象
例5.如下图可作为函数的图像的是( )
A B C D
【答案】D;
【解析】作为函数的图像,就看每一个自变量是否对应唯一一个函数值。
例6.把函数y=(x-2)2+2的图象向左平移一个单位,再向上平移一个单位,所得图象对应的函数解析式为_________。
【思路点拨】关于函数图象变换经常会考察这两个内容,给出函数解析式说明变换过程,或给出变换过程写解析式。
【解析】把图象左移一个单位,解析式变为y=(x+1-2)2+2=(x-1)2+2,向上平移一个单位,解析式变为y=[(x-1)2+2]+1=(x-1)2+3.
例7.试讨论方程 |x2-4x+3|=a的解的个数(a∈R).
【解析】本题采用数形结合的方式。
把方程的解的个数看成函数y=|x2-4x+3|和函数y=a的交点个数。
y=|x2-4x+3|的图象是y'=x2-4x+3的图象保留x轴以上部分,将x轴以下部分沿x轴翻折上来形成的图象,而y=a是一条垂直于y轴的直线,如图,由图象可知,a<0时,方程无实解。a=0或a>1时,方程有两个实数解;a=1时,方程有三个实数解;0
例8.给定实数a,a≠0且a≠1,设函数y=(x∈R,x≠).
求证:这个函数图象关于直线y=x成轴对称图形。
【解析】(一)要证明f(x)的图象关于y=x对称,需要证明y=f(x)图象上任意一点P关于y=x的对称点P'仍在y=f(x)的图象上。因而设P(x0,y0)是y=f(x)上任一点,则y0=,而P(x0,y0)关于直线y=x的对称点的坐标为P'(y0,x0),只需验证P'(y0,x0)也在y=f(x)上。
∵ f(y0)===x0,
∴ (y0,x0)也在y=f(x)的图象上,
∴ y=f(x)=(x∈R,x≠)图象关于y=x对称。
(二)联想到函数与反函数图象之间的关系,我们只需证明函数的反函数就是它本身即可。从而由
y==()=(1+)
∵ x≠, ∴ ≠0, ∴y≠,
反解x,得x=( y≠) 即f-1(x)=(x≠),
∴ f(x)=f-1(x),又 ∵ y=f(x)与y=f-1(x)图象关于y=x对称,
∴ y=f(x)=(x≠)的图象关于直线y=x成轴对称图形。
【总结升华】函数与反函数的图象对称是两个函数关于y=x的对称问题,而本题是要证明函数图象自身关于y=x对称。
例9.若, , ,设为、、中的较大者,求的解析式。
【解析】在同一坐标系中做出三个函数、、的图象。
由图可知,的图象就是图中用红色标注的折线。
令,解出,即A点横坐标为,
令,解出, 即B点横坐标为
∴
【变式】当在实数集R上任取值时,函数相应的值等于、2 、三个之中最大的那个值.
(1)求与;
(2)在给定的坐标系中画出的图象,并写出的解析式;
【答案】
(1), .
(2)
【巩固练习】
1、给出下列四个对应:
① ② ③ ④
其构成映射的是 ( )
.只有①② .只有①④ .只有①③④ .只有③④
2、已知集合,,下列不表示从到的映射是( )
A. B.
C. D.
3、若函数的值域是,则函数的值域是( )
A. B. C. D.
4、设,则的定义域为( )
A. B.
C. D.
5、已知 ,,则( )
A.-4 B.4 C.-2 D.2
6、函数的图象是( )
A B C D
7、已知函数y=f(x)的图象关于直线x=-1对称,且当x>0时f(x)= ,则当x<-2时,f(x)=( )
A. - B. C. - D. -
8、汽车经过启动、加速行驶、匀速行驶、减速行驶之后停车,若把这一过程中汽车的行驶路程看作时间的函数,其图像可能是( )
A. B. C. D.
9、定义在上的函数满足(),,则等于( )
A.2 B.3 C.6 D.9
10、如果函数对任意都有,试求的值.
11、已知:集合,,映射满足,那么映射的个数是多少?
12、数的值域.
13、函数的值域
y=x2+4x+3 (-3≤x≤1)
14、公司拥有汽车100辆.当每辆车的月租金为3 000元时,可全部租出.当每辆车的月租金每增加50元时,未租出的车将会增加一辆.租出的车每月需要维护费150元,未租出的车每辆每月需要维护费50元.?
(1)当每辆车的月租金定为3 600元时,能租出多少辆车??
(2)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少??
15、知f(x)=x2+4x+3,求f(x)在区间[t,t+1]上的最小值g(t)和最大值h(t).
【答案与解析】
1、答案:
提示:根据映射的概念,集合到集合的映射是指对于集合中的每一个元素,在集合中都有唯一确定的值与之相对应,故选择.
2、答案:
提示:选项中,则对于集合中的元素4,对应的元素,不在集合中,不符合映射的概念.
3、答案:
解析:令,则,
4、答案:B
解析: 由得的定义域为
故,解得
故的定义域为。
5、答案:A
6、答案:A
7、答案:C
解析:由f(x)的图象关于直线x=-1对称得
f(x)=f(-2-x) ①
∴当x<-2时, -2-x>0
∴再由已知得 f(-2-x)= ②
于是由①②得当x<-2时 f(x)= ,
即f(x)= -,应选C.
8、答案:A.
解析:根据汽车加速行驶,匀速行驶,减速行驶结合函数图像可知。
9、答案:C
解析:∵ ( )
∴时,,即,
,时,,即,
,时,,即,
,时,,即.
10、解析:解:∵对任意,总有,
∴当时应有,
即.∴.
又∵,∴.
故有(,则.∴.
∴.
11、解析:满足,则只可能,即、、中可以全部为,或各取一个.
∵,且
∴有.
当时,只有一个映射;
当中恰有一个为,而另两个分别为,时,有个映射.因此所求的映射的个数为.
12、?解析:设,则,当时,y有最小值,所求函数的值域为.
13、解析:可借助数形结合思想利用它们的图象得到值域,即“图象法”.
画出y=x2+4x+3(-3≤x≤1)的图象,如图所示,
当x∈[-3,1]时,得y∈[-1,8]
14、解析:(1)当每辆车的月租金定为3 600元时,未租出的车辆数为=12,所以这时租出了88辆车.
(2)设每辆车的月租金定为x元,则租赁公司的月收益为f(x)=(100-×50.
整理得f(x)=- +162x-21 000=-(x-4 050)2+307 050.?
所以,当x=4 050时,f(x)最大,最大值为f(4 050)=307 050.
即当每辆车的月租金定为4 050元时,租赁公司的月收益最大,最大月收益为307 050元.
15、因抛物线的对称轴是x= -2,所以分类讨论:
(1) ①当t+1<-2,即t<-3时, g(t)=f(t+1);②当,即时g(t)=f(-2);③当t>-2时, g(t)=f(t).
(2) ①当 -2-t(t+1)-(-2), 即t时, h(t)= f(t); ②当-2-t< (t+1)-(-2), 即t时, h(t)= f(t+1).
综上所述:,
