青岛版七年级下册9.2 平行线和它的画法 教学设计
文档属性
| 名称 | 青岛版七年级下册9.2 平行线和它的画法 教学设计 |

|
|
| 格式 | zip | ||
| 文件大小 | 103.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-29 18:43:28 | ||
图片预览


文档简介
9.2 平行线和它的画法
【教学目标】
1.理解平面内两条直线平行的概念和表示方法.
2.会利用三角尺和直尺过已知直线外一点画这条直线的平行线.
3.理解并掌握平行线的基本性质.
【教学重难点】
重点:会利用一副三角尺过一点画已知直线的平行线.
难点:掌握”经过直线外一点能且只能画一条直线与书籍直线平行”的结论.
【评价设计】
1、经历探索完全平方公式的过程,发展学生符号意识和推理能力。在探索讨论归纳总结中培养学生有条理的语言表达能力和逻辑思维能力.经历发现、推导公式的过程,培养学生发现问题、解决问题的能力,发展实践能力.
2、通过学生积极参与探索活动,培养主动探究、合作交流的学习习惯。鼓励学生大胆尝试发表自己的见解,培养学生敢于面对挑战的意志,并获得成功的体验激发学习热情和兴趣增强学习数学的信心.
【教学活动设计】
教学环节 教与学活动 评价任务
导入环节 (2分钟) 平行线是我们日常生活中经常见到的图形, 你能举一些生活中平行线的实例吗?
先学环节 (13分钟) 自主探究要求:1.阅读课本P28的图片,解释平行线的定义和表示方法。 (一)平行线定义及表示方法 (1)在同一平面内, 的两条直线叫平行线。 (2)如图,直线AB与直线CD平行,记作 ,读作 。 2.阅读教材P29实验与探究。 (1)按要求画图 请你用一副三角板画出已知直线的平行线 . P 总结: 平行线画法:一放、二靠、三推、四画. (2)过直线AB外一点P画直线AB的平行线, 通过画图你发现过一点能画多少条直线与已知直线平行? 你发现的结论为 。(二)平行公理及推论思考:下图中,①过点B画直线a的平行线,能画 条; ②过点C画直线a的平行线,能画 条; ③你画的直线有什么位置关系? 平行公理 公理内容: 。推论: 。 学生经自己的研究成果记录下来。
后教环节 (15分钟) 合作探究先独立思考,然后小组内交流,小组长掌握好节奏和发言的顺序,完成下面问题。如果直线b//a,c//a,那么直线b与直线c能否相交于点M,你能结合平行线的性质解释一下吗? 学生先独立思考,再小组合作探究,然后再展示与点评。
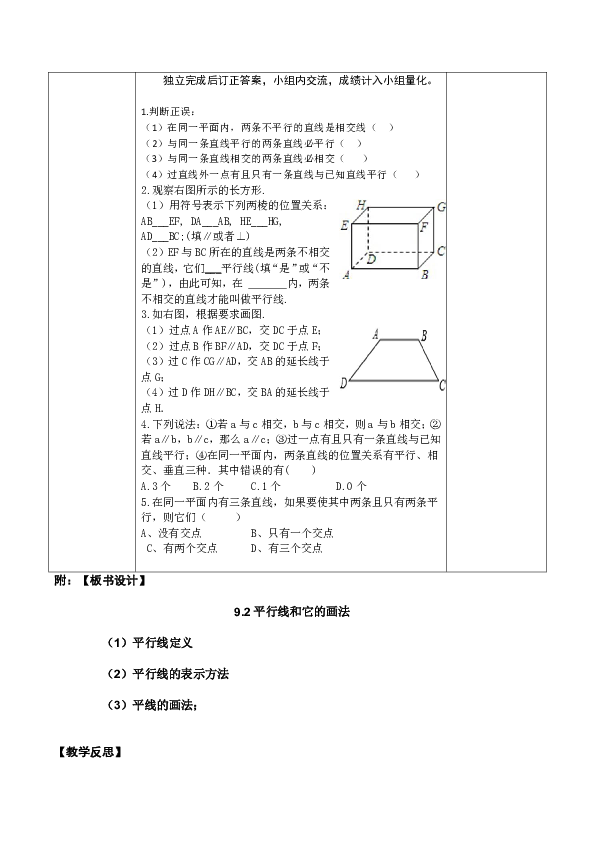
训练环节 (10分钟) 课堂小测1、填空(1)在同一平面内, 的两条直线叫平行线。 (2)如图,直线AB与直线CD平行,记作 ,读作 。 (3)经过 ,能且只能画一条直线与已知直线平行。 当堂训练独立完成后订正答案,小组内交流,成绩计入小组量化。1.判断正误:(1)在同一平面内,两条不平行的直线是相交线( )(2)与同一条直线平行的两条直线必平行( )(3)与同一条直线相交的两条直线必相交( )(4)过直线外一点有且只有一条直线与已知直线平行( )2.观察右图所示的长方形.(1)用符号表示下列两棱的位置关系:AB___EF, DA___AB, HE___HG, AD___BC;(填∥或者⊥)(2)EF与BC所在的直线是两条不相交的直线,它们___平行线(填“是”或“不是”),由此可知,在 内,两条不相交的直线才能叫做平行线.3.如右图,根据要求画图.(1)过点A作AE∥BC,交DC于点E;(2)过点B作BF∥AD,交DC于点F;(3)过C作CG∥AD,交AB的延长线于点G;(4)过D作DH∥BC,交BA的延长线于点H. 4.下列说法:①若a与c相交,b与c相交,则a与b相交;②若a∥b,b∥c,那么a∥c;③过一点有且只有一条直线与已知直线平行;④在同一平面内,两条直线的位置关系有平行、相交、垂直三种.其中错误的有( ) A.3个 B.2个 C.1个 D.0个5.在同一平面内有三条直线,如果要使其中两条且只有两条平行,则它们( ) A、没有交点 B、只有一个交点 C、有两个交点 D、有三个交点 学生独立完成,根据学生的完成情况,小组内交换,互相批阅,根据对题情况按每全对1人记2分计入小组量化。
附:【板书设计】
9.2平行线和它的画法
(1)平行线定义
(2)平行线的表示方法
(3)平线的画法;
【教学反思】
D
A
C
B
【教学目标】
1.理解平面内两条直线平行的概念和表示方法.
2.会利用三角尺和直尺过已知直线外一点画这条直线的平行线.
3.理解并掌握平行线的基本性质.
【教学重难点】
重点:会利用一副三角尺过一点画已知直线的平行线.
难点:掌握”经过直线外一点能且只能画一条直线与书籍直线平行”的结论.
【评价设计】
1、经历探索完全平方公式的过程,发展学生符号意识和推理能力。在探索讨论归纳总结中培养学生有条理的语言表达能力和逻辑思维能力.经历发现、推导公式的过程,培养学生发现问题、解决问题的能力,发展实践能力.
2、通过学生积极参与探索活动,培养主动探究、合作交流的学习习惯。鼓励学生大胆尝试发表自己的见解,培养学生敢于面对挑战的意志,并获得成功的体验激发学习热情和兴趣增强学习数学的信心.
【教学活动设计】
教学环节 教与学活动 评价任务
导入环节 (2分钟) 平行线是我们日常生活中经常见到的图形, 你能举一些生活中平行线的实例吗?
先学环节 (13分钟) 自主探究要求:1.阅读课本P28的图片,解释平行线的定义和表示方法。 (一)平行线定义及表示方法 (1)在同一平面内, 的两条直线叫平行线。 (2)如图,直线AB与直线CD平行,记作 ,读作 。 2.阅读教材P29实验与探究。 (1)按要求画图 请你用一副三角板画出已知直线的平行线 . P 总结: 平行线画法:一放、二靠、三推、四画. (2)过直线AB外一点P画直线AB的平行线, 通过画图你发现过一点能画多少条直线与已知直线平行? 你发现的结论为 。(二)平行公理及推论思考:下图中,①过点B画直线a的平行线,能画 条; ②过点C画直线a的平行线,能画 条; ③你画的直线有什么位置关系? 平行公理 公理内容: 。推论: 。 学生经自己的研究成果记录下来。
后教环节 (15分钟) 合作探究先独立思考,然后小组内交流,小组长掌握好节奏和发言的顺序,完成下面问题。如果直线b//a,c//a,那么直线b与直线c能否相交于点M,你能结合平行线的性质解释一下吗? 学生先独立思考,再小组合作探究,然后再展示与点评。
训练环节 (10分钟) 课堂小测1、填空(1)在同一平面内, 的两条直线叫平行线。 (2)如图,直线AB与直线CD平行,记作 ,读作 。 (3)经过 ,能且只能画一条直线与已知直线平行。 当堂训练独立完成后订正答案,小组内交流,成绩计入小组量化。1.判断正误:(1)在同一平面内,两条不平行的直线是相交线( )(2)与同一条直线平行的两条直线必平行( )(3)与同一条直线相交的两条直线必相交( )(4)过直线外一点有且只有一条直线与已知直线平行( )2.观察右图所示的长方形.(1)用符号表示下列两棱的位置关系:AB___EF, DA___AB, HE___HG, AD___BC;(填∥或者⊥)(2)EF与BC所在的直线是两条不相交的直线,它们___平行线(填“是”或“不是”),由此可知,在 内,两条不相交的直线才能叫做平行线.3.如右图,根据要求画图.(1)过点A作AE∥BC,交DC于点E;(2)过点B作BF∥AD,交DC于点F;(3)过C作CG∥AD,交AB的延长线于点G;(4)过D作DH∥BC,交BA的延长线于点H. 4.下列说法:①若a与c相交,b与c相交,则a与b相交;②若a∥b,b∥c,那么a∥c;③过一点有且只有一条直线与已知直线平行;④在同一平面内,两条直线的位置关系有平行、相交、垂直三种.其中错误的有( ) A.3个 B.2个 C.1个 D.0个5.在同一平面内有三条直线,如果要使其中两条且只有两条平行,则它们( ) A、没有交点 B、只有一个交点 C、有两个交点 D、有三个交点 学生独立完成,根据学生的完成情况,小组内交换,互相批阅,根据对题情况按每全对1人记2分计入小组量化。
附:【板书设计】
9.2平行线和它的画法
(1)平行线定义
(2)平行线的表示方法
(3)平线的画法;
【教学反思】
D
A
C
B
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
