人教版八年级数学上册第十二章全等三角形秒解教案
文档属性
| 名称 | 人教版八年级数学上册第十二章全等三角形秒解教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 348.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-01 00:00:00 | ||
图片预览


文档简介
秒解全等三角形
回顾知识点:
判定三角形全等的方法
SSS: 三条边对应相等的两个三角形全等;
SAS: 两条边对应相等,且夹角也相等的两个三角形全等;
ASA:两角对应相等,且夹边也相等的两个三角形全等;
AAS:两角对应相等,且其中一角的对边也相等的两个三角形全等;
HL:一条直角边和斜边分别对应相等的两个直角三角形全等。(直
角三角形)
寻找全等三角形常用的方法:
一:题目中出现的问题或者结论
线段相等
角相等
度数
线段或者线段的和、差、倍、分关系
然后根据题目中出现的三角形,进行猜测验证,寻找两个三角形
相关的边以及角之间的关系,利用相关的判定定理进行证明即可。
二、已知条件入手
审题的时候,对题目中出现的图形已知条件进行标注,注意不同
的区分,如果理想思维不强,可以利用不同颜色的笔进行标注。然后
根据标注的条件对比判定定理,进行未知条件的推理。
经典题型:
题目中出现角平分线
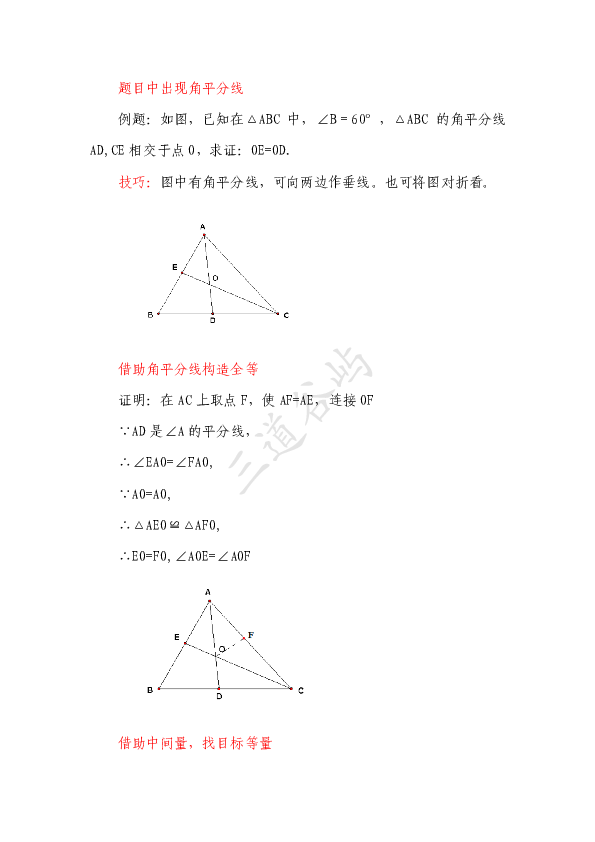
例题:如图,已知在△ABC 中,∠B=60°,△ABC 的角平分线
AD,CE 相交于点 O,求证:OE=OD.
技巧:图中有角平分线,可向两边作垂线。也可将图对折看。
借助角平分线构造全等
证明:在 AC 上取点 F,使 AF=AE,连接 OF
∵AD 是∠A 的平分线,
∴∠EAO=∠FAO,
∵AO=AO,
∴△AEO≌△AFO,
∴EO=FO,∠AOE=∠AOF
借助中间量,找目标等量
∵CE 是∠C 的角平分线,
∴∠DCO=∠FCO,
∵∠B=60°
∴∠BAC+∠ACB=120°
∴∠COD=∠CAO+∠OCA=
1
2
(∠BAC+∠ACB)=60°
∵∠AOE=∠AOF,∠AOE=∠COD 即∠AOF=∠COD=60°
∴∠COF=180°-∠COD-∠AOF=60°
∴∠COF=∠COD
根据全等性质转化得到答案
∵OC=OC
∴△OCD≌△OCF
∴OD=OF
∴OE=OD
题目中出现中点或中线(中位线)
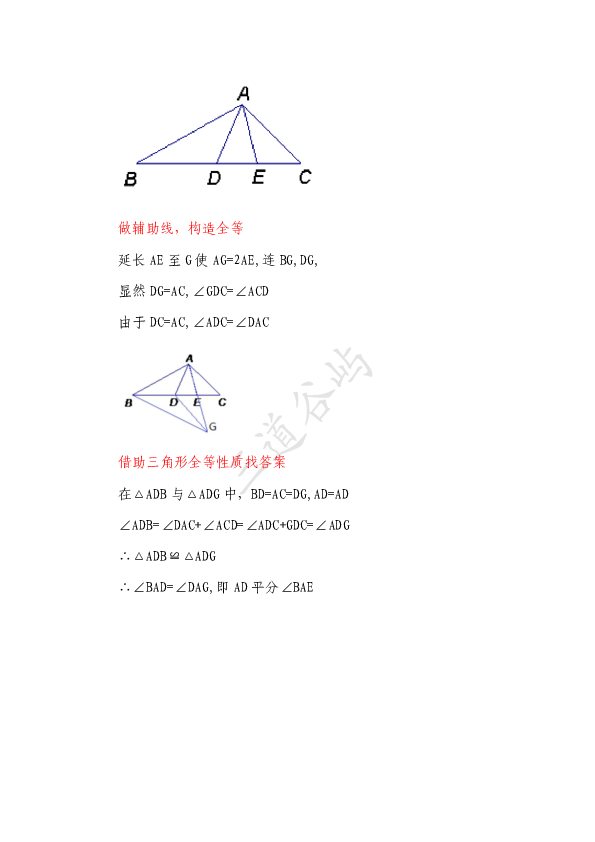
例题:如图,△ABC 中,BD=DC=AC,E 是 DC的中点,求证 AD平分
∠BAE.
技巧:图中有中点或中线,中线延长二倍位置得全等。
做辅助线,构造全等
延长 AE 至 G使 AG=2AE,连 BG,DG,
显然 DG=AC,∠GDC=∠ACD
由于 DC=AC,∠ADC=∠DAC
借助三角形全等性质找答案
在△ADB 与△ADG 中,BD=AC=DG,AD=AD
∠ADB=∠DAC+∠ACD=∠ADC+GDC=∠ADG
∴△ADB≌△ADG
∴∠BAD=∠DAG,即 AD 平分∠BAE
练习:
1、如图,AC∥BD,E 为 CD 的中点,AE⊥BE, AE⊥BE.
求证:AE 平分∠BAC.
如图所示,延长 AE交 BD 的延长线于 F,
∵AC∥BD,
∴∠CAE=∠DFE,
∵E 为 CD 的中点,
∴CE=DE,在△CAE 和△DFE 中,
∠CAE=∠DFE
∠AEC=∠FED
CE=DE
∴△CAE≌△DFE(AAS)
∴AC=DF,AE=FE
∵AE⊥BE,
∴∠AEB=∠FEB=90°,
在△AEB 和△FEB 中
AE=FE,
∠AEB=∠FEB,
BE=BE
∴△AEB≌△FEB(SAS)
∴∠BAE=∠F
∴∠CAE=∠BAE
∴AE 平分∠BAC
2、如图,在△ABC 中,AD 平分∠BAC.
求证:????????????????????: ????????????????????=AB:AC
证明:过 D 作 DE⊥AB 于 E,DF⊥AC 于 F,
∵AD 平分∠BAC,
∴DE=DF,
∵????????????????????=
1
2
AB.DE, ????????????????????=
1
2
AC.DF
∴????????????????????: ????????????????????= AB:AC
3、如图,已知在△ABC 中, D 为 AC 中点,连接 BD.若
AB=10cm,BC=6cm,求中线 BD的取值范围。
解:如图,延长 BD至 E,使 BD=DE,连接 CE,
∵D 为 AC 中点
∴AD=DC,
在△ABD 和△CED 中,
BD=DE,
∠ADB=∠CDE
AD=CD
∴△ABD≌△CED(SAS)
∴EC=AB=10
在△BCE 中,CE-BC<BE<CE+BC
10-6<BE<10+6
∴4<2BD<16
∴2<BD<8
4、如图,AC 平分∠BAD,CD=CB,AB>AD,求证:∠B+∠ADC=180°
作 CF⊥AB 于点 F,CE⊥AD交 AD 延长线于点 E,
∵AC 平分∠BAD,∴CE=CF
在 Rt△CDE 与 Rt△CBF 中,
CF=CE
BC=CD
∴Rt△CDE≌Rt△CBF(HL)
∴∠B=∠CDE
∴∠B+∠ADC=180°
