陕西省2020年中考数学圆的分类综合训练(无答案)
文档属性
| 名称 | 陕西省2020年中考数学圆的分类综合训练(无答案) | 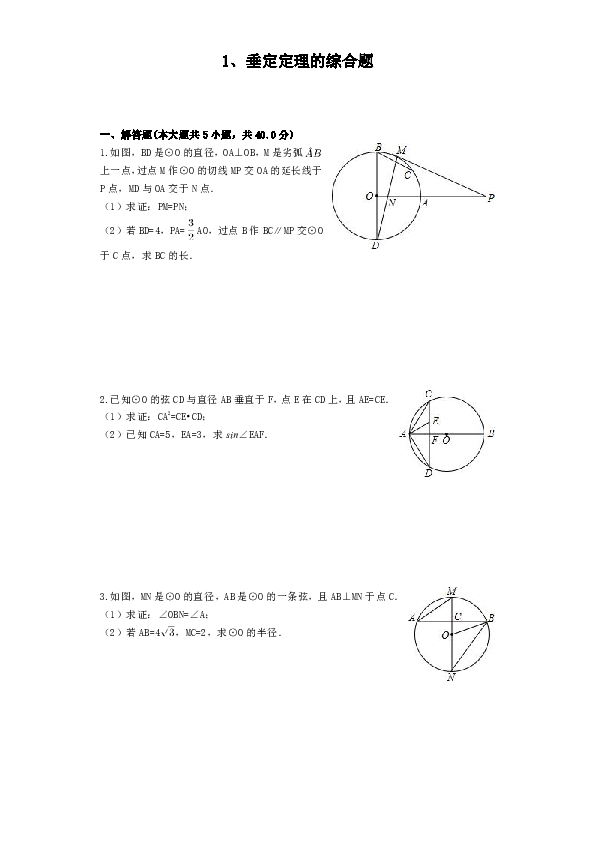 | |
| 格式 | zip | ||
| 文件大小 | 173.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-29 13:39:08 | ||
图片预览



文档简介
1、垂定定理的综合题
一、解答题(本大题共5小题,共40.0分)
1.如图,BD是⊙O的直径,OA⊥OB,M是劣弧上一点,过点M作⊙O的切线MP交OA的延长线于P点,MD与OA交于N点.
(1)求证:PM=PN;
(2)若BD=4,PA=AO,过点B作BC∥MP交⊙O于C点,求BC的长.
2.已知⊙O的弦CD与直径AB垂直于F,点E在CD上,且AE=CE.
(1)求证:CA2=CE?CD;
(2)已知CA=5,EA=3,求sin∠EAF.
3.如图,MN是⊙O的直径,AB是⊙O的一条弦,且AB⊥MN于点C.
(1)求证:∠OBN=∠A;
(2)若AB=4,MC=2,求⊙O的半径.
4.如图,AB是⊙O的直径,CD与⊙O相切于点C,DA⊥AB,DO及DO的延长线与⊙O分别相交于点E、F,EB与CF相交于点G.
(1)求证:DA=DC;
(2)⊙O的半径为3,DC=4,求CG的长.
5.已知:如图,AB为⊙O的直径,C、D是半圆弧上的两点,E是AB上除O外的一点,AC与DE相交于F.①,②DE⊥AB,③AF=DF.
(1)写出“以①②③中的任意两个为条件,推出第三个(结论)”的一个正确命题,并加以证明;
(2)“以①②③中的任意两个为条件,推出笫三个(结论)”可以组成多少个正确的命题?(不必说明理由)
2、圆周角的推论综合题
一、解答题(本大题共3小题,共24.0分)
1.如图所示,△ABC内接于⊙O,AB是⊙O的直径,点D在⊙O上,过点C的切线交AD的延长线于点E,且AE⊥CE,连接CD.
(1)求证:DC=BC;
(2)若AB=5,AC=4,求tan∠DCE的值.
2.如图,BC为⊙O的直径,AD⊥BC于D,P是上一动点,连接PB分别交AD、AC于点E,F.
(1)当=时,求证:AE=BE;
(2)当点P在什么位置时,AF=EF?证明你的结论.
3.如图,MN是⊙O的直径,AB是⊙O的一条弦,且AB⊥MN于点C.
(1)求证:∠OBN=∠A;
(2)若AB=4,MC=2,求⊙O的半径.
3、切线判定的综合题
一、解答题(本大题共6小题,共48.0分)
1.如图,已知⊙O的半径为1,AC是⊙O的直径,过点C作⊙O的切线BC,E是BC的中点,AB交⊙O于D点.
(1)直接写出ED和EC的数量关系: ______ ;
(2)DE是⊙O的切线吗?若是,给出证明;若不是,说明理由;
(3)填空:当BC= ______ 时,四边形AOED是平行四边形,同时以点O、D、E、C为顶点的四边形是 ______ .
2.已知:如图,AB是⊙O的直径,AB=6,延长AB到点C,使BC=AB,D是⊙O上一点,DC=.求证:
(1)△CDB∽△CAD;
(2)CD是⊙O的切线.
3.如图,AB、AC分别是⊙O的直径和弦,点D为劣弧AC上一点,弦DE⊥AB分别交⊙O于E,交AB于H,交AC于F.P是ED延长线上一点且PC=PF.
(1)求证:PC是⊙O的切线;
(2)点D在劣弧AC什么位置时,才能使AD2=DE?DF,为什么?
(3)在(2)的条件下,若OH=1,AH=2,求弦AC的长.
4.如图,AB是⊙O的直径,点C在⊙O上,∠CAB的平分线交⊙O于点D,过点D作AC的垂线交AC的延长线于点E,连接BC交AD于点F.
(1)猜想ED与⊙O的位置关系,并证明你的猜想;
(2)若AB=6,AD=5,求AF的长.
5.如图,在△ABC中,∠C=90°,∠BAC的平分线AD交BC于D,过点D作DE⊥AD交AB于E,以AE为直径作⊙O.
(1)求证:点D在⊙O上;
(2)求证:BC是⊙O的切线;
(3)若AC=6,BC=8,求△BDE的面积.
6.如图,AB是⊙O的直径,CD与⊙O相切于点C,DA⊥AB,DO及DO的延长线与⊙O分别相交于点E、F,EB与CF相交于点G.
(1)求证:DA=DC;
(2)⊙O的半径为3,DC=4,求CG的长.
4、圆与圆的位置关系的综合题
一、解答题(本大题共3小题,共24.0分)
1.已知点P在线段AB上,点O在线段AB延长线上.以点O为圆心,OP为半径作圆,点C是圆O上的一点.
(1)如图,如果AP=2PB,PB=BO.求证:△CAO∽△BCO;
(2)如果AP=m(m是常数,且m>1),BP=1,OP是OA,OB的比例中项.当点C在圆O上运动时,求AC:BC的值(结果用含m的式子表示);
(3)在(2)的条件下,讨论以BC为半径的圆B和以CA为半径的圆C的位置关系,并写出相应m的取值范围.
2.如图,BD是⊙O的直径,OA⊥OB,M是劣弧上一点,过点M作⊙O的切线MP交OA的延长线于P点,MD与OA交于N点.
(1)求证:PM=PN;
(2)若BD=4,PA=AO,过点B作BC∥MP交⊙O于C点,求BC的长.
3、如图,在平面直角坐标系中,以坐标原点O为圆心,2为半径画⊙O,P是⊙O上一动点,且P在第一象限内,过点P作⊙O的切线与x轴相交于点A,与y轴相交于点B.
(1)点P在运动时,线段AB的长度也在发生变化,请写出线段AB长度的最小值,并说明理由;
(2)在⊙O上是否存在一点Q,使得以Q,O,A,P为顶点的四边形是平行四边形?若存在,请求出Q点的坐标;若不存在,请说明理由.
5、圆的内接四边形综合题
一、解答题(本大题共4小题,共32.0分)
1.如图,在Rt△ABC中,斜边BC=12,∠C=30°,D为BC的中点,△ABD的外接圆⊙O与AC交于F点,过A作⊙O的切线AE交DF的延长线于E点.
(1)求证:AE⊥DE;
(2)计算:AC?AF的值.
2.如图,⊙O为△ABC的外接圆,且AB=AC,过点A的直线交⊙O于D,交BC延长线于F,DE是BD的延长线,连接CD.
(1)求证:∠EDF=∠CDF;
(2)求证:AB2=AF?AD;
(3)若BD是⊙O的直径,且∠EDC=120°,BC=6cm,求AF的长.
如图,⊙C经过坐标原点,且与两坐标轴分别交于点A与点B,点A的坐标为(0,4),M是圆上一点,∠BMO=120°.
(1)求证:AB为⊙C直径;
(2)求⊙C的半径及圆心C的坐标.
4.如图所示,圆O是△ABC的外接圆,∠BAC与∠ABC的平分线相交于点I,延长AI交圆O于点D,连接BD、DC.
(1)求证:BD=DC=DI;
(2)若圆O的半径为10cm,∠BAC=120°,求△BDC的面积.
6、圆的其他的综合题
一、解答题(本大题共5小题,共40.0分)
1.如图,⊙O的半径为,⊙O的内接一个正多边形,边心距为1,求它的中心角、边长、面积.
2.如图,在扇形OAB中,∠AOB=90°,半径OA=6.将扇形OAB沿过点B的直线折叠,点O恰好落在上点D处,折痕交OA于点C,求整个阴影部分的周长和面积.
3.如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠D=30°.
(1)判断直线CD和⊙O的位置关系,并说明理由;
(2)若⊙O的半径为3,求的长.(结果保留π)
4.如图,已知△ABC,AC=BC=6,∠C=90度.O是AB的中点,⊙O与AC相切于点D、与BC相切于点E.设⊙O交OB于F,连DF并延长交CB的延长线于G.
(1)∠BFG与∠BGF是否相等?为什么?
(2)求由DG、GE和弧ED所围成图形的面积.(阴影部分)
5.如图,在△ABC中,∠ABC=90°,D是边AC上的一点,连接BD,使∠A=2∠1,E是BC上的一点,以BE为直径的⊙O经过点D.
(1)求证:AC是⊙O的切线;
(2)若∠A=60°,⊙O的半径为2,求阴影部分的面积.(结果保留根号和π)
6、如图,在Rt△ABC中,斜边BC=12,∠C=30°,D为BC的中点,△ABD的外接圆⊙O与AC交于F点,过A作⊙O的切线AE交DF的延长线于E点.
(1)求证:AE⊥DE;
(2)计算:AC?AF的值.
7、如图,⊙O为△ABC的外接圆,且AB=AC,过点A的直线交⊙O于D,交BC延长线于F,DE是BD的延长线,连接CD.
(1)求证:∠EDF=∠CDF;
(2)求证:AB2=AF?AD;
(3)若BD是⊙O的直径,且∠EDC=120°,BC=6cm,求AF的长.
8.如图,⊙C经过坐标原点,且与两坐标轴分别交于点A与点B,点A的坐标为(0,4),M是圆上一点,∠BMO=120°.
(1)求证:AB为⊙C直径;
(2)求⊙C的半径及圆心C的坐标.
9.如图所示,圆O是△ABC的外接圆,∠BAC与∠ABC的平分线相交于点I,延长AI交圆O于点D,连接BD、DC.
(1)求证:BD=DC=DI;
(2)若圆O的半径为10cm,∠BAC=120°,求△BDC的面积.
一、解答题(本大题共5小题,共40.0分)
1.如图,BD是⊙O的直径,OA⊥OB,M是劣弧上一点,过点M作⊙O的切线MP交OA的延长线于P点,MD与OA交于N点.
(1)求证:PM=PN;
(2)若BD=4,PA=AO,过点B作BC∥MP交⊙O于C点,求BC的长.
2.已知⊙O的弦CD与直径AB垂直于F,点E在CD上,且AE=CE.
(1)求证:CA2=CE?CD;
(2)已知CA=5,EA=3,求sin∠EAF.
3.如图,MN是⊙O的直径,AB是⊙O的一条弦,且AB⊥MN于点C.
(1)求证:∠OBN=∠A;
(2)若AB=4,MC=2,求⊙O的半径.
4.如图,AB是⊙O的直径,CD与⊙O相切于点C,DA⊥AB,DO及DO的延长线与⊙O分别相交于点E、F,EB与CF相交于点G.
(1)求证:DA=DC;
(2)⊙O的半径为3,DC=4,求CG的长.
5.已知:如图,AB为⊙O的直径,C、D是半圆弧上的两点,E是AB上除O外的一点,AC与DE相交于F.①,②DE⊥AB,③AF=DF.
(1)写出“以①②③中的任意两个为条件,推出第三个(结论)”的一个正确命题,并加以证明;
(2)“以①②③中的任意两个为条件,推出笫三个(结论)”可以组成多少个正确的命题?(不必说明理由)
2、圆周角的推论综合题
一、解答题(本大题共3小题,共24.0分)
1.如图所示,△ABC内接于⊙O,AB是⊙O的直径,点D在⊙O上,过点C的切线交AD的延长线于点E,且AE⊥CE,连接CD.
(1)求证:DC=BC;
(2)若AB=5,AC=4,求tan∠DCE的值.
2.如图,BC为⊙O的直径,AD⊥BC于D,P是上一动点,连接PB分别交AD、AC于点E,F.
(1)当=时,求证:AE=BE;
(2)当点P在什么位置时,AF=EF?证明你的结论.
3.如图,MN是⊙O的直径,AB是⊙O的一条弦,且AB⊥MN于点C.
(1)求证:∠OBN=∠A;
(2)若AB=4,MC=2,求⊙O的半径.
3、切线判定的综合题
一、解答题(本大题共6小题,共48.0分)
1.如图,已知⊙O的半径为1,AC是⊙O的直径,过点C作⊙O的切线BC,E是BC的中点,AB交⊙O于D点.
(1)直接写出ED和EC的数量关系: ______ ;
(2)DE是⊙O的切线吗?若是,给出证明;若不是,说明理由;
(3)填空:当BC= ______ 时,四边形AOED是平行四边形,同时以点O、D、E、C为顶点的四边形是 ______ .
2.已知:如图,AB是⊙O的直径,AB=6,延长AB到点C,使BC=AB,D是⊙O上一点,DC=.求证:
(1)△CDB∽△CAD;
(2)CD是⊙O的切线.
3.如图,AB、AC分别是⊙O的直径和弦,点D为劣弧AC上一点,弦DE⊥AB分别交⊙O于E,交AB于H,交AC于F.P是ED延长线上一点且PC=PF.
(1)求证:PC是⊙O的切线;
(2)点D在劣弧AC什么位置时,才能使AD2=DE?DF,为什么?
(3)在(2)的条件下,若OH=1,AH=2,求弦AC的长.
4.如图,AB是⊙O的直径,点C在⊙O上,∠CAB的平分线交⊙O于点D,过点D作AC的垂线交AC的延长线于点E,连接BC交AD于点F.
(1)猜想ED与⊙O的位置关系,并证明你的猜想;
(2)若AB=6,AD=5,求AF的长.
5.如图,在△ABC中,∠C=90°,∠BAC的平分线AD交BC于D,过点D作DE⊥AD交AB于E,以AE为直径作⊙O.
(1)求证:点D在⊙O上;
(2)求证:BC是⊙O的切线;
(3)若AC=6,BC=8,求△BDE的面积.
6.如图,AB是⊙O的直径,CD与⊙O相切于点C,DA⊥AB,DO及DO的延长线与⊙O分别相交于点E、F,EB与CF相交于点G.
(1)求证:DA=DC;
(2)⊙O的半径为3,DC=4,求CG的长.
4、圆与圆的位置关系的综合题
一、解答题(本大题共3小题,共24.0分)
1.已知点P在线段AB上,点O在线段AB延长线上.以点O为圆心,OP为半径作圆,点C是圆O上的一点.
(1)如图,如果AP=2PB,PB=BO.求证:△CAO∽△BCO;
(2)如果AP=m(m是常数,且m>1),BP=1,OP是OA,OB的比例中项.当点C在圆O上运动时,求AC:BC的值(结果用含m的式子表示);
(3)在(2)的条件下,讨论以BC为半径的圆B和以CA为半径的圆C的位置关系,并写出相应m的取值范围.
2.如图,BD是⊙O的直径,OA⊥OB,M是劣弧上一点,过点M作⊙O的切线MP交OA的延长线于P点,MD与OA交于N点.
(1)求证:PM=PN;
(2)若BD=4,PA=AO,过点B作BC∥MP交⊙O于C点,求BC的长.
3、如图,在平面直角坐标系中,以坐标原点O为圆心,2为半径画⊙O,P是⊙O上一动点,且P在第一象限内,过点P作⊙O的切线与x轴相交于点A,与y轴相交于点B.
(1)点P在运动时,线段AB的长度也在发生变化,请写出线段AB长度的最小值,并说明理由;
(2)在⊙O上是否存在一点Q,使得以Q,O,A,P为顶点的四边形是平行四边形?若存在,请求出Q点的坐标;若不存在,请说明理由.
5、圆的内接四边形综合题
一、解答题(本大题共4小题,共32.0分)
1.如图,在Rt△ABC中,斜边BC=12,∠C=30°,D为BC的中点,△ABD的外接圆⊙O与AC交于F点,过A作⊙O的切线AE交DF的延长线于E点.
(1)求证:AE⊥DE;
(2)计算:AC?AF的值.
2.如图,⊙O为△ABC的外接圆,且AB=AC,过点A的直线交⊙O于D,交BC延长线于F,DE是BD的延长线,连接CD.
(1)求证:∠EDF=∠CDF;
(2)求证:AB2=AF?AD;
(3)若BD是⊙O的直径,且∠EDC=120°,BC=6cm,求AF的长.
如图,⊙C经过坐标原点,且与两坐标轴分别交于点A与点B,点A的坐标为(0,4),M是圆上一点,∠BMO=120°.
(1)求证:AB为⊙C直径;
(2)求⊙C的半径及圆心C的坐标.
4.如图所示,圆O是△ABC的外接圆,∠BAC与∠ABC的平分线相交于点I,延长AI交圆O于点D,连接BD、DC.
(1)求证:BD=DC=DI;
(2)若圆O的半径为10cm,∠BAC=120°,求△BDC的面积.
6、圆的其他的综合题
一、解答题(本大题共5小题,共40.0分)
1.如图,⊙O的半径为,⊙O的内接一个正多边形,边心距为1,求它的中心角、边长、面积.
2.如图,在扇形OAB中,∠AOB=90°,半径OA=6.将扇形OAB沿过点B的直线折叠,点O恰好落在上点D处,折痕交OA于点C,求整个阴影部分的周长和面积.
3.如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠D=30°.
(1)判断直线CD和⊙O的位置关系,并说明理由;
(2)若⊙O的半径为3,求的长.(结果保留π)
4.如图,已知△ABC,AC=BC=6,∠C=90度.O是AB的中点,⊙O与AC相切于点D、与BC相切于点E.设⊙O交OB于F,连DF并延长交CB的延长线于G.
(1)∠BFG与∠BGF是否相等?为什么?
(2)求由DG、GE和弧ED所围成图形的面积.(阴影部分)
5.如图,在△ABC中,∠ABC=90°,D是边AC上的一点,连接BD,使∠A=2∠1,E是BC上的一点,以BE为直径的⊙O经过点D.
(1)求证:AC是⊙O的切线;
(2)若∠A=60°,⊙O的半径为2,求阴影部分的面积.(结果保留根号和π)
6、如图,在Rt△ABC中,斜边BC=12,∠C=30°,D为BC的中点,△ABD的外接圆⊙O与AC交于F点,过A作⊙O的切线AE交DF的延长线于E点.
(1)求证:AE⊥DE;
(2)计算:AC?AF的值.
7、如图,⊙O为△ABC的外接圆,且AB=AC,过点A的直线交⊙O于D,交BC延长线于F,DE是BD的延长线,连接CD.
(1)求证:∠EDF=∠CDF;
(2)求证:AB2=AF?AD;
(3)若BD是⊙O的直径,且∠EDC=120°,BC=6cm,求AF的长.
8.如图,⊙C经过坐标原点,且与两坐标轴分别交于点A与点B,点A的坐标为(0,4),M是圆上一点,∠BMO=120°.
(1)求证:AB为⊙C直径;
(2)求⊙C的半径及圆心C的坐标.
9.如图所示,圆O是△ABC的外接圆,∠BAC与∠ABC的平分线相交于点I,延长AI交圆O于点D,连接BD、DC.
(1)求证:BD=DC=DI;
(2)若圆O的半径为10cm,∠BAC=120°,求△BDC的面积.
同课章节目录
