17.1.3 利用勾股定理作图课课练(含答案)
文档属性
| 名称 | 17.1.3 利用勾股定理作图课课练(含答案) | 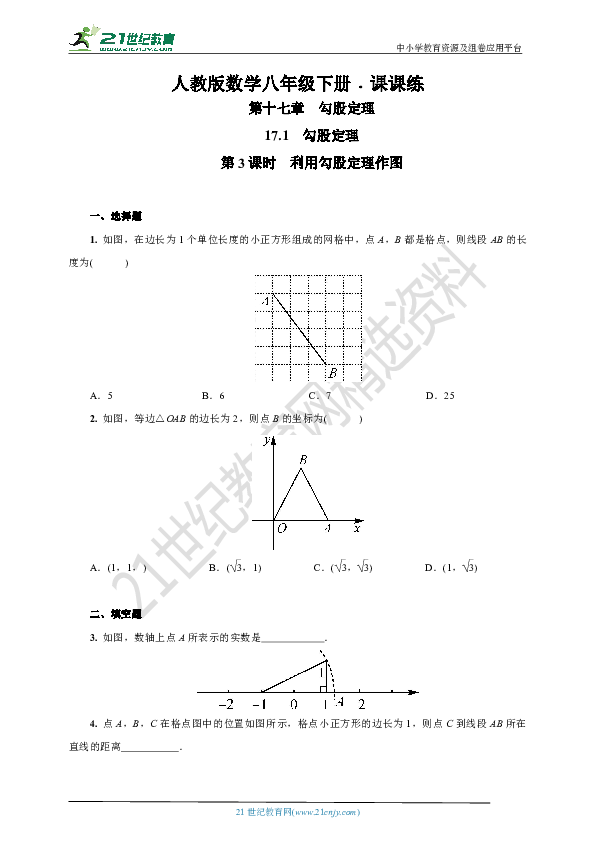 | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-29 15:03:32 | ||
图片预览



文档简介
人教版数学八年级下册﹒课课练
第十七章 勾股定理
17.1 勾股定理
第3课时 利用勾股定理作图
一、选择题
1. 如图,在边长为1个单位长度的小正方形组成的网格中,点A,B都是格点,则线段AB的长度为( )
A.5 B.6 C.7 D.25
2. 如图,等边△OAB的边长为2,则点B的坐标为( )
A.(1,1,) B.(,1) C.(,) D.(1,)
二、填空题
3. 如图,数轴上点A所表示的实数是 .
4. 点A,B,C在格点图中的位置如图所示,格点小正方形的边长为1,则点C到线段AB所在直线的距离 .
5. 如图,将边长为6 cm的正方形纸片ABCD折叠,使点D落在AB边中点E处,点C落在点Q处,折痕为FH,则线段AF的长是 cm.
三、解答题
6. 在数轴上作出表示的点(保留作图痕迹,不写作法).
7. 在△ABC中,AB=AC=13 cm,BC=10 cm,求等腰三角形的边上的高与面积.
8. 如图,△ABC和△DCE都是边长为4的等边三角形,点B,C,E在同一条直线上,连接BD,求BD的长.
9. 仔细观察图形,认真分析下列各式,然后解答问题.
OA=()2+1=2,S1=;
OA=()2+1=3,S2=;
OA=()2+1=4,S3=;
…
求:(1)请用含有n(n是正整数)的等式表示上述变化规律;
(2)推算出OA10的长;
(3)求出S+S+S+…+S的值.
参 考 答 案
1. A 2. D
3. -1
4.
5.
6. 解:略.
7. 解:过点A作AD⊥BC于点D,∵AB=AC=13 cm,∴BD=CD=BC=×10=5(cm).∴AD===12(cm).∴S△ABC=BC·AD=×10×12=60(cm2).
8. 解:∵△ABC和△DCE都是边长为4的等边三角形,∴CB=CD,∠CDE=∠DCE=60°. ∴∠BDC
=∠DBC=∠DCE=30°. ∴∠BDE=90°. 在Rt△BDE中,DE=4,BE=8,DB==
=4.
9. 解:(1)OA=()2+1=n,Sn=(n为正整数).
(2)OA=()2+1=10,∴OA10=.
(3)S+S+S+…+S=()2+()2+()2+…+()2+()2=+++…++===.
第十七章 勾股定理
17.1 勾股定理
第3课时 利用勾股定理作图
一、选择题
1. 如图,在边长为1个单位长度的小正方形组成的网格中,点A,B都是格点,则线段AB的长度为( )
A.5 B.6 C.7 D.25
2. 如图,等边△OAB的边长为2,则点B的坐标为( )
A.(1,1,) B.(,1) C.(,) D.(1,)
二、填空题
3. 如图,数轴上点A所表示的实数是 .
4. 点A,B,C在格点图中的位置如图所示,格点小正方形的边长为1,则点C到线段AB所在直线的距离 .
5. 如图,将边长为6 cm的正方形纸片ABCD折叠,使点D落在AB边中点E处,点C落在点Q处,折痕为FH,则线段AF的长是 cm.
三、解答题
6. 在数轴上作出表示的点(保留作图痕迹,不写作法).
7. 在△ABC中,AB=AC=13 cm,BC=10 cm,求等腰三角形的边上的高与面积.
8. 如图,△ABC和△DCE都是边长为4的等边三角形,点B,C,E在同一条直线上,连接BD,求BD的长.
9. 仔细观察图形,认真分析下列各式,然后解答问题.
OA=()2+1=2,S1=;
OA=()2+1=3,S2=;
OA=()2+1=4,S3=;
…
求:(1)请用含有n(n是正整数)的等式表示上述变化规律;
(2)推算出OA10的长;
(3)求出S+S+S+…+S的值.
参 考 答 案
1. A 2. D
3. -1
4.
5.
6. 解:略.
7. 解:过点A作AD⊥BC于点D,∵AB=AC=13 cm,∴BD=CD=BC=×10=5(cm).∴AD===12(cm).∴S△ABC=BC·AD=×10×12=60(cm2).
8. 解:∵△ABC和△DCE都是边长为4的等边三角形,∴CB=CD,∠CDE=∠DCE=60°. ∴∠BDC
=∠DBC=∠DCE=30°. ∴∠BDE=90°. 在Rt△BDE中,DE=4,BE=8,DB==
=4.
9. 解:(1)OA=()2+1=n,Sn=(n为正整数).
(2)OA=()2+1=10,∴OA10=.
(3)S+S+S+…+S=()2+()2+()2+…+()2+()2=+++…++===.
