人教版 七年级数学下册7.1.2平面直角坐标系 课件(41张)
文档属性
| 名称 | 人教版 七年级数学下册7.1.2平面直角坐标系 课件(41张) |

|
|
| 格式 | zip | ||
| 文件大小 | 866.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-29 00:00:00 | ||
图片预览



文档简介
(共41张PPT)
在平面内确定物体的位置一般需要几个数据?怎样利用有序数对表示点的位置?
新课导入
想一想
如图:是某市旅游景点示意图,如果把 “人民广场”的位置作为起点,记为(0,0); 分别记向北,向东为正.
?
?
灵石塔
鼓楼
?
北
人民广场
会展中心
龙珠湖
镇海楼
?
玉泉
?
?
?
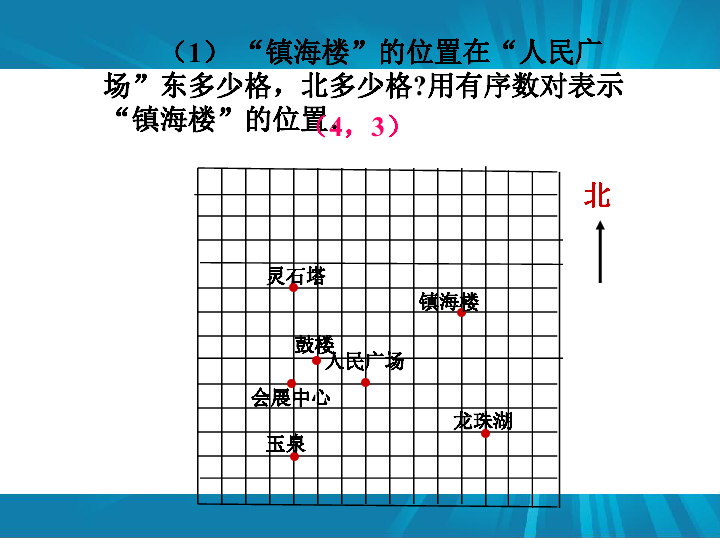
(1) “镇海楼”的位置在“人民广场”东多少格,北多少格?用有序数对表示“镇海楼”的位置.
(4,3)
?
?
灵石塔
鼓楼
?
北
人民广场
会展中心
龙珠湖
镇海楼
?
玉泉
?
?
?
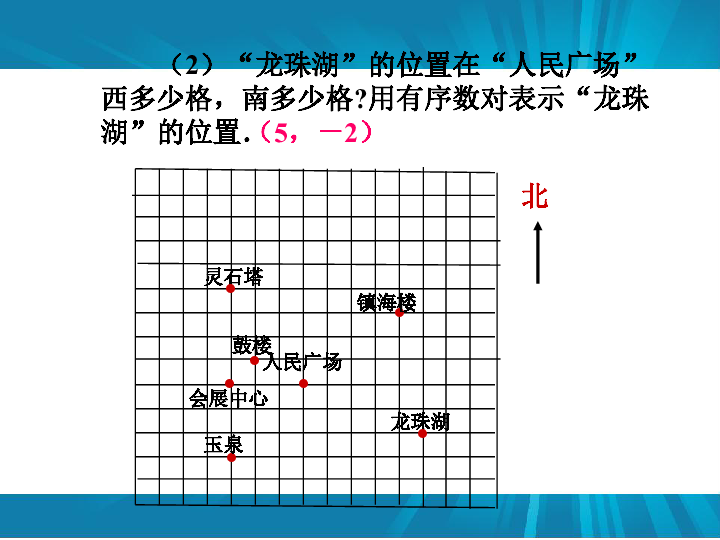
(2)“龙珠湖”的位置在“人民广场”西多少格,南多少格?用有序数对表示“龙珠湖”的位置.
(5,-2)
?
?
灵石塔
鼓楼
?
北
人民广场
会展中心
龙珠湖
镇海楼
?
玉泉
?
?
?
(3)“灵石塔”的位置在“人民广场”西多少格,北多少格?怎样用有序数对表示“灵石塔”的位置?
(-3,4)
?
?
灵石塔
鼓楼
?
北
人民广场
会展中心
龙珠湖
镇海楼
?
玉泉
?
?
?
7.1.2 平面直角坐标系
讲授新课
知识与能力
1.认识平面直角坐标系,了解点与坐标的对应关系;
2.在给定的直角坐标系中,能根据坐标描出点的位置,能由点的位置写出点的坐标.
教学目标
过程与方法
经历画直角坐标系,由点找坐标等过程,发展数形结合意识,合作交流意识,培养创新能力.
情感态度与价值观
培养细致认真的学习习惯.通过介绍笛卡儿创立坐标系的背景知识,激励自己敢于探索,勇攀科学高峰.
教学目标
重点
掌握由平面上的点确定其坐标,由坐标确定其在平面上的点.
难点
了解点与坐标的对应关系,体会数形结合思想.
教学重难点
法国数学家笛卡儿
最早引入坐标系,用代数方法研究几何图形.笛卡儿是近代科学的始祖.笛卡儿是欧洲近代哲学的奠基人之一,黑格尔称他为“现代哲学之父”.同时,他又是一位勇于探索的科学家,他所建立的解析几何在数学史上具有划时代的意义.
数轴上的点A表示数-3.反过来,数-3就是点A的位置.
因此我们可以说-3是点A在数轴上的坐标.
●
●
●
●
●
A
B
C
D
F
-3 -2 -1 0 1 2 3 4
数轴上的点与实数之间存在着一一对应的关系.
点B在数轴上的坐标是 ;
点C在数轴上的坐标是 ;
点D在数轴上的坐标是 ;
点E在数轴上的坐标是 .
-1.5
0
2
3
●
●
●
●
●
A
B
C
D
F
-3 -2 -1 0 1 2 3 4
·A
·D
·B
·C
如果借助数轴,怎样来表示平面内的点呢?
·A
·D
·B
·C
0 1 2 3 4 5 6 7 8 9 10
10
9
8
7
6
5
4
3
2
1
(2,1)
(4,3)
(4,6)
(8,8)
·A
·D
·B
0 1 2 3 4 5 6 7 8 9 10
9
8
7
6
5
4
3
2
1
·C
(8,7)
(4,5)
(4,2)
(2,0)
0 1 2 3 4 5 6 7 8 9 10
·A
·D
·B
·C
2
1
-1
-2
-3
-4
-5
-6
-7
-8
(2,-7)
(4,-5)
(4,-2)
(8,0)
在平面内有公共原点而且互相垂直的两条数轴,就构成了平面直角坐标系.简称直角坐标系,坐标系所在的平面就叫做坐标平面.
知识要点
x
横轴
0
1
2
3
4
5
-4
-3
-2
-1
3
1
4
2
5
-2
-4
-1
-3
y
纵轴
原点
平面直角坐标系
(1)两条数轴互相垂直;
(2)两条数轴的原点重合;
(3)通常分别取x、y轴向右、向上为正方向;
(4)两条数轴的单位长度一般取相同的.
建立平面直角坐标系时要注意:
注意
下面四个图形中,哪一个属于平面直角坐标系?
3
2
1
-1
-2
-3
-3 -2 -1 1 2 3
x
0
y
-3 -2 -1 1 2 3
3
2
1
-1
-2
-3
y
0
x
2
1
-1
-2
3 2 1 -1 -2 -3
x
y
0
3
2
1
-1
-2
-3
x
y
-3 -2 -1 1 2 3
0
·
A
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
·
B
B(-3,2)
·
D
(3,-3)
如何表示点A的位置:
过点A作x轴的垂线,垂足在x轴上对应的数是2,就是点A的横坐标.
过点A作y轴的垂线,垂足在y轴上对应的数是3,就是点A的纵坐标.
有序数对(2,3)就是点A的坐标.记作:A(2,3)
(2, 3)
x轴上的坐标
写在前面
坐标是有序
的数对
对于坐标平面内的任意一点,都可以找到一个有序实数对(x,y)和它对应.
这个有序实数对(x,y)就是这个点的坐标.
点的坐标
知识要点
·
B
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
·
C
·
A
·
E
·
D
( 2,4 )
( 4,2 )
(-3,2 )
(-2,-3 )
( 3,-2 )
例1 写出图中A、B、C、D、E各点的坐标.
x
横轴
y
纵轴
原点
第一象限
第四象限
第三象限
第二象限
注意:坐标轴上的点不属于任何象限.
0
1
2
3
4
5
-4
-3
-2
-1
3
1
4
2
5
-2
-4
-1
-3
(-,+)
(+,+)
(-,-)
(+,-)
A(3,6)
B(0,-8)
C(-7,-5)
D(-6,0)
E(-3.6,5)
F(5,-6)
G(0,0)
第一象限
第三象限
第二象限
第四象限
y轴上
x轴上
原点
下列各点分别在坐标平面的什么位置上?
当x>0,y>0时,在第一象限内;
当x<0,y>0时,在第二象限内;
当x<0,y<0时,在第三象限内;
当x>0,y<0时,在第四象限内.
平面直角坐标系内有一点P(x,y),且x≠0,y≠0,说一说P点的什么位置?
设点M(a,b)为平面直角坐标系中的点.
当a>0,b<0时点M位于第 象限;
当ab>0时,点M位于第 象限;
当a为任意数时,且b<0时,点M直角坐标系中可能的的位置是 ;
四
一或三
第四象限或第三象限或y轴
练一练
1.原点O的坐标是什么?
2.x轴与y轴上的点的坐标有什么特点?
想一想
任何一个在x轴上的点的纵坐标都为0,记作(x,0).
由此得出:任何一个在y轴上的点的横坐标为0,记作(0,y).
原点的坐标为(0,0);
5
-5
-2
-3
-4
-1
3
2
4
1
-6
6
y
-5
5
-3
-4
4
-2
3
-1
2
1
-6
6
o
x
x轴上的点,纵坐标都是0;
·
·
·
·
A
B
C
A(-4,0)
B(4,0)
O(0,0)
C(6,0)
·
·
·
D
E
F
D(0,4)
y轴上的点,横坐标都是0.
O(0,0)
E(0,-3)
F(0,-5)
O
写出下列各点的坐标.
若设点P(x,y),
则:P点关于x轴的对称点P1( x,-y)
P点关于y轴的对称点P2( -x, y),
P点关于原点O的对称点P3(-x,-y)
归纳
例2.在下图的直角坐标系中描出下列各组点,并将各组内的线段依次连接起来.
(1) (2,0), (4,0), (6,2), (6,6), (5,8), (4,6), (2,6), (1,8), (0,6), (0,2), (2,0);
(2) (1,3), (2,2), (4,2), (5,3);
(3) (1,4), (2,4), (2,5), (1,5), (1,4);
(4) (4,4), (5,4), (5,5), (4,5), (4,4); (5) (3,3).
o
2
4
6
8
2
4
6
8
y
x
观察所得的图形,你觉得它像什么?
猫脸
例3 在平面直角坐标系内,A(-3,4),B(-1,2),O为原点,求三角形AOB的面积.
解:作辅助线AE⊥y轴于E,
BE⊥y轴于D.
S△AOE=0.5×AE×OE
=0.5×3×4=6
S△BOD=0.5×BD×OD
=0.5×1×(3-1)
=1
S梯形ADBE =0.5×(BD+AE) ×DE
=0.5×(1+3)×(4-2)=4
S△AOB =6-1-4=1
答:三角形AOB的面积为1.
┓
┓
例4 已知点P(6-2a,3a-4)到x轴和y轴的距离相等,求a的值.
解:因为点P到x轴和y轴的距离相等,
所以6-2a=3a-4
a=2
答:a的值为2.
求点的坐标时注意事项
(1)要先找横坐标,后找纵坐标,即“先横后纵”;
(2)坐标有正负之分,四个象限内点的坐标的符号特征要牢记;
(3)对于坐标轴上的点,x轴上的点是纵坐标为0,即(x,0);y轴上的点是横坐标为0,即(0,y);
(4)坐标书写不规范,记得写括号和逗号.
归纳
有关概念
平面直角坐标系
y轴
x轴
原点
坐标平面
坐标平面内点的坐标
横坐标
纵坐标
课堂小结
1.四个象限的点的横纵坐标的符号:
第一象限(+,+) 第二象限(—,+)
第三象限(—,—)第四象限(+,—)
2.x轴上的点的纵坐标为0,表示为(x,0)
y轴上的点的横坐标为0,表示为(0,y)
3.关于X轴、Y轴、原点对称的点横纵坐标的关系:
关于X轴对称的两点,横坐标相等,纵坐标互为相反数;
关于Y轴对称的两点,横坐标互为相反数,纵坐标相等;
关于原点对称的两点,横坐标、纵坐标互为相反数.
1.点(5,-3)在第_____象限;点(-4,-6)在第_______象限;点(0,6)在____轴上;
若点(a+3,-5)在y轴上,则a=______.
四
三
y
-3
2.点 M(-13,5)到 x轴的距离是_________,到 y轴的距离是________.
13
5
随堂练习
3.若点(a,b-4)在第二象限,则a的取值范围是_____,b的取值范围________.
4.实数 x,y满足 (x+1)2+ |y| = 0,则点 P( x,y)在( )
A.原点 B.x轴负半轴
C.第一象限 D.任意位置
a<0
b>4
B
5.直角坐标系中有一点 M(a,b),其中ab=0 ,则点M的位置在( )
A.原点 B.x轴上
C.y轴上 D.坐标轴上
D
6.如果点M(3a-9,1-a)在第三象限,且它的坐标都是整数,则M点的坐标为__________.
(-3,-1)
在平面内确定物体的位置一般需要几个数据?怎样利用有序数对表示点的位置?
新课导入
想一想
如图:是某市旅游景点示意图,如果把 “人民广场”的位置作为起点,记为(0,0); 分别记向北,向东为正.
?
?
灵石塔
鼓楼
?
北
人民广场
会展中心
龙珠湖
镇海楼
?
玉泉
?
?
?
(1) “镇海楼”的位置在“人民广场”东多少格,北多少格?用有序数对表示“镇海楼”的位置.
(4,3)
?
?
灵石塔
鼓楼
?
北
人民广场
会展中心
龙珠湖
镇海楼
?
玉泉
?
?
?
(2)“龙珠湖”的位置在“人民广场”西多少格,南多少格?用有序数对表示“龙珠湖”的位置.
(5,-2)
?
?
灵石塔
鼓楼
?
北
人民广场
会展中心
龙珠湖
镇海楼
?
玉泉
?
?
?
(3)“灵石塔”的位置在“人民广场”西多少格,北多少格?怎样用有序数对表示“灵石塔”的位置?
(-3,4)
?
?
灵石塔
鼓楼
?
北
人民广场
会展中心
龙珠湖
镇海楼
?
玉泉
?
?
?
7.1.2 平面直角坐标系
讲授新课
知识与能力
1.认识平面直角坐标系,了解点与坐标的对应关系;
2.在给定的直角坐标系中,能根据坐标描出点的位置,能由点的位置写出点的坐标.
教学目标
过程与方法
经历画直角坐标系,由点找坐标等过程,发展数形结合意识,合作交流意识,培养创新能力.
情感态度与价值观
培养细致认真的学习习惯.通过介绍笛卡儿创立坐标系的背景知识,激励自己敢于探索,勇攀科学高峰.
教学目标
重点
掌握由平面上的点确定其坐标,由坐标确定其在平面上的点.
难点
了解点与坐标的对应关系,体会数形结合思想.
教学重难点
法国数学家笛卡儿
最早引入坐标系,用代数方法研究几何图形.笛卡儿是近代科学的始祖.笛卡儿是欧洲近代哲学的奠基人之一,黑格尔称他为“现代哲学之父”.同时,他又是一位勇于探索的科学家,他所建立的解析几何在数学史上具有划时代的意义.
数轴上的点A表示数-3.反过来,数-3就是点A的位置.
因此我们可以说-3是点A在数轴上的坐标.
●
●
●
●
●
A
B
C
D
F
-3 -2 -1 0 1 2 3 4
数轴上的点与实数之间存在着一一对应的关系.
点B在数轴上的坐标是 ;
点C在数轴上的坐标是 ;
点D在数轴上的坐标是 ;
点E在数轴上的坐标是 .
-1.5
0
2
3
●
●
●
●
●
A
B
C
D
F
-3 -2 -1 0 1 2 3 4
·A
·D
·B
·C
如果借助数轴,怎样来表示平面内的点呢?
·A
·D
·B
·C
0 1 2 3 4 5 6 7 8 9 10
10
9
8
7
6
5
4
3
2
1
(2,1)
(4,3)
(4,6)
(8,8)
·A
·D
·B
0 1 2 3 4 5 6 7 8 9 10
9
8
7
6
5
4
3
2
1
·C
(8,7)
(4,5)
(4,2)
(2,0)
0 1 2 3 4 5 6 7 8 9 10
·A
·D
·B
·C
2
1
-1
-2
-3
-4
-5
-6
-7
-8
(2,-7)
(4,-5)
(4,-2)
(8,0)
在平面内有公共原点而且互相垂直的两条数轴,就构成了平面直角坐标系.简称直角坐标系,坐标系所在的平面就叫做坐标平面.
知识要点
x
横轴
0
1
2
3
4
5
-4
-3
-2
-1
3
1
4
2
5
-2
-4
-1
-3
y
纵轴
原点
平面直角坐标系
(1)两条数轴互相垂直;
(2)两条数轴的原点重合;
(3)通常分别取x、y轴向右、向上为正方向;
(4)两条数轴的单位长度一般取相同的.
建立平面直角坐标系时要注意:
注意
下面四个图形中,哪一个属于平面直角坐标系?
3
2
1
-1
-2
-3
-3 -2 -1 1 2 3
x
0
y
-3 -2 -1 1 2 3
3
2
1
-1
-2
-3
y
0
x
2
1
-1
-2
3 2 1 -1 -2 -3
x
y
0
3
2
1
-1
-2
-3
x
y
-3 -2 -1 1 2 3
0
·
A
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
·
B
B(-3,2)
·
D
(3,-3)
如何表示点A的位置:
过点A作x轴的垂线,垂足在x轴上对应的数是2,就是点A的横坐标.
过点A作y轴的垂线,垂足在y轴上对应的数是3,就是点A的纵坐标.
有序数对(2,3)就是点A的坐标.记作:A(2,3)
(2, 3)
x轴上的坐标
写在前面
坐标是有序
的数对
对于坐标平面内的任意一点,都可以找到一个有序实数对(x,y)和它对应.
这个有序实数对(x,y)就是这个点的坐标.
点的坐标
知识要点
·
B
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
·
C
·
A
·
E
·
D
( 2,4 )
( 4,2 )
(-3,2 )
(-2,-3 )
( 3,-2 )
例1 写出图中A、B、C、D、E各点的坐标.
x
横轴
y
纵轴
原点
第一象限
第四象限
第三象限
第二象限
注意:坐标轴上的点不属于任何象限.
0
1
2
3
4
5
-4
-3
-2
-1
3
1
4
2
5
-2
-4
-1
-3
(-,+)
(+,+)
(-,-)
(+,-)
A(3,6)
B(0,-8)
C(-7,-5)
D(-6,0)
E(-3.6,5)
F(5,-6)
G(0,0)
第一象限
第三象限
第二象限
第四象限
y轴上
x轴上
原点
下列各点分别在坐标平面的什么位置上?
当x>0,y>0时,在第一象限内;
当x<0,y>0时,在第二象限内;
当x<0,y<0时,在第三象限内;
当x>0,y<0时,在第四象限内.
平面直角坐标系内有一点P(x,y),且x≠0,y≠0,说一说P点的什么位置?
设点M(a,b)为平面直角坐标系中的点.
当a>0,b<0时点M位于第 象限;
当ab>0时,点M位于第 象限;
当a为任意数时,且b<0时,点M直角坐标系中可能的的位置是 ;
四
一或三
第四象限或第三象限或y轴
练一练
1.原点O的坐标是什么?
2.x轴与y轴上的点的坐标有什么特点?
想一想
任何一个在x轴上的点的纵坐标都为0,记作(x,0).
由此得出:任何一个在y轴上的点的横坐标为0,记作(0,y).
原点的坐标为(0,0);
5
-5
-2
-3
-4
-1
3
2
4
1
-6
6
y
-5
5
-3
-4
4
-2
3
-1
2
1
-6
6
o
x
x轴上的点,纵坐标都是0;
·
·
·
·
A
B
C
A(-4,0)
B(4,0)
O(0,0)
C(6,0)
·
·
·
D
E
F
D(0,4)
y轴上的点,横坐标都是0.
O(0,0)
E(0,-3)
F(0,-5)
O
写出下列各点的坐标.
若设点P(x,y),
则:P点关于x轴的对称点P1( x,-y)
P点关于y轴的对称点P2( -x, y),
P点关于原点O的对称点P3(-x,-y)
归纳
例2.在下图的直角坐标系中描出下列各组点,并将各组内的线段依次连接起来.
(1) (2,0), (4,0), (6,2), (6,6), (5,8), (4,6), (2,6), (1,8), (0,6), (0,2), (2,0);
(2) (1,3), (2,2), (4,2), (5,3);
(3) (1,4), (2,4), (2,5), (1,5), (1,4);
(4) (4,4), (5,4), (5,5), (4,5), (4,4); (5) (3,3).
o
2
4
6
8
2
4
6
8
y
x
观察所得的图形,你觉得它像什么?
猫脸
例3 在平面直角坐标系内,A(-3,4),B(-1,2),O为原点,求三角形AOB的面积.
解:作辅助线AE⊥y轴于E,
BE⊥y轴于D.
S△AOE=0.5×AE×OE
=0.5×3×4=6
S△BOD=0.5×BD×OD
=0.5×1×(3-1)
=1
S梯形ADBE =0.5×(BD+AE) ×DE
=0.5×(1+3)×(4-2)=4
S△AOB =6-1-4=1
答:三角形AOB的面积为1.
┓
┓
例4 已知点P(6-2a,3a-4)到x轴和y轴的距离相等,求a的值.
解:因为点P到x轴和y轴的距离相等,
所以6-2a=3a-4
a=2
答:a的值为2.
求点的坐标时注意事项
(1)要先找横坐标,后找纵坐标,即“先横后纵”;
(2)坐标有正负之分,四个象限内点的坐标的符号特征要牢记;
(3)对于坐标轴上的点,x轴上的点是纵坐标为0,即(x,0);y轴上的点是横坐标为0,即(0,y);
(4)坐标书写不规范,记得写括号和逗号.
归纳
有关概念
平面直角坐标系
y轴
x轴
原点
坐标平面
坐标平面内点的坐标
横坐标
纵坐标
课堂小结
1.四个象限的点的横纵坐标的符号:
第一象限(+,+) 第二象限(—,+)
第三象限(—,—)第四象限(+,—)
2.x轴上的点的纵坐标为0,表示为(x,0)
y轴上的点的横坐标为0,表示为(0,y)
3.关于X轴、Y轴、原点对称的点横纵坐标的关系:
关于X轴对称的两点,横坐标相等,纵坐标互为相反数;
关于Y轴对称的两点,横坐标互为相反数,纵坐标相等;
关于原点对称的两点,横坐标、纵坐标互为相反数.
1.点(5,-3)在第_____象限;点(-4,-6)在第_______象限;点(0,6)在____轴上;
若点(a+3,-5)在y轴上,则a=______.
四
三
y
-3
2.点 M(-13,5)到 x轴的距离是_________,到 y轴的距离是________.
13
5
随堂练习
3.若点(a,b-4)在第二象限,则a的取值范围是_____,b的取值范围________.
4.实数 x,y满足 (x+1)2+ |y| = 0,则点 P( x,y)在( )
A.原点 B.x轴负半轴
C.第一象限 D.任意位置
a<0
b>4
B
5.直角坐标系中有一点 M(a,b),其中ab=0 ,则点M的位置在( )
A.原点 B.x轴上
C.y轴上 D.坐标轴上
D
6.如果点M(3a-9,1-a)在第三象限,且它的坐标都是整数,则M点的坐标为__________.
(-3,-1)
