沪科版七年级数学下册 第八章 整式乘法与因式分解(8.2-8.3)同步练习(含答案)
文档属性
| 名称 | 沪科版七年级数学下册 第八章 整式乘法与因式分解(8.2-8.3)同步练习(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 31.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
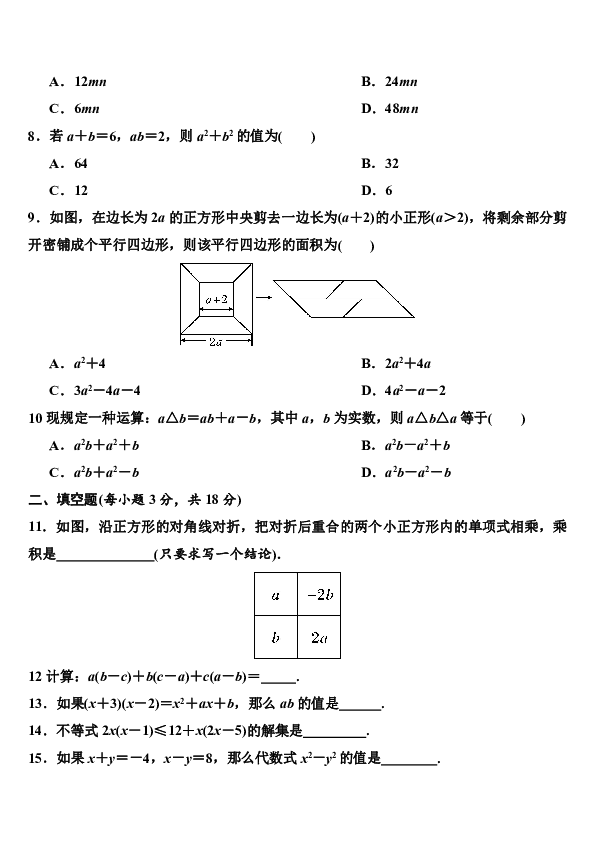
| 科目 | 数学 | ||
| 更新时间 | 2020-02-29 00:00:00 | ||
图片预览


文档简介
沪科版数学七年级下册
第八章 整式乘法与因式分解
(8.2-8.3)
一、选择题(每小题3分,共30分)
1.下列运算正确的是( )
A.a2+a3=a5 B.(-2a3)3=-6a6
C.(2a+1)(2a-1)=2a2-1 D.(2a3-a2)÷a2=2a-1
2.单项式乘以多项式依据的运算律是( )
A.加法结合律 B.加法交换律
C.乘法结合律 D.乘法分配律
3.计算(-xy)3·(7xy2-9x2y)的结果正确的是( )
A.-7x2y5+9x3y4 B.-7x2y5-9x3y4
C.-7x4y5+9x5y4 D.7x4y5+9x5y4
4.下列计算正确的是( )
A.-3x2y·5x2y=2x2y B.-2x2y3·2x3y=-2x5y4
C.35x3y2÷5x2y=7xy D.(-2x-y)(2x+y)=4x2-y2
5.当a=-1时,代数式(a+1)2+a(a-3)的值等于( )
A.-4 B.4
C.-2 D.2
6.如果(x-a)(x-b)的积中不含有x的一次项,那么a,b的关系是( )
A.互为倒数 B.互为相反数
C.相等 D.积为零
7.设(3m+2n)2=(3m-2n)2+P,则P的值是( )
A.12mn B.24mn
C.6mn D.48mn
8.若a+b=6,ab=2,则a2+b2的值为( )
A.64 B.32
C.12 D.6
9.如图,在边长为2a的正方形中央剪去一边长为(a+2)的小正形(a>2),将剩余部分剪开密铺成个平行四边形,则该平行四边形的面积为( )
A.a2+4 B.2a2+4a
C.3a2-4a-4 D.4a2-a-2
10现规定一种运算:a△b=ab+a-b,其中a,b为实数,则a△b△a等于( )
A.a2b+a2+b B.a2b-a2+b
C.a2b+a2-b D.a2b-a2-b
二、填空题(每小题3分,共18分)
11.如图,沿正方形的对角线对折,把对折后重合的两个小正方形内的单项式相乘,乘积是 (只要求写一个结论).
12计算:a(b-c)+b(c-a)+c(a-b)= .
13.如果(x+3)(x-2)=x2+ax+b,那么ab的值是 .
14.不等式2x(x-1)≤12+x(2x-5)的解集是 .
15.如果x+y=-4,x-y=8,那么代数式x2-y2的值是 .
16.若一个长方体的长,宽,高分别为3a+2,3a-2,a,则这个长方体的表面积为 .
三、解答题(共52分)
17. (12分)计算:
(1)(x-xy)·(-12y); (2)(a+2b-c)(a-2b-c);
(3)a3b4c2÷(-ab2); (4)3(a+b)5÷2(a+b)3.
18. (5分)计算:(a+3)(a-3)+a(4-a).
19. (6分)先化简,再求值:(a+2b)2+(b+a)(b-a),其中a=-1,b=2.
20. (10分)用简便方法计算:
(1)1.02×0.98; (2)20182-2017×2019.
21. (9分)在(x2+ax+b)(2x2-3x-1)的计算结果中,x3的系数是-5,x2的系数是-6,求a、b的值.
22. (10分)有足够多的长方形和正方形卡片,如图所示.
(1)如果选取1号、2号、3号卡片分别为1张、2张、3张,可拼成一个长方形(不重叠无缝隙),请画出这个长方形的草图,并运用拼图前后面积之间的关系写出一个等式;
(2)小明想用类似的方法解释多项式乘法(a+3b)(2a+b)=2a2+7ab+3b2,那么需用2号卡片 张,3号卡片 张.
答案
1-5:DDCCB 6-10:BBBCC
11、2a2或-2b2
12、0
13、-6
14、x≤4
15、-32
16、30a2-8
17、(1)解:原式=-4xy+9xy2;
(2)解:原式=a2+c2-4b2-2ac;
(3)解:原式=-a2b2c2;
(4)原式=a2+3ab+b2.
18、解:原式=a2-9+4a-a2=4a-9.
19、解:原式=a2+4ab+4b2+b2-a2=4ab+5b2.当a=-1,b=2时,原式=4×(-1)×2+5×22=-8+20=12.
20、(1)解:原式=(1+0.02)(1-0.02)=1-0.0004=0.9996;
(2)解:原式=20182-(2018-1)×(2018+1)=20182-(20182-1)=1.
21、解:(x2+ax+b)(2x2-3x-1)=2x4+(-3+2a)x3+(-1-3a+2b)x2-ax-3bx-b,因为x3的系数是-5,x2的系数是-6,所以-3+2a=-5,-1-3a+2b=-6,解得a=-1,b=-4.
22、解:如图:(1)如图所示:等式为(a+b)(a+2b)=a2+3ab+2b2;
(2)因为(a+3b)(2a+b)=2a2+ab+6ab+3b2=2a2+7ab+3b2,所以需用2号卡片3张,3号卡片7张,故答案为3,7.
第八章 整式乘法与因式分解
(8.2-8.3)
一、选择题(每小题3分,共30分)
1.下列运算正确的是( )
A.a2+a3=a5 B.(-2a3)3=-6a6
C.(2a+1)(2a-1)=2a2-1 D.(2a3-a2)÷a2=2a-1
2.单项式乘以多项式依据的运算律是( )
A.加法结合律 B.加法交换律
C.乘法结合律 D.乘法分配律
3.计算(-xy)3·(7xy2-9x2y)的结果正确的是( )
A.-7x2y5+9x3y4 B.-7x2y5-9x3y4
C.-7x4y5+9x5y4 D.7x4y5+9x5y4
4.下列计算正确的是( )
A.-3x2y·5x2y=2x2y B.-2x2y3·2x3y=-2x5y4
C.35x3y2÷5x2y=7xy D.(-2x-y)(2x+y)=4x2-y2
5.当a=-1时,代数式(a+1)2+a(a-3)的值等于( )
A.-4 B.4
C.-2 D.2
6.如果(x-a)(x-b)的积中不含有x的一次项,那么a,b的关系是( )
A.互为倒数 B.互为相反数
C.相等 D.积为零
7.设(3m+2n)2=(3m-2n)2+P,则P的值是( )
A.12mn B.24mn
C.6mn D.48mn
8.若a+b=6,ab=2,则a2+b2的值为( )
A.64 B.32
C.12 D.6
9.如图,在边长为2a的正方形中央剪去一边长为(a+2)的小正形(a>2),将剩余部分剪开密铺成个平行四边形,则该平行四边形的面积为( )
A.a2+4 B.2a2+4a
C.3a2-4a-4 D.4a2-a-2
10现规定一种运算:a△b=ab+a-b,其中a,b为实数,则a△b△a等于( )
A.a2b+a2+b B.a2b-a2+b
C.a2b+a2-b D.a2b-a2-b
二、填空题(每小题3分,共18分)
11.如图,沿正方形的对角线对折,把对折后重合的两个小正方形内的单项式相乘,乘积是 (只要求写一个结论).
12计算:a(b-c)+b(c-a)+c(a-b)= .
13.如果(x+3)(x-2)=x2+ax+b,那么ab的值是 .
14.不等式2x(x-1)≤12+x(2x-5)的解集是 .
15.如果x+y=-4,x-y=8,那么代数式x2-y2的值是 .
16.若一个长方体的长,宽,高分别为3a+2,3a-2,a,则这个长方体的表面积为 .
三、解答题(共52分)
17. (12分)计算:
(1)(x-xy)·(-12y); (2)(a+2b-c)(a-2b-c);
(3)a3b4c2÷(-ab2); (4)3(a+b)5÷2(a+b)3.
18. (5分)计算:(a+3)(a-3)+a(4-a).
19. (6分)先化简,再求值:(a+2b)2+(b+a)(b-a),其中a=-1,b=2.
20. (10分)用简便方法计算:
(1)1.02×0.98; (2)20182-2017×2019.
21. (9分)在(x2+ax+b)(2x2-3x-1)的计算结果中,x3的系数是-5,x2的系数是-6,求a、b的值.
22. (10分)有足够多的长方形和正方形卡片,如图所示.
(1)如果选取1号、2号、3号卡片分别为1张、2张、3张,可拼成一个长方形(不重叠无缝隙),请画出这个长方形的草图,并运用拼图前后面积之间的关系写出一个等式;
(2)小明想用类似的方法解释多项式乘法(a+3b)(2a+b)=2a2+7ab+3b2,那么需用2号卡片 张,3号卡片 张.
答案
1-5:DDCCB 6-10:BBBCC
11、2a2或-2b2
12、0
13、-6
14、x≤4
15、-32
16、30a2-8
17、(1)解:原式=-4xy+9xy2;
(2)解:原式=a2+c2-4b2-2ac;
(3)解:原式=-a2b2c2;
(4)原式=a2+3ab+b2.
18、解:原式=a2-9+4a-a2=4a-9.
19、解:原式=a2+4ab+4b2+b2-a2=4ab+5b2.当a=-1,b=2时,原式=4×(-1)×2+5×22=-8+20=12.
20、(1)解:原式=(1+0.02)(1-0.02)=1-0.0004=0.9996;
(2)解:原式=20182-(2018-1)×(2018+1)=20182-(20182-1)=1.
21、解:(x2+ax+b)(2x2-3x-1)=2x4+(-3+2a)x3+(-1-3a+2b)x2-ax-3bx-b,因为x3的系数是-5,x2的系数是-6,所以-3+2a=-5,-1-3a+2b=-6,解得a=-1,b=-4.
22、解:如图:(1)如图所示:等式为(a+b)(a+2b)=a2+3ab+2b2;
(2)因为(a+3b)(2a+b)=2a2+ab+6ab+3b2=2a2+7ab+3b2,所以需用2号卡片3张,3号卡片7张,故答案为3,7.
