人教版高中数学选修1-1《3.3.1函数的单调性与导数》导学案(Word版)
文档属性
| 名称 | 人教版高中数学选修1-1《3.3.1函数的单调性与导数》导学案(Word版) |
|
|
| 格式 | zip | ||
| 文件大小 | 73.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-02 16:26:04 | ||
图片预览

文档简介
2.25导学案
1.3.1函数的单调性与导数(第1课时)
【学习目标】
理解函数单调性和导数的关系.
2、会利用导数判断函数的单调性.
【重点难点】
重点:函数的单调性和导数的关系.
难点:利用导数判断函数的单调性.
【知识回顾】
回顾函数单调性的定义.
2、利用定义判断的单调性.
【问题探究】
知识点一、函数单调性和导数的关系
问题1:如上图(1),它表示跳水运动中高度随时间变化的函数的图像,
图(2)表示高台跳水运动员的速度随时间变化的函数的图像 运动员从起跳到最高点,以及从最高点到入水这两段时间的运动状态有什么区别?
问题2:
(1)运动员从起点到最高点,离水面的高度随时间的增加而 ,即是增函数.相应地, 0
(2)从最高点到入水,运动员离水面的高度随时间的增加而 ,即是减函数.相应地, 0
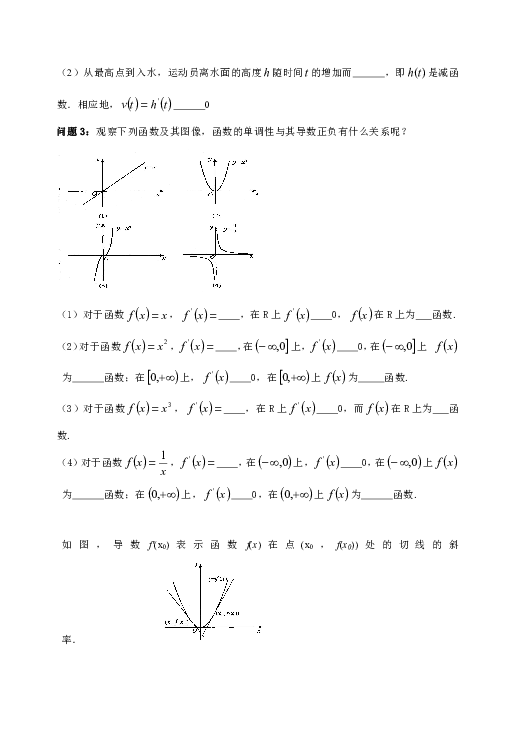
问题3:观察下列函数及其图像,函数的单调性与其导数正负有什么关系呢?
(1)对于函数, ,在R上 0,在R上为 函数.
(2)对于函数, ,在上, 0,在上 为 函数;在上, 0,在上为 函数.
(3)对于函数, ,在R上 0,而在R上为 函数.
(4)对于函数, ,在上, 0,在上为 函数;在上, 0,在上为 函数.
如图,导数f'(x0)表示函数f(x)在点(x0,f(x0))处的切线的斜率.
在x=x0处,f'(x0)>0,切线是“左下右上”式的,这时,函数f(x)在x0附近单调递增;
在x=x1处,f'(x1)<0,切线是“左上右下”式的,这时,函数f(x)在x1附近单调递减.
问题4:一般的,在某个区间内,如果, 则在区间内为 ;如果, 则在区间内为. .
问题5:如果在某个区间内恒有0,那么函数有什么特征?
注:1、若在某区间上有有限个点使,在其余的点恒有,则仍为增函数(减函数的情形完全类似);2、由推出为增函数,但反之不一定.如函数在上单调递增,但.
知识点二、用函数的导数研究函数的单调性.
例1.已知导函数f'(x)的下列信息:
当时10;当x=4,或x=1时,f'(x)=0.
试画出函数图像的大致形状.
例2、判断函数的单调性,并求出单调区间。
(1)f(x)=x3+3x; (2)f(x)=x2—2x+3;
(3) (4)f(x)=2x3+3x2—24x+1.
问:求解函数单调区间的步骤:_________________________________________________.
【当堂检测】
1、判断函数的单调性,并求出单调区间:
(1);(2);(3).
2、请尝试完成课本26页练习2.
1.3.1函数的单调性与导数(第1课时)
【学习目标】
理解函数单调性和导数的关系.
2、会利用导数判断函数的单调性.
【重点难点】
重点:函数的单调性和导数的关系.
难点:利用导数判断函数的单调性.
【知识回顾】
回顾函数单调性的定义.
2、利用定义判断的单调性.
【问题探究】
知识点一、函数单调性和导数的关系
问题1:如上图(1),它表示跳水运动中高度随时间变化的函数的图像,
图(2)表示高台跳水运动员的速度随时间变化的函数的图像 运动员从起跳到最高点,以及从最高点到入水这两段时间的运动状态有什么区别?
问题2:
(1)运动员从起点到最高点,离水面的高度随时间的增加而 ,即是增函数.相应地, 0
(2)从最高点到入水,运动员离水面的高度随时间的增加而 ,即是减函数.相应地, 0
问题3:观察下列函数及其图像,函数的单调性与其导数正负有什么关系呢?
(1)对于函数, ,在R上 0,在R上为 函数.
(2)对于函数, ,在上, 0,在上 为 函数;在上, 0,在上为 函数.
(3)对于函数, ,在R上 0,而在R上为 函数.
(4)对于函数, ,在上, 0,在上为 函数;在上, 0,在上为 函数.
如图,导数f'(x0)表示函数f(x)在点(x0,f(x0))处的切线的斜率.
在x=x0处,f'(x0)>0,切线是“左下右上”式的,这时,函数f(x)在x0附近单调递增;
在x=x1处,f'(x1)<0,切线是“左上右下”式的,这时,函数f(x)在x1附近单调递减.
问题4:一般的,在某个区间内,如果, 则在区间内为 ;如果, 则在区间内为. .
问题5:如果在某个区间内恒有0,那么函数有什么特征?
注:1、若在某区间上有有限个点使,在其余的点恒有,则仍为增函数(减函数的情形完全类似);2、由推出为增函数,但反之不一定.如函数在上单调递增,但.
知识点二、用函数的导数研究函数的单调性.
例1.已知导函数f'(x)的下列信息:
当时1
试画出函数图像的大致形状.
例2、判断函数的单调性,并求出单调区间。
(1)f(x)=x3+3x; (2)f(x)=x2—2x+3;
(3) (4)f(x)=2x3+3x2—24x+1.
问:求解函数单调区间的步骤:_________________________________________________.
【当堂检测】
1、判断函数的单调性,并求出单调区间:
(1);(2);(3).
2、请尝试完成课本26页练习2.
