人教版八年级数学下册 18.1.1 平行四边形的性质课件(共2课时)
文档属性
| 名称 | 人教版八年级数学下册 18.1.1 平行四边形的性质课件(共2课时) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-01 21:11:49 | ||
图片预览



文档简介
(共36张PPT)
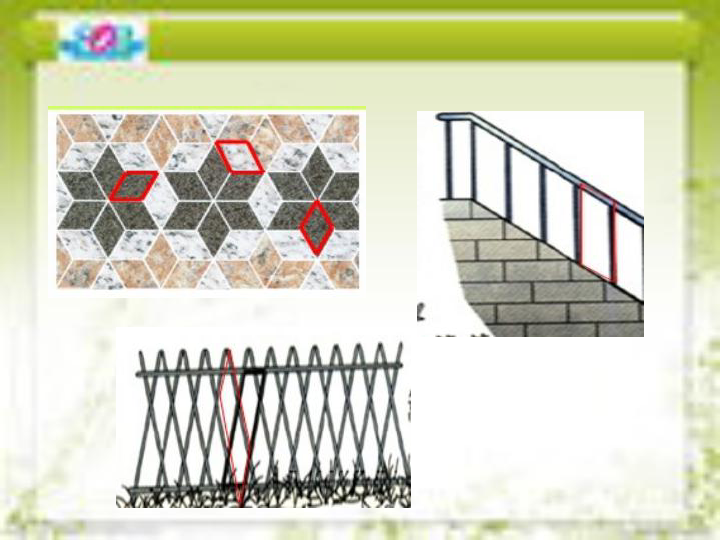
18.1 平行四边形
—— 平行四边形的性质(第1课时)
数学的天地里,重要的不是我们知道什么,而是我们怎么知道什么。
——毕达哥拉斯
观察与发现
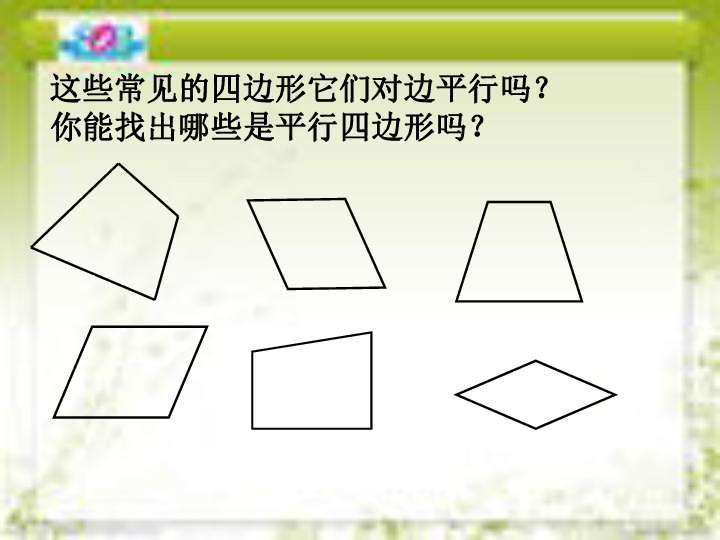
这些常见的四边形它们对边平行吗?
你能找出哪些是平行四边形吗?
四边形
两组对边分别平行的四边形叫做平行四边形.
定义
如图:四边形ABCD是平行四边形,
记作: ABCD
A
B
C
D
平行四边形的符号表示:
探索与发现
请你用你课前制作的平行四边形,进行观察与发现:
A
B
C
D
1.图中有哪些相等的角?
2.有哪些相等的边?
3.你能对你的猜想说明理由吗?
观察与猜想
A
B
C
D
1.相等的角有:
2.相等的边有:
∠A=∠C,∠B=∠D
AB=DC,AD=BC
验证结论
A
B
C
D
量一量:用直尺,量角器度量平行四边形的边和
角,得出AB=DC,AD=BC,∠A=∠C,∠B=∠D。
验证结论
剪一剪:把平行四边形沿着对角线剪开,叠合,得出两个完全重合的三角形。
小结:解决平行四边形的问题时,通常可以连结对角线转化为两个全等的三角形进行解题。
已知: ABCD
求证:AB=CD,BC=DA;
∠B=∠D,∠A=∠C.
A
B
C
D
即∠BAD=∠DCB
∵四边形ABCD是平行四边形
∴AB∥CD,AD∥BC
∴∠1=∠2,∠3=∠4
∠1=∠2
AC=CA
∠3=∠4
∴ △ABC≌△CDA(ASA)
∴AB=CD,BC=DA,
∠B=∠D
又∵∠1=∠2,∠3=∠4
∴∠1+∠4=∠2+∠3
在△ABC和△CDA中
证明:连接AC
2
1
3
4
验证结论
证一证
平行四边形的对边平行且相等.
平行四边形的对角相等.
平行四边形的性质
A
B
C
D
总结归纳
例题:如图,小明用一根36m长的绳子围成了一个平行四边形的场地,其中一条边AB长为8m.
⑵ 若∠A+∠C=200°,
则∠A和∠B分别为多少度?
解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC.
∵AB=8,
∴CD=8(m),
又AB+BC+CD+AD=36, ∴AD=BC=10(m).
⑴ 其他三条边各长多少?
解:∵四边形ABCD是平行四边形,
∴∠A=∠C,
∵∠A+∠C=200°
∴∠A=100°.
∵ AD∥BC
∴ ∠A+∠B=180°
∴ ∠B= 80°
A
D
B
C
应用举例
1.如图所示,四边形ABCD是平行四边形
1)若周长为30㎝,CD=6 ㎝,则AB= ㎝
BC= ㎝;AD= ㎝。
2)若∠A=70°,则∠B= 。
∠C= ∠D= .
3)若∠A+∠C=80°.则∠A= ;
∠D= 。
学以致用(定理的直接应用)
A
B
C
D
2.已知: ABCD,延长AB到E, 延长CD到F
使BE=DF
求证:AF=CE
学以致用(定理的综合应用)
3:在 ABCD中, ∠ABC 的平分线把对边分成4和3两部分,则这个平行四边形的周长是多少?
拓展与延伸(知识的综合应用)
如图:
通过探究,本节课你得到了哪些结论?
在探究平行四边形的性质过程中,你有哪些认识?
在运用平行四边形的性质解题时,你获得了什么思
想和方法?
感悟与收获
分层作业:
必做题:1.解决课前老师提出的问题。
2.教材习题18.1 1,2
选做题:(解决问题)农民李某想发展副业致 富,经考察地形后,在耕地旁边的荒地上开垦一平行四边形形状的鱼塘。能测得∠B=120° ,量得AD=50米,AB=80米。请你帮助李某计算一下鱼塘的对边AB、CD之间的距离及这个鱼塘的周长。
平行四边形的性质(2)
◆ 上节课我们掌握了平行四边形的哪些性质?
◆什么是平行四边形?
知识回顾
(1) 对边平行且相等.
对角相等.
对角线互相平分.
2.平行四边形的性质:
1.平行四边形的定义:
两组对边分别平行的四边形叫做平行四边形.
知识回顾
比 一 比
2、 的周长是20,已知AB=6,则
BC=__,CD=__.
1、判断正误:平行线间的线段相等. ( )
4
ABCD
6
3、 中,∠A比∠B大 30 ?, 则
∠A=__,∠D=__.
ABCD
4、若A、B、C三点不共线,则以这三点为
顶点的平行四边形有__个.
3
105°
75°
运用所学知识解决问题
E
F
H
G
A
B
D
C
运用所学知识解决问题
已知:如图,AB∥CD,EF∥GH.
请判断线段EF与GH有何数量关系?
讨 论
夹在两条平行线间的平行线段相等
A
B
C
D
O
上图的平行四边形ABCD中有几对全等三角形?
例1 如图:四边形ABCD是平行四边形,AB=10,AD=8,AC⊥BC,求BC、CD、AC、OA的长及 ABCD的面积。
A
D
B
C
O
学以致用
一位饱经沧桑的老人,经过一辈子的辛勤劳动,到晚年的时候,终于拥有了一块平行四边形的土地,由于年迈体弱,他决定把这块土地分给他的四个孩子,他是这样分的:
当四个孩子看到后,三个弟弟都抢着说应该把这四块地中最大的一块给对家里贡献最大的大哥,同学们,你认为他们能做到吗?为什么呢?
能力探究
A
C
D
B
o
●
M
ABCD的对角线AC与BD相交于O,直线EF过点 O与 AB 、CD分别相交于E 、F,试探究OE与OF的大小关系并说明理由。
A
B
C
D
O
E
F
●
●
●
1
2
3
4
探究一
●
O
D
C
B
A
E
F
●
O
D
C
B
A
E
F
(1)
(2)
在上述问题中,若直线EF绕与边DA、BC的延长线交于点E、F,(如图2),上述结论是否仍然成立?试说明理由。
变一变
●
●
●
●
在上述问题中,若将直线 EF绕点O旋转至下图(3)的位置时,上述结论是否仍然成立?
F
E
F
●
O
D
C
B
A
E
(1)
●
O
D
C
B
A
E
F
(3)
(3)
(4)
若此时再与两边延长线相交呢?
●
O
D
C
B
A
E
F
(4)
M
N
●
●
●
●
再变一变
小结:过平行四边形的对角线交点作直线与平行四边形的一组对边或对边的延长线相交,得到线段总相等。
AC=38mm,BC=24mm,OD=18mm,
求△OBC的周长.
C
B
A
O
D
X
有没有这样的平行四边形,
它的两条对角线长分别为14cm和20cm,
它的一边长为18cm?为什么?
例2 已知:如图,在 中,AC与BD相交于点O
ABCD
探究二
练习:5、如图, ABCD的对角线AC,BD相交于点O。已知AB=5cm,△AOB的周长和△BOC的周长相差3cm,则AD的长为__________
2cm或8cm
O
18.1 平行四边形
—— 平行四边形的性质(第1课时)
数学的天地里,重要的不是我们知道什么,而是我们怎么知道什么。
——毕达哥拉斯
观察与发现
这些常见的四边形它们对边平行吗?
你能找出哪些是平行四边形吗?
四边形
两组对边分别平行的四边形叫做平行四边形.
定义
如图:四边形ABCD是平行四边形,
记作: ABCD
A
B
C
D
平行四边形的符号表示:
探索与发现
请你用你课前制作的平行四边形,进行观察与发现:
A
B
C
D
1.图中有哪些相等的角?
2.有哪些相等的边?
3.你能对你的猜想说明理由吗?
观察与猜想
A
B
C
D
1.相等的角有:
2.相等的边有:
∠A=∠C,∠B=∠D
AB=DC,AD=BC
验证结论
A
B
C
D
量一量:用直尺,量角器度量平行四边形的边和
角,得出AB=DC,AD=BC,∠A=∠C,∠B=∠D。
验证结论
剪一剪:把平行四边形沿着对角线剪开,叠合,得出两个完全重合的三角形。
小结:解决平行四边形的问题时,通常可以连结对角线转化为两个全等的三角形进行解题。
已知: ABCD
求证:AB=CD,BC=DA;
∠B=∠D,∠A=∠C.
A
B
C
D
即∠BAD=∠DCB
∵四边形ABCD是平行四边形
∴AB∥CD,AD∥BC
∴∠1=∠2,∠3=∠4
∠1=∠2
AC=CA
∠3=∠4
∴ △ABC≌△CDA(ASA)
∴AB=CD,BC=DA,
∠B=∠D
又∵∠1=∠2,∠3=∠4
∴∠1+∠4=∠2+∠3
在△ABC和△CDA中
证明:连接AC
2
1
3
4
验证结论
证一证
平行四边形的对边平行且相等.
平行四边形的对角相等.
平行四边形的性质
A
B
C
D
总结归纳
例题:如图,小明用一根36m长的绳子围成了一个平行四边形的场地,其中一条边AB长为8m.
⑵ 若∠A+∠C=200°,
则∠A和∠B分别为多少度?
解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC.
∵AB=8,
∴CD=8(m),
又AB+BC+CD+AD=36, ∴AD=BC=10(m).
⑴ 其他三条边各长多少?
解:∵四边形ABCD是平行四边形,
∴∠A=∠C,
∵∠A+∠C=200°
∴∠A=100°.
∵ AD∥BC
∴ ∠A+∠B=180°
∴ ∠B= 80°
A
D
B
C
应用举例
1.如图所示,四边形ABCD是平行四边形
1)若周长为30㎝,CD=6 ㎝,则AB= ㎝
BC= ㎝;AD= ㎝。
2)若∠A=70°,则∠B= 。
∠C= ∠D= .
3)若∠A+∠C=80°.则∠A= ;
∠D= 。
学以致用(定理的直接应用)
A
B
C
D
2.已知: ABCD,延长AB到E, 延长CD到F
使BE=DF
求证:AF=CE
学以致用(定理的综合应用)
3:在 ABCD中, ∠ABC 的平分线把对边分成4和3两部分,则这个平行四边形的周长是多少?
拓展与延伸(知识的综合应用)
如图:
通过探究,本节课你得到了哪些结论?
在探究平行四边形的性质过程中,你有哪些认识?
在运用平行四边形的性质解题时,你获得了什么思
想和方法?
感悟与收获
分层作业:
必做题:1.解决课前老师提出的问题。
2.教材习题18.1 1,2
选做题:(解决问题)农民李某想发展副业致 富,经考察地形后,在耕地旁边的荒地上开垦一平行四边形形状的鱼塘。能测得∠B=120° ,量得AD=50米,AB=80米。请你帮助李某计算一下鱼塘的对边AB、CD之间的距离及这个鱼塘的周长。
平行四边形的性质(2)
◆ 上节课我们掌握了平行四边形的哪些性质?
◆什么是平行四边形?
知识回顾
(1) 对边平行且相等.
对角相等.
对角线互相平分.
2.平行四边形的性质:
1.平行四边形的定义:
两组对边分别平行的四边形叫做平行四边形.
知识回顾
比 一 比
2、 的周长是20,已知AB=6,则
BC=__,CD=__.
1、判断正误:平行线间的线段相等. ( )
4
ABCD
6
3、 中,∠A比∠B大 30 ?, 则
∠A=__,∠D=__.
ABCD
4、若A、B、C三点不共线,则以这三点为
顶点的平行四边形有__个.
3
105°
75°
运用所学知识解决问题
E
F
H
G
A
B
D
C
运用所学知识解决问题
已知:如图,AB∥CD,EF∥GH.
请判断线段EF与GH有何数量关系?
讨 论
夹在两条平行线间的平行线段相等
A
B
C
D
O
上图的平行四边形ABCD中有几对全等三角形?
例1 如图:四边形ABCD是平行四边形,AB=10,AD=8,AC⊥BC,求BC、CD、AC、OA的长及 ABCD的面积。
A
D
B
C
O
学以致用
一位饱经沧桑的老人,经过一辈子的辛勤劳动,到晚年的时候,终于拥有了一块平行四边形的土地,由于年迈体弱,他决定把这块土地分给他的四个孩子,他是这样分的:
当四个孩子看到后,三个弟弟都抢着说应该把这四块地中最大的一块给对家里贡献最大的大哥,同学们,你认为他们能做到吗?为什么呢?
能力探究
A
C
D
B
o
●
M
ABCD的对角线AC与BD相交于O,直线EF过点 O与 AB 、CD分别相交于E 、F,试探究OE与OF的大小关系并说明理由。
A
B
C
D
O
E
F
●
●
●
1
2
3
4
探究一
●
O
D
C
B
A
E
F
●
O
D
C
B
A
E
F
(1)
(2)
在上述问题中,若直线EF绕与边DA、BC的延长线交于点E、F,(如图2),上述结论是否仍然成立?试说明理由。
变一变
●
●
●
●
在上述问题中,若将直线 EF绕点O旋转至下图(3)的位置时,上述结论是否仍然成立?
F
E
F
●
O
D
C
B
A
E
(1)
●
O
D
C
B
A
E
F
(3)
(3)
(4)
若此时再与两边延长线相交呢?
●
O
D
C
B
A
E
F
(4)
M
N
●
●
●
●
再变一变
小结:过平行四边形的对角线交点作直线与平行四边形的一组对边或对边的延长线相交,得到线段总相等。
AC=38mm,BC=24mm,OD=18mm,
求△OBC的周长.
C
B
A
O
D
X
有没有这样的平行四边形,
它的两条对角线长分别为14cm和20cm,
它的一边长为18cm?为什么?
例2 已知:如图,在 中,AC与BD相交于点O
ABCD
探究二
练习:5、如图, ABCD的对角线AC,BD相交于点O。已知AB=5cm,△AOB的周长和△BOC的周长相差3cm,则AD的长为__________
2cm或8cm
O
