六年级下册数学课件-负数-人教版(共24张PPT)
文档属性
| 名称 | 六年级下册数学课件-负数-人教版(共24张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 750.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-01 10:18:10 | ||
图片预览







文档简介
(共24张PPT)
负 数
濮阳县第二实验小学
请说出和老师相反的词语和句子
欣欣超市今天盈利2000元
我在银行存入300元
电梯上升了15层
上车15人
认真阅读课本2~4页。画出自己认为重要的知识,并标出来自己不能读懂的知识。
(1)你是怎样理解“两种相反意义的量” 的?请举例说明。
(2)+2还能用什么来表示,为什么能省略正号,负号呢?
(3)0是负数,还是正数?
思考并回答下面的问题
正数
负数
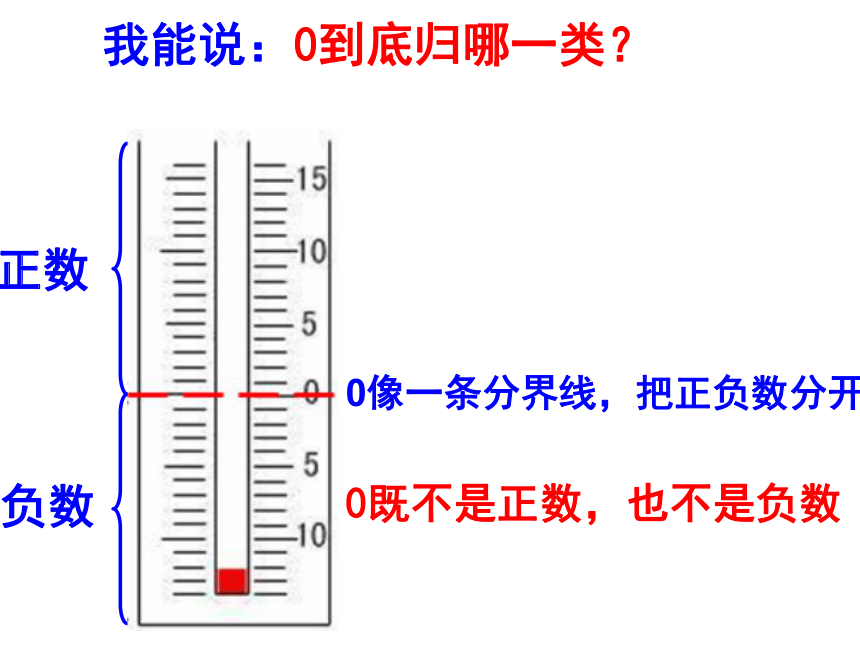
我能说:0到底归哪一类?
0像一条分界线,把正负数分开
0既不是正数,也不是负数
用预习到的新知识来表示刚才句子中的量:
(1)欣欣超市今天盈利2000元
欣欣超市今天 亏损2000元
(2)河水水位上涨10毫米
河水水位下降10毫米
(3)电梯上升7层 电梯下降7层
(4)上车15人 下车15人
(5)转来4名同学 转走4名同学
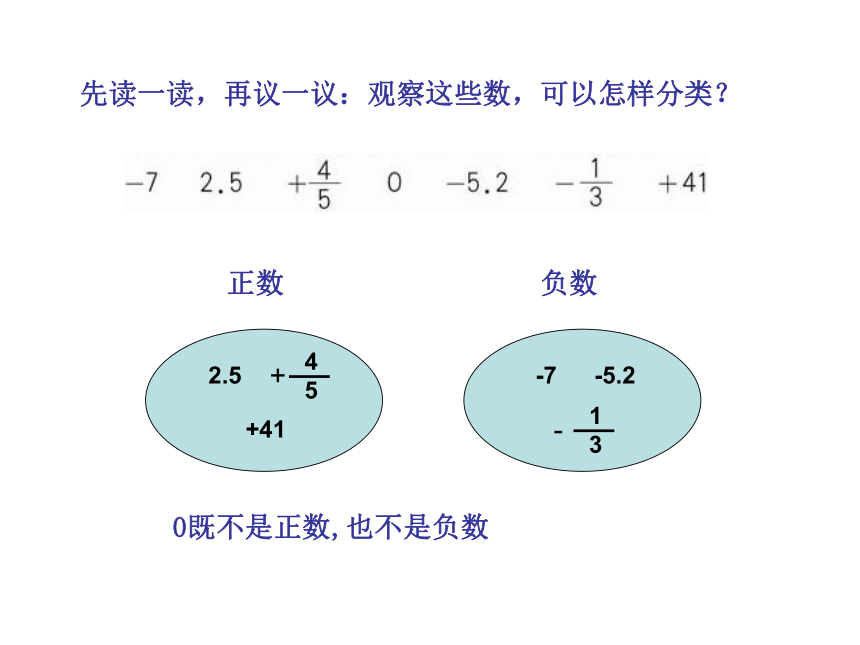
先读一读,再议一议:观察这些数,可以怎样分类?
正数
负数
-7
2.5
+41
-5.2
0既不是正数,也不是负数
我能辩
1、任何一个负数都比正数小。( )
2、一个数不是正数就是负数。( )
3、因为“4”前面没有“+”号,所以“4”不是正数。( )
4、上车5人记作“+5人”,则下车4人记作“-4人”。( )
5、正数都比0大,负数都比0小。( )
6、5゜C和+5゜C所表示的气温一样高。( )
√
√
√
√
×
×
珠穆朗玛峰大约比海平面高8844.43米,吐鲁番盆地大约比海平面低155米。
海平面
珠穆朗玛峰
吐鲁番盆地
高度看作0.
把海平面高度看作( ),
比海平面高的用( )表示,
比海平面低的用( )表示。
0
+几或几
-几
生活中什么时候还需要用到负数?
生活万花筒
电梯
海平面
行走
体育课
濮阳温度
包装袋
月球
1
电梯中的学问
一幢大楼高18层,地面以下有2层,地面以上第三层记作+3层,地面以下第一层记作什么?地面以下第二层记作什么?
把海平面的高度记作0米,我国最大的咸水湖——青海湖,它高于海平面3193米,世界上最深的咸水湖——死海,低于海平面392米,你会用正负数表示青海湖和死海的海拔高度吗?
用正负数表示下面各地的海拔高度
行走中的正负数
如果从某点向北的距离用正数表示,那么+350米表示什么?—200米表示什么?
体育课中的正负数
在一次体育测试中,老师对8名同学进行了仰卧起坐的测试,以38个为标准,超过的用正数表示,不足的用负数表示,这8名同学的成绩分别是2,—3,4,—1, 0, 1, —5,0.
这八名同学实际各做了多少个仰卧起坐?
2019年12月4日,濮阳气温-5℃~2℃,这天濮阳的温差是多少?
包装袋上的学问
一种饼干包装袋上标着:净重(150±5克),你能解释它的含义吗?
月球上的正负数
月球表面白天的平均温度是零上123℃,记作( ),夜间的平均温度是零下150℃,记作( )
通过今天的学习, 你知道了关于负数的什么知识?你用什么方法学习的?
畅所欲言
你还想了解有关负数的什么知识?
中国是最早认识和使用负数的国家。据说在2000多年前的《九章算术》记载,那时的人就有了“粮食入仓为正,出仓为负 ;收入的钱为正,付出的钱为负”的思想。
1700多年前,我国数学家刘徽在注解《九章算术》时,更明确地提出了正数和负数的概念。他在筹算中规定“正算赤,负算黑”,就是用红色算筹表示正数,黑色算筹表示负数.这个记载,比国外早了七八百年。
用不同颜色的数表示正负数的习惯,一直保留在现在。现在一般 红色表示负数,报纸上登载某国经济上出现赤字,表示支出大于收入,财政上亏了钱。
1700多年前,汉朝数学家刘徽除了用两种不同颜色来区分外,还用摆放位置的正与斜来区分。
由于记录时换色不方便,到了十三世纪,开始用画斜杠的方法来表示,还用加符号的方法来表示。
国外对负数的认识经历了一个曲折的过程,并且出现了各种负数的形式。直到20世纪初,法国数学家吉拉尔首次用“+”和“-”来表示,一直沿用至今。
负数在其他国家的坎坷历程:
与中国古代数学家不同,西方数学家更多的是研究负数存在的合理性。欧洲14世纪最有成就的法国数学家丘凯把负数说成是荒谬的数 ,到了16世纪和17世纪,欧洲大部分的数学家还不承认负数是数 。帕斯卡认为0减去4是纯粹的胡说 。帕斯卡的朋友安润德提出一个有趣的说法来反对负数,他认为(—1):1=1:(—1),那么较小的数与较大的数的比怎么能等于较大的数与较小的数的比呢?直到1712年,连莱布尼兹也承认这种说法合理。英国数学家瓦里承认负数,同时认为负数小于零而大于无穷大(1655年)。
英国著名数学家德·摩根在1831年时仍认为负数是虚构的。他用以下的例子说明这一点:父亲56岁,儿子29岁,何时父亲的年龄是儿子的2倍?他列方程56+x=2(29+x),并解得x=—2,他称此解是荒唐的。当然,到了18世纪,欧洲排斥负数的人 已经不多了。
随着19世纪整数论基础的建立,负数在逻辑的合理性才真正确立。
恳请专家指导
负 数
濮阳县第二实验小学
请说出和老师相反的词语和句子
欣欣超市今天盈利2000元
我在银行存入300元
电梯上升了15层
上车15人
认真阅读课本2~4页。画出自己认为重要的知识,并标出来自己不能读懂的知识。
(1)你是怎样理解“两种相反意义的量” 的?请举例说明。
(2)+2还能用什么来表示,为什么能省略正号,负号呢?
(3)0是负数,还是正数?
思考并回答下面的问题
正数
负数
我能说:0到底归哪一类?
0像一条分界线,把正负数分开
0既不是正数,也不是负数
用预习到的新知识来表示刚才句子中的量:
(1)欣欣超市今天盈利2000元
欣欣超市今天 亏损2000元
(2)河水水位上涨10毫米
河水水位下降10毫米
(3)电梯上升7层 电梯下降7层
(4)上车15人 下车15人
(5)转来4名同学 转走4名同学
先读一读,再议一议:观察这些数,可以怎样分类?
正数
负数
-7
2.5
+41
-5.2
0既不是正数,也不是负数
我能辩
1、任何一个负数都比正数小。( )
2、一个数不是正数就是负数。( )
3、因为“4”前面没有“+”号,所以“4”不是正数。( )
4、上车5人记作“+5人”,则下车4人记作“-4人”。( )
5、正数都比0大,负数都比0小。( )
6、5゜C和+5゜C所表示的气温一样高。( )
√
√
√
√
×
×
珠穆朗玛峰大约比海平面高8844.43米,吐鲁番盆地大约比海平面低155米。
海平面
珠穆朗玛峰
吐鲁番盆地
高度看作0.
把海平面高度看作( ),
比海平面高的用( )表示,
比海平面低的用( )表示。
0
+几或几
-几
生活中什么时候还需要用到负数?
生活万花筒
电梯
海平面
行走
体育课
濮阳温度
包装袋
月球
1
电梯中的学问
一幢大楼高18层,地面以下有2层,地面以上第三层记作+3层,地面以下第一层记作什么?地面以下第二层记作什么?
把海平面的高度记作0米,我国最大的咸水湖——青海湖,它高于海平面3193米,世界上最深的咸水湖——死海,低于海平面392米,你会用正负数表示青海湖和死海的海拔高度吗?
用正负数表示下面各地的海拔高度
行走中的正负数
如果从某点向北的距离用正数表示,那么+350米表示什么?—200米表示什么?
体育课中的正负数
在一次体育测试中,老师对8名同学进行了仰卧起坐的测试,以38个为标准,超过的用正数表示,不足的用负数表示,这8名同学的成绩分别是2,—3,4,—1, 0, 1, —5,0.
这八名同学实际各做了多少个仰卧起坐?
2019年12月4日,濮阳气温-5℃~2℃,这天濮阳的温差是多少?
包装袋上的学问
一种饼干包装袋上标着:净重(150±5克),你能解释它的含义吗?
月球上的正负数
月球表面白天的平均温度是零上123℃,记作( ),夜间的平均温度是零下150℃,记作( )
通过今天的学习, 你知道了关于负数的什么知识?你用什么方法学习的?
畅所欲言
你还想了解有关负数的什么知识?
中国是最早认识和使用负数的国家。据说在2000多年前的《九章算术》记载,那时的人就有了“粮食入仓为正,出仓为负 ;收入的钱为正,付出的钱为负”的思想。
1700多年前,我国数学家刘徽在注解《九章算术》时,更明确地提出了正数和负数的概念。他在筹算中规定“正算赤,负算黑”,就是用红色算筹表示正数,黑色算筹表示负数.这个记载,比国外早了七八百年。
用不同颜色的数表示正负数的习惯,一直保留在现在。现在一般 红色表示负数,报纸上登载某国经济上出现赤字,表示支出大于收入,财政上亏了钱。
1700多年前,汉朝数学家刘徽除了用两种不同颜色来区分外,还用摆放位置的正与斜来区分。
由于记录时换色不方便,到了十三世纪,开始用画斜杠的方法来表示,还用加符号的方法来表示。
国外对负数的认识经历了一个曲折的过程,并且出现了各种负数的形式。直到20世纪初,法国数学家吉拉尔首次用“+”和“-”来表示,一直沿用至今。
负数在其他国家的坎坷历程:
与中国古代数学家不同,西方数学家更多的是研究负数存在的合理性。欧洲14世纪最有成就的法国数学家丘凯把负数说成是荒谬的数 ,到了16世纪和17世纪,欧洲大部分的数学家还不承认负数是数 。帕斯卡认为0减去4是纯粹的胡说 。帕斯卡的朋友安润德提出一个有趣的说法来反对负数,他认为(—1):1=1:(—1),那么较小的数与较大的数的比怎么能等于较大的数与较小的数的比呢?直到1712年,连莱布尼兹也承认这种说法合理。英国数学家瓦里承认负数,同时认为负数小于零而大于无穷大(1655年)。
英国著名数学家德·摩根在1831年时仍认为负数是虚构的。他用以下的例子说明这一点:父亲56岁,儿子29岁,何时父亲的年龄是儿子的2倍?他列方程56+x=2(29+x),并解得x=—2,他称此解是荒唐的。当然,到了18世纪,欧洲排斥负数的人 已经不多了。
随着19世纪整数论基础的建立,负数在逻辑的合理性才真正确立。
恳请专家指导
