六年级下册数学课件-圆柱的表面积-人教版(共39张PPT)
文档属性
| 名称 | 六年级下册数学课件-圆柱的表面积-人教版(共39张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 31.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-01 10:28:04 | ||
图片预览







文档简介
(共39张PPT)
城关三小
一、导入新课,点明课题
二、自主探究,合作交流
借助学具思考以下问题:
1、圆柱的表面积包括哪几部分的面积? 2、怎样计算圆柱的表面积?
3、圆柱的侧面积怎样计算?为什么能这样计算?
4、圆柱的表面积计算公式是什么?
三、展示汇报,共同提高
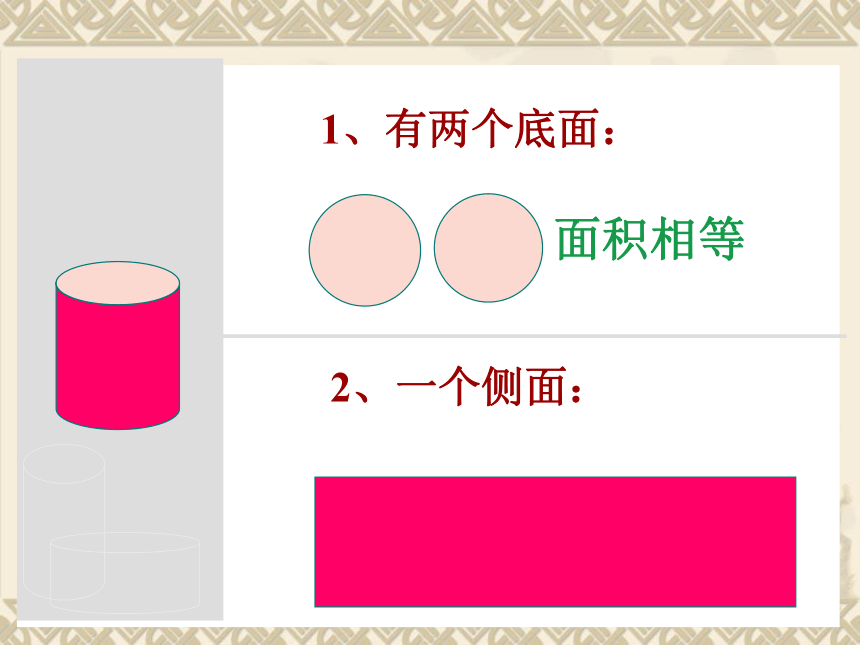
1、有两个底面:
2、一个侧面:
面积相等
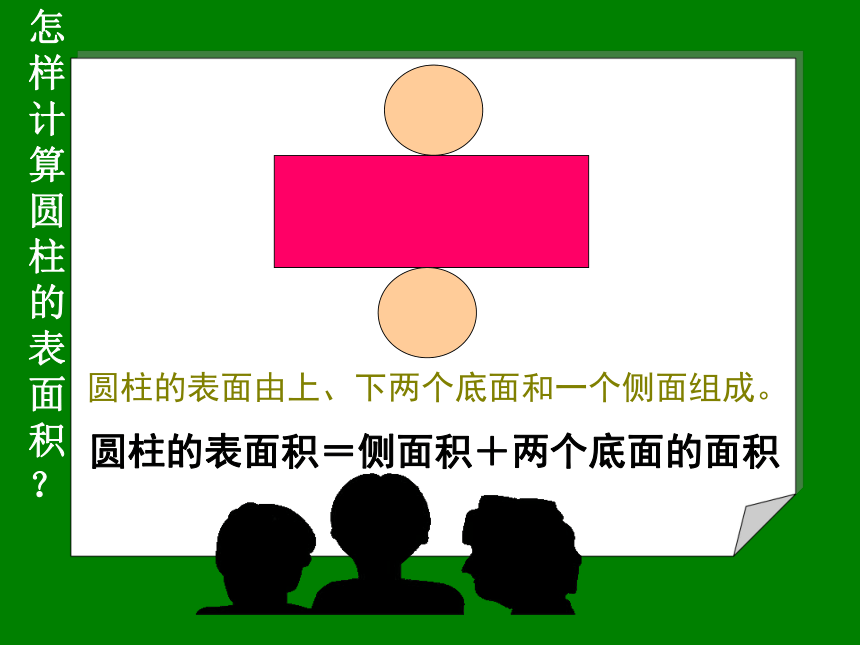
怎样计算圆柱的表面积?
圆柱的表面由上、下两个底面和一个侧面组成。
圆柱的表面积=侧面积+两个底面的面积
怎样计算圆柱的表面积 ?
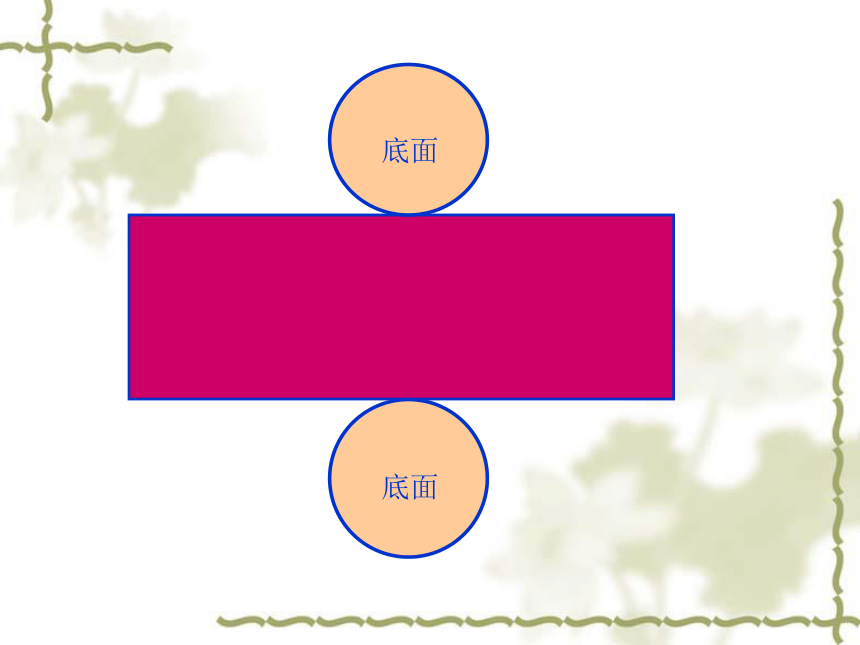
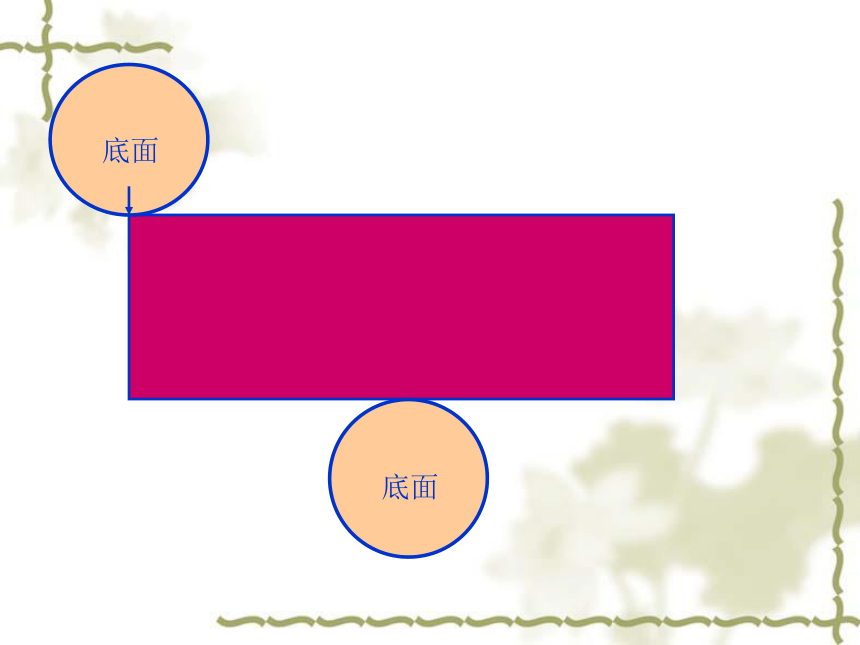
圆柱的侧面积怎样计算?为什么能这样计算?
底面
底面
底面
底面
底面
底面
底面
底面
底面
底面
底面
底面
底面
底面
底面
底面
底面
底面
高
底面
长方形的长等于圆柱底面的周长,宽等于圆柱的高。
你会求侧面的面积吗?
长方形的面积 = 长 × 宽
圆柱的侧面积 = 底面周长 ×高
S侧= Ch
圆柱的表面积计算公式
S表=2 πrh+2 πr2
S表= π dh+2 π(d/2)2
S表= Ch+2 π(C/2 π )2
侧面积:2×3.14×5×10=314(cm?)
底面积:3.14×5?=78.5(cm?)
表面积:314+78.5×2=471 (cm?)
答:制作一个至少需要471平方厘米的铁皮。
例 1
一顶圆柱形厨师帽,高28cm,帽顶直径20cm,做这样一顶帽需要用多少面料?(得数保留整十平方厘米)
侧面积:3.14×20×28=1758.4(cm?)
底面积:3.14×(20÷2)?=314 (cm?)
面料:1758.4+314=2072.4≈2080 (cm?)
答:做一顶帽子需要用2080 cm?的面料。
关于圆柱你还有那些不明白的地方?学了本节课你又产生了哪些新的疑问?
四、回顾整理,总结归纳
通过本节课的学习,你有什么收获?
五、巩固应用,内化提高
提出一个问题比解决一个问题更能体
现创造性的思维!你能编一道题吗?
我当小老师:
小明有一个圆柱形水壶,高20厘米,底面半径5厘米 。妈妈给小明的水壶做了一个布套, 至少用了多少布料?
想:题中给的已知条件有哪些?所求问题是什么?求用的布料就是求什么?
(1) 侧面积:2X3.14X5X20=628(平方厘米)
(2) 底面积:3.14X5? =78.5(平方厘米)
(3)表面积: 628+78.5X2=785(平方厘米)
做一个无盖的圆柱形铁皮水桶,高是5分米。底面直径4分米,至少需要多大面积的铁皮?
水桶没有盖,说明它只有一个底面。
(1)水桶的侧面积:
3.14 ×4 ×5=62.8(平方分米)
(2)水桶的底面积:
3.14 ×(4÷2) 2=12.56(平方分米)
(3)需要铁皮:
62.8+12.56=75.36(平方分米)
挑战自我
一个圆柱的侧面展开是个边长为9.42cm的正方形,这个圆柱的表面积是多少平方厘米?(只列式不计算)
9.42×9.42+3.14×(9.42÷3.14÷2)?×2
城关三小
一、导入新课,点明课题
二、自主探究,合作交流
借助学具思考以下问题:
1、圆柱的表面积包括哪几部分的面积? 2、怎样计算圆柱的表面积?
3、圆柱的侧面积怎样计算?为什么能这样计算?
4、圆柱的表面积计算公式是什么?
三、展示汇报,共同提高
1、有两个底面:
2、一个侧面:
面积相等
怎样计算圆柱的表面积?
圆柱的表面由上、下两个底面和一个侧面组成。
圆柱的表面积=侧面积+两个底面的面积
怎样计算圆柱的表面积 ?
圆柱的侧面积怎样计算?为什么能这样计算?
底面
底面
底面
底面
底面
底面
底面
底面
底面
底面
底面
底面
底面
底面
底面
底面
底面
底面
高
底面
长方形的长等于圆柱底面的周长,宽等于圆柱的高。
你会求侧面的面积吗?
长方形的面积 = 长 × 宽
圆柱的侧面积 = 底面周长 ×高
S侧= Ch
圆柱的表面积计算公式
S表=2 πrh+2 πr2
S表= π dh+2 π(d/2)2
S表= Ch+2 π(C/2 π )2
侧面积:2×3.14×5×10=314(cm?)
底面积:3.14×5?=78.5(cm?)
表面积:314+78.5×2=471 (cm?)
答:制作一个至少需要471平方厘米的铁皮。
例 1
一顶圆柱形厨师帽,高28cm,帽顶直径20cm,做这样一顶帽需要用多少面料?(得数保留整十平方厘米)
侧面积:3.14×20×28=1758.4(cm?)
底面积:3.14×(20÷2)?=314 (cm?)
面料:1758.4+314=2072.4≈2080 (cm?)
答:做一顶帽子需要用2080 cm?的面料。
关于圆柱你还有那些不明白的地方?学了本节课你又产生了哪些新的疑问?
四、回顾整理,总结归纳
通过本节课的学习,你有什么收获?
五、巩固应用,内化提高
提出一个问题比解决一个问题更能体
现创造性的思维!你能编一道题吗?
我当小老师:
小明有一个圆柱形水壶,高20厘米,底面半径5厘米 。妈妈给小明的水壶做了一个布套, 至少用了多少布料?
想:题中给的已知条件有哪些?所求问题是什么?求用的布料就是求什么?
(1) 侧面积:2X3.14X5X20=628(平方厘米)
(2) 底面积:3.14X5? =78.5(平方厘米)
(3)表面积: 628+78.5X2=785(平方厘米)
做一个无盖的圆柱形铁皮水桶,高是5分米。底面直径4分米,至少需要多大面积的铁皮?
水桶没有盖,说明它只有一个底面。
(1)水桶的侧面积:
3.14 ×4 ×5=62.8(平方分米)
(2)水桶的底面积:
3.14 ×(4÷2) 2=12.56(平方分米)
(3)需要铁皮:
62.8+12.56=75.36(平方分米)
挑战自我
一个圆柱的侧面展开是个边长为9.42cm的正方形,这个圆柱的表面积是多少平方厘米?(只列式不计算)
9.42×9.42+3.14×(9.42÷3.14÷2)?×2
