(新教材)2019—2020(浙江)人教版物理必修第二册同步学案讲义:第八章【拓展】动能定理的综合应用含答案
文档属性
| 名称 | (新教材)2019—2020(浙江)人教版物理必修第二册同步学案讲义:第八章【拓展】动能定理的综合应用含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 712.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-03-01 11:22:23 | ||
图片预览




文档简介
第 14 页 共 14 页
(新教材)2019—2020(浙江)人教版物理必修第二册同步学案讲义:第八章【拓展】动能定理的综合应用含答案
拓展:动能定理的综合应用
拓展点一 动能定理与牛顿运动定律的比较
1.理解比较
比较 牛顿第二定律 动能定理
作用 合外力与加速度的关系 合外力做的功与动能变化量的关系
公式 F=ma W=Ek2-Ek1
研究力和运动的关系 力的瞬间作用效果 力对空间的积累效果
运动过程中细节的考虑 考虑 不考虑
作用力 恒力 恒力或变力
2.应用比较
比较 牛顿运动定律 动能定理
相同点 确定研究对象,对物体进行受力分析和运动过程分析
适用条件 只能研究恒力作用下物体的运动的情况 对于物体在恒力或变力的作用下,物体做直线运动或曲线运动均适用
应用方法 要考虑运动过程的每一个细节,结合运动学公式 只考虑各力的做功情况及初、末状态的动能
运算方法 矢量运算 代数运算
[试题案例]
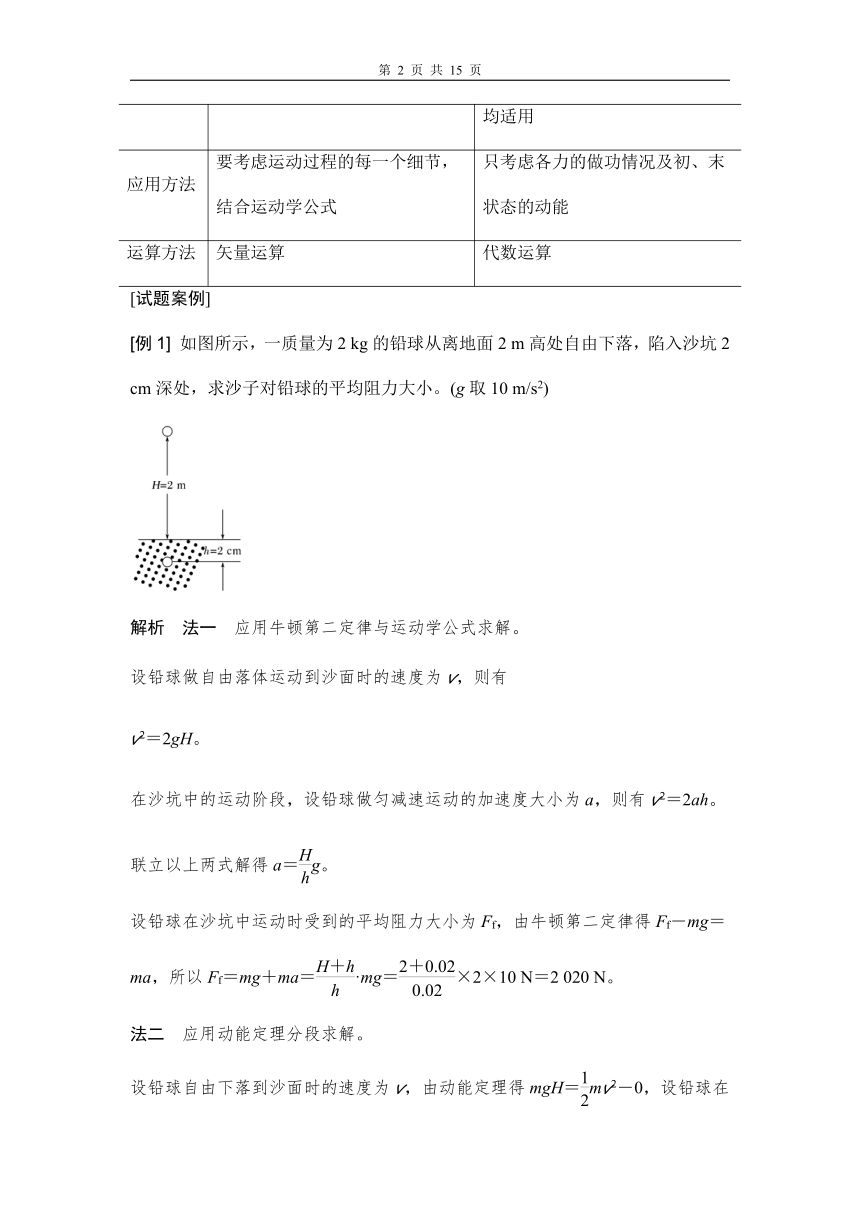
[例1] 如图所示,一质量为2 kg的铅球从离地面2 m高处自由下落,陷入沙坑2 cm深处,求沙子对铅球的平均阻力大小。(g取10 m/s2)
解析 法一 应用牛顿第二定律与运动学公式求解。
设铅球做自由落体运动到沙面时的速度为v,则有
v2=2gH。
在沙坑中的运动阶段,设铅球做匀减速运动的加速度大小为a,则有v2=2ah。
联立以上两式解得a=g。
设铅球在沙坑中运动时受到的平均阻力大小为Ff,由牛顿第二定律得Ff-mg=ma,所以Ff=mg+ma=·mg=×2×10 N=2 020 N。
法二 应用动能定理分段求解。
设铅球自由下落到沙面时的速度为v,由动能定理得mgH=mv2-0,设铅球在沙中受到的平均阻力大小为Ff,由动能定理得mgh-Ffh=0-mv2,联立以上两式得Ff=mg=2 020 N。
法三 应用动能定理全程求解。
铅球下落全过程都受重力,只有进入沙中铅球才受阻力Ff,重力做功WG=mg(H+h),阻力做功Wf=-Ffh。由动能定理得mg(H+h)-Ffh=0-0,代入数据得Ff=2 020 N。
答案 2 020 N
[针对训练1] 如图是冰上体育比赛“冰壶运动”的场地示意图(冰面水平)。在某次训练中,甲队员将质量m=20 kg的一个冰壶从左侧的A处向右推出,冰壶沿中心线运动到与A点相距为x=30 m的营垒中心O处恰好停下。此后,乙队员将完全相同的第二个冰壶同样在A处向右推出,冰壶从A处运动到O处经过的时间为t=10 s。已知两个冰壶与冰面间的动摩擦因数都为μ=0.02,冰壶都可视为质点,取g=10 m/s2。求:
(1)第一个冰壶被推出时的动能;
(2)第二个冰壶即将碰到第一个冰壶时的速度大小。
解析 (1)法一 牛顿第二定律
根据牛顿第二定律Ff=μmg=ma
根据运动学公式得v2=2ax=2μgx
动能的表达式Ek=mv2
联立并代入题给数据得Ek=μmgx=0.02×20×10×30 J=120 J。
法二 动能定理
对于甲队员推出的冰壶,由动能定理可得-μmgx=0-Ek1,代入数据得Ek1=120 J,故第一个冰壶被推出时的动能为120 J。
(2)第二个冰壶从A处运动到O处做匀减速运动,有μmg=ma,设冰壶在时间t内初、末速度分别为v2、v2′,则有v2′=v2-at,位移关系x=v2t-at2,代入数据解得第二个冰壶即将碰到第一个冰壶时的速度为v2′=2 m/s。
答案 (1)120 J (2)2 m/s
拓展点二 动能定理与图像的结合
分析动能定理和图像结合的问题时一定要弄清图像的物理意义,要特别注意图像的形状、交点、截距、斜率、面积等信息,并结合运动图像构建相应的物理模型,选择合理的规律求解有关问题。
[试题案例]
[例2] 如图甲所示,在水平地面上放置一个质量为m=4 kg的物体,让其在随位移均匀减小的水平推力作用下运动,推力F随位移x变化的图像如图乙所示,已
F与位移关系图线围成的面积表示功。
知物体与地面之间的动摩擦因数为μ=0.5,g取10 m/s2,求:
(1)出发时物体运动的加速度大小;
(2)物体能够运动的最大位移。
解析 (1)由牛顿第二定律得F-μmg=ma,
当推力F0=100 N时,物体所受的合力最大,加速度最大,代入数据得a=20 m/s2。
(2)根据图像得推力对物体做的功等于图线与x轴围成的面积,则推力对物体做功
W=F0x0=250 J,
根据动能定理可得W-μmgxm=0,
解得xm=12.5 m。
答案 (1)20 m/s2 (2)12.5 m
方法总结 “三步法”分析动能定理结合图像问题
[针对训练2] (多选)在平直公路上,汽车由静止开始做匀加速运动,当速度达到vm后立即关闭发动机直到停止,v-t图像如图所示。设汽车的牵引力为F,摩擦力为Ff,全过程中牵引力做功W1,克服摩擦力做功W2,则( )
A.F∶Ff=1∶3 B.F∶Ff=4∶1
C.W1∶W2=1∶1 D.W1∶W2=1∶3
解析 全过程初、末状态的动能都为零,
对全过程应用动能定理得W1-W2=0①
即W1=W2,选项C正确;
设物体在0~1 s内和1~4 s内运动的位移大小分别为s1、s2,则W1=Fs1②
W2=Ff(s1+s2)③
在v-t图像中,图像与时间轴包围的面积表示位移,由图像可知,s2=3s1④
由②③④式解得F∶Ff=4∶1,选项B正确。
答案 BC
拓展点三 利用动能定理处理曲线运动的多过程问题
1.平抛运动、圆周运动属于曲线运动,若只涉及位移和速度而不涉及时间,应优先考虑用动能定理列式求解。
2.用动能定理解题,关键是对研究对象进行准确的受力分析及运动过程分析,并画出物体运动过程的草图,让草图帮助我们理解物理过程和各量关系。
3.若物体的运动过程包含多个运动阶段,可分段应用动能定理,也可全程运用动能定理。若不涉及中间量,全程应用动能定理更简单、更方便。若涉及多个力做功,应注意力与位移的对应性。
[试题案例]
[例3] 如图所示,半径r1= m的圆弧轨道AB与水平轨道BC相切于B点,CD为r2=0.40 m的半圆轨道,另一半径R=1.00 m的圆弧轨道EF与CD靠近,E点略低于D点。一质量m=1 kg的小物块(可视为质点)从A点以初速度v0=2 m/s沿轨道下滑,在AB段运动过程中始终受到竖直向上的F=10 N的力作用,进入BC段后撤去。已知AB高度为h,BC长L=1.00 m,小物块与BC间动摩擦因数μ=0.2,其余光滑,EF轨道对应的圆心角θ=60°,所有轨道均固定在同一竖直平面内,不考虑小物块在各轨道相接处的速度大小的变化,忽略空气阻力,g取
10 m/s2。求:
(1)当小物块沿圆弧轨道AB运动到B点时,轨道对小物块的作用力大小;
(2)若小物块在B点的速度为5 m/s,且在刚进入BC段时撤去力F,请通过计算判断小物块能否通过D点;
(3)小物块能进入EF轨道,且不越过F点,小物块在D点的速度范围。
【审题指导】
题干关键点 提取信息
竖直向上的F=10 N的力 在AB段物块有恒力和重力做功
进入BC段后撤去F 在BC段物块只有摩擦力做功
物块能否通过D点 物块恰好过D点的条件是重力提供向心力
进入EF轨道,不越过F点 进入EF的最小速度对应过D点的最小速度,进入EF的最大速度对应到F点时速度为零
解析 (1)小物块从A到B,由动能定理得
mgh-Fh=mv-mv,解得vB=2 m/s。
在B点,由牛顿第二定律得F+FN-mg=meq \f(v,r1),
解得FN=5 N。
(2)假设小物块能从B到D,由动能定理得-2mgr2-μmgL=mv-mvB′2,解得vD= m/s。
若小物块恰好过D点,则mg=,解得vD′==2 m/s< m/s,故小物块能通过D点。
(3)小物块恰好到F点,从E到F,由动能定理得-mgR(1-cos θ)=0-mv,解得vE= m/s,所以小物块在D点的速度范围为2 m/s≤vD< m/s。
答案 (1)5 N (2)能,过程见解析 (3)2 m/s≤vD< m/s
[针对训练3] 在温州市科技馆中,有个用来模拟天体运动的装置,其内部是一个类似锥形的漏斗容器,如图甲所示。现在该装置的上方固定一个半径为R的四分之一光滑管道AB,光滑管道下端刚好贴着锥形漏斗容器的边缘,如图乙所示。将一个质量为m的小球从管道的A点静止释放,小球从管道B点射出后刚好贴着锥形容器壁运动,由于摩擦阻力的作用,运动的高度越来越低,最后从容器底部的孔C掉下(轨迹大致如图乙虚线所示),已知小球离开C孔的速度为v,A到C的高度为H,重力加速度为g。求:
(1)小球到达B端的速度大小;
(2)小球在管口B端受到的支持力大小;
(3)小球在锥形漏斗表面运动的过程中克服摩擦阻力所做的功。
解析 (1)设小球到达B端的速度大小为vB,小球在从A端运动到B端的过程中,由动能定理可得mgR=mv
得vB=。
(2)设在B端小球受到的支持力大小为FN,
FN-mg=meq \f(v,R),得FN=3mg。
(3)设克服摩擦阻力做的功为Wf,根据动能定理mgH-Wf=mv2
得Wf=mgH-mv2。
答案 (1) (2)3mg (3)mgH-mv2
1.静止在粗糙水平面上的物块在水平向右的拉力作用下做直线运动,t=4 s 时停下,其v-t图像如图所示,已知物块与水平面间的动摩擦因数处处相同,则下列判断正确的是( )
A.整个过程中拉力做的功等于物块克服摩擦力做的功
B.整个过程中拉力做的功等于零
C.t=2 s时刻拉力的瞬时功率在整个过程中最大
D.t=1 s到t=3 s这段时间内拉力不做功
解析 全过程由动能定理得WF+WFf=0,所以A正确;因物块从静止开始运动,整个过程WF≠0,B错误;拉力的瞬时功率在1~3 s内相等,1 s末拉力的瞬时功率最大,C错误;t=1 s到t=3 s这段时间内,物块做匀速运动,F=Ff≠0,拉力做功W=Fx13≠0,D错误。
答案 A
2.如图所示,光滑圆轨道固定在竖直面内,一质量为m的小球沿轨道做完整的圆周运动,已知小球在最低点时对轨道的压力大小为FN1,在最高点时对轨道的压力大小为FN2。重力加速度大小为g,则FN1-FN2的值为( )
A.3mg B.4mg
C.5mg D.6mg
解析 在最低点有FN1-mg=meq \f(v,R),在最高点有FN2+mg=meq \f(v,R)。小球在运动过程中由动能定理-mg·2R=mv-mv,解得FN1-FN2=6mg。
答案 D
3.物体在恒定阻力作用下,以某初速度在水平面上沿直线滑行直到停止。以a、Ek、x和t分别表示物体运动的加速度大小、动能、位移的大小和运动的时间。则以下各图像中,能正确反映这一过程的是( )
解析 物体在恒定阻力作用下运动,其加速度不随时间和位移变化,选项A、B错误;由动能定理得-fx=Ek-Ek0,解得Ek=Ek0-fx,可知选项C正确;Ek=mv2=m(v0-at)2=ma2t2-mv0at+mv,Ek与t的关系图线为抛物线,选项D错误。
答案 C
4.质量m=1 kg的物体,在水平拉力F的作用下,沿粗糙水平面运动,在位移是4 m时,拉力F停止作用,运动到位移是8 m时物体停止,运动过程中Ek-x的图像如图所示,g取10 m/s2,求:
(1)物体和水平面间的动摩擦因数;
(2)拉力F的大小。
解析 (1)在运动的第二阶段,物体在位移x2=4 m内,动能由Ek=10 J变为零。由动能定理得-μmgx2=0-Ek;
故动摩擦因数
μ===0.25。
(2)在运动的第一阶段,物体位移x1=4 m,初动能Ek0=2 J,根据动能定理得Fx1-μmgx1=Ek-Ek0,所以F=4.5 N。
答案 (1)0.25 (2)4.5 N
5.2022年将在我国举办第二十四届冬奥会,跳台滑雪是其中最具观赏性的项目之一。某滑道示意图如图所示,长直助滑道AB与弯曲滑道BC平滑连接,滑道BC高h=10 m,C是半径R=20 m圆弧的最低点。质量m=60 kg的运动员从A处由静止开始匀加速下滑,加速度a=4.5 m/s2,到达B点时速度vB=30 m/s。取重力加速度g=10 m/s2。
(1)求长直助滑道AB的长度L;
(2)若不计BC段的阻力,画出运动员经过C点时的受力示意图,并求其所受支持力FN的大小。
解析 (1)根据匀变速直线运动公式v-v=2aL,
有L=eq \f(v-v,2a)=100 m。
(2)运动员经过C点时的受力示意图如图所示。
根据动能定理,运动员在BC段运动的过程中,有mgh=mv-mv
根据牛顿第二定律,有FN-mg=meq \f(v,R)
得FN=3 900 N。
答案 (1)100 m (2)见解析图 3 900 N
6.一个人站在距地面20 m的高处,将质量为0.2 kg的石块以v0=12 m/s的速度斜向上抛出,石块的初速度方向与水平方向之间的夹角为30°,g取10 m/s2,则:
(1)人抛石块过程中对石块做了多少功?
(2)若不计空气阻力,石块落地时的速度大小是多少?
(3)若落地时的速度大小为22 m/s,石块在空中运动过程中克服阻力做了多少功?
解析 (1)人抛石块的过程中,根据动能定理得
W=mv-0=14.4 J。
(2)不计空气阻力,石块从抛出至落地过程中,根据动能定理得mgh=mv-mv
解得v1≈23.32 m/s。
(3)从抛出至落地过程中,由动能定理得
mgh-Wf=eq \f(mv,2)-eq \f(mv,2),
解得Wf=mgh-eq \b\lc\(\rc\)(\a\vs4\al\co1(\f(mv,2)-\f(mv,2)))=6 J。
答案 (1)14.4 J (2)23.32 m/s (3)6 J
7.如图所示,光滑水平面AB与一半圆形轨道在B点相连,半圆形轨道位于竖直面内,其半径为R,一个质量为m的物块静止在水平面上,现向左推物块使其压紧弹簧,然后放手,物块在弹力作用下由静止获得一速度,当它经B点进入半圆形轨道瞬间,对轨道的压力为其重力的7倍,之后向上运动恰能完成半圆周运动到达C点,重力加速度为g。求:
(1)弹簧弹力对物块做的功;
(2)物块从B到C克服阻力所做的功;
(3)物块离开C点后,再落回到水平面上时的动能。
解析 (1)由动能定理得W=mv-0
在B点由牛顿第二定律得7mg-mg=meq \f(v,R)
解得W=3mgR。
(2)物块从B到C由动能定理得
Wf-2mgR=mv-mv
物块在C点时mg=meq \f(v,R)
解得Wf=-mgR,
即物块从B到C克服阻力做功为mgR。
(3)物块从C点平抛到水平面的过程中,由动能定理得
2mgR=Ek-mv,解得Ek=mgR。
答案 (1)3mgR (2)mgR (3)mgR
(新教材)2019—2020(浙江)人教版物理必修第二册同步学案讲义:第八章【拓展】动能定理的综合应用含答案
拓展:动能定理的综合应用
拓展点一 动能定理与牛顿运动定律的比较
1.理解比较
比较 牛顿第二定律 动能定理
作用 合外力与加速度的关系 合外力做的功与动能变化量的关系
公式 F=ma W=Ek2-Ek1
研究力和运动的关系 力的瞬间作用效果 力对空间的积累效果
运动过程中细节的考虑 考虑 不考虑
作用力 恒力 恒力或变力
2.应用比较
比较 牛顿运动定律 动能定理
相同点 确定研究对象,对物体进行受力分析和运动过程分析
适用条件 只能研究恒力作用下物体的运动的情况 对于物体在恒力或变力的作用下,物体做直线运动或曲线运动均适用
应用方法 要考虑运动过程的每一个细节,结合运动学公式 只考虑各力的做功情况及初、末状态的动能
运算方法 矢量运算 代数运算
[试题案例]
[例1] 如图所示,一质量为2 kg的铅球从离地面2 m高处自由下落,陷入沙坑2 cm深处,求沙子对铅球的平均阻力大小。(g取10 m/s2)
解析 法一 应用牛顿第二定律与运动学公式求解。
设铅球做自由落体运动到沙面时的速度为v,则有
v2=2gH。
在沙坑中的运动阶段,设铅球做匀减速运动的加速度大小为a,则有v2=2ah。
联立以上两式解得a=g。
设铅球在沙坑中运动时受到的平均阻力大小为Ff,由牛顿第二定律得Ff-mg=ma,所以Ff=mg+ma=·mg=×2×10 N=2 020 N。
法二 应用动能定理分段求解。
设铅球自由下落到沙面时的速度为v,由动能定理得mgH=mv2-0,设铅球在沙中受到的平均阻力大小为Ff,由动能定理得mgh-Ffh=0-mv2,联立以上两式得Ff=mg=2 020 N。
法三 应用动能定理全程求解。
铅球下落全过程都受重力,只有进入沙中铅球才受阻力Ff,重力做功WG=mg(H+h),阻力做功Wf=-Ffh。由动能定理得mg(H+h)-Ffh=0-0,代入数据得Ff=2 020 N。
答案 2 020 N
[针对训练1] 如图是冰上体育比赛“冰壶运动”的场地示意图(冰面水平)。在某次训练中,甲队员将质量m=20 kg的一个冰壶从左侧的A处向右推出,冰壶沿中心线运动到与A点相距为x=30 m的营垒中心O处恰好停下。此后,乙队员将完全相同的第二个冰壶同样在A处向右推出,冰壶从A处运动到O处经过的时间为t=10 s。已知两个冰壶与冰面间的动摩擦因数都为μ=0.02,冰壶都可视为质点,取g=10 m/s2。求:
(1)第一个冰壶被推出时的动能;
(2)第二个冰壶即将碰到第一个冰壶时的速度大小。
解析 (1)法一 牛顿第二定律
根据牛顿第二定律Ff=μmg=ma
根据运动学公式得v2=2ax=2μgx
动能的表达式Ek=mv2
联立并代入题给数据得Ek=μmgx=0.02×20×10×30 J=120 J。
法二 动能定理
对于甲队员推出的冰壶,由动能定理可得-μmgx=0-Ek1,代入数据得Ek1=120 J,故第一个冰壶被推出时的动能为120 J。
(2)第二个冰壶从A处运动到O处做匀减速运动,有μmg=ma,设冰壶在时间t内初、末速度分别为v2、v2′,则有v2′=v2-at,位移关系x=v2t-at2,代入数据解得第二个冰壶即将碰到第一个冰壶时的速度为v2′=2 m/s。
答案 (1)120 J (2)2 m/s
拓展点二 动能定理与图像的结合
分析动能定理和图像结合的问题时一定要弄清图像的物理意义,要特别注意图像的形状、交点、截距、斜率、面积等信息,并结合运动图像构建相应的物理模型,选择合理的规律求解有关问题。
[试题案例]
[例2] 如图甲所示,在水平地面上放置一个质量为m=4 kg的物体,让其在随位移均匀减小的水平推力作用下运动,推力F随位移x变化的图像如图乙所示,已
F与位移关系图线围成的面积表示功。
知物体与地面之间的动摩擦因数为μ=0.5,g取10 m/s2,求:
(1)出发时物体运动的加速度大小;
(2)物体能够运动的最大位移。
解析 (1)由牛顿第二定律得F-μmg=ma,
当推力F0=100 N时,物体所受的合力最大,加速度最大,代入数据得a=20 m/s2。
(2)根据图像得推力对物体做的功等于图线与x轴围成的面积,则推力对物体做功
W=F0x0=250 J,
根据动能定理可得W-μmgxm=0,
解得xm=12.5 m。
答案 (1)20 m/s2 (2)12.5 m
方法总结 “三步法”分析动能定理结合图像问题
[针对训练2] (多选)在平直公路上,汽车由静止开始做匀加速运动,当速度达到vm后立即关闭发动机直到停止,v-t图像如图所示。设汽车的牵引力为F,摩擦力为Ff,全过程中牵引力做功W1,克服摩擦力做功W2,则( )
A.F∶Ff=1∶3 B.F∶Ff=4∶1
C.W1∶W2=1∶1 D.W1∶W2=1∶3
解析 全过程初、末状态的动能都为零,
对全过程应用动能定理得W1-W2=0①
即W1=W2,选项C正确;
设物体在0~1 s内和1~4 s内运动的位移大小分别为s1、s2,则W1=Fs1②
W2=Ff(s1+s2)③
在v-t图像中,图像与时间轴包围的面积表示位移,由图像可知,s2=3s1④
由②③④式解得F∶Ff=4∶1,选项B正确。
答案 BC
拓展点三 利用动能定理处理曲线运动的多过程问题
1.平抛运动、圆周运动属于曲线运动,若只涉及位移和速度而不涉及时间,应优先考虑用动能定理列式求解。
2.用动能定理解题,关键是对研究对象进行准确的受力分析及运动过程分析,并画出物体运动过程的草图,让草图帮助我们理解物理过程和各量关系。
3.若物体的运动过程包含多个运动阶段,可分段应用动能定理,也可全程运用动能定理。若不涉及中间量,全程应用动能定理更简单、更方便。若涉及多个力做功,应注意力与位移的对应性。
[试题案例]
[例3] 如图所示,半径r1= m的圆弧轨道AB与水平轨道BC相切于B点,CD为r2=0.40 m的半圆轨道,另一半径R=1.00 m的圆弧轨道EF与CD靠近,E点略低于D点。一质量m=1 kg的小物块(可视为质点)从A点以初速度v0=2 m/s沿轨道下滑,在AB段运动过程中始终受到竖直向上的F=10 N的力作用,进入BC段后撤去。已知AB高度为h,BC长L=1.00 m,小物块与BC间动摩擦因数μ=0.2,其余光滑,EF轨道对应的圆心角θ=60°,所有轨道均固定在同一竖直平面内,不考虑小物块在各轨道相接处的速度大小的变化,忽略空气阻力,g取
10 m/s2。求:
(1)当小物块沿圆弧轨道AB运动到B点时,轨道对小物块的作用力大小;
(2)若小物块在B点的速度为5 m/s,且在刚进入BC段时撤去力F,请通过计算判断小物块能否通过D点;
(3)小物块能进入EF轨道,且不越过F点,小物块在D点的速度范围。
【审题指导】
题干关键点 提取信息
竖直向上的F=10 N的力 在AB段物块有恒力和重力做功
进入BC段后撤去F 在BC段物块只有摩擦力做功
物块能否通过D点 物块恰好过D点的条件是重力提供向心力
进入EF轨道,不越过F点 进入EF的最小速度对应过D点的最小速度,进入EF的最大速度对应到F点时速度为零
解析 (1)小物块从A到B,由动能定理得
mgh-Fh=mv-mv,解得vB=2 m/s。
在B点,由牛顿第二定律得F+FN-mg=meq \f(v,r1),
解得FN=5 N。
(2)假设小物块能从B到D,由动能定理得-2mgr2-μmgL=mv-mvB′2,解得vD= m/s。
若小物块恰好过D点,则mg=,解得vD′==2 m/s< m/s,故小物块能通过D点。
(3)小物块恰好到F点,从E到F,由动能定理得-mgR(1-cos θ)=0-mv,解得vE= m/s,所以小物块在D点的速度范围为2 m/s≤vD< m/s。
答案 (1)5 N (2)能,过程见解析 (3)2 m/s≤vD< m/s
[针对训练3] 在温州市科技馆中,有个用来模拟天体运动的装置,其内部是一个类似锥形的漏斗容器,如图甲所示。现在该装置的上方固定一个半径为R的四分之一光滑管道AB,光滑管道下端刚好贴着锥形漏斗容器的边缘,如图乙所示。将一个质量为m的小球从管道的A点静止释放,小球从管道B点射出后刚好贴着锥形容器壁运动,由于摩擦阻力的作用,运动的高度越来越低,最后从容器底部的孔C掉下(轨迹大致如图乙虚线所示),已知小球离开C孔的速度为v,A到C的高度为H,重力加速度为g。求:
(1)小球到达B端的速度大小;
(2)小球在管口B端受到的支持力大小;
(3)小球在锥形漏斗表面运动的过程中克服摩擦阻力所做的功。
解析 (1)设小球到达B端的速度大小为vB,小球在从A端运动到B端的过程中,由动能定理可得mgR=mv
得vB=。
(2)设在B端小球受到的支持力大小为FN,
FN-mg=meq \f(v,R),得FN=3mg。
(3)设克服摩擦阻力做的功为Wf,根据动能定理mgH-Wf=mv2
得Wf=mgH-mv2。
答案 (1) (2)3mg (3)mgH-mv2
1.静止在粗糙水平面上的物块在水平向右的拉力作用下做直线运动,t=4 s 时停下,其v-t图像如图所示,已知物块与水平面间的动摩擦因数处处相同,则下列判断正确的是( )
A.整个过程中拉力做的功等于物块克服摩擦力做的功
B.整个过程中拉力做的功等于零
C.t=2 s时刻拉力的瞬时功率在整个过程中最大
D.t=1 s到t=3 s这段时间内拉力不做功
解析 全过程由动能定理得WF+WFf=0,所以A正确;因物块从静止开始运动,整个过程WF≠0,B错误;拉力的瞬时功率在1~3 s内相等,1 s末拉力的瞬时功率最大,C错误;t=1 s到t=3 s这段时间内,物块做匀速运动,F=Ff≠0,拉力做功W=Fx13≠0,D错误。
答案 A
2.如图所示,光滑圆轨道固定在竖直面内,一质量为m的小球沿轨道做完整的圆周运动,已知小球在最低点时对轨道的压力大小为FN1,在最高点时对轨道的压力大小为FN2。重力加速度大小为g,则FN1-FN2的值为( )
A.3mg B.4mg
C.5mg D.6mg
解析 在最低点有FN1-mg=meq \f(v,R),在最高点有FN2+mg=meq \f(v,R)。小球在运动过程中由动能定理-mg·2R=mv-mv,解得FN1-FN2=6mg。
答案 D
3.物体在恒定阻力作用下,以某初速度在水平面上沿直线滑行直到停止。以a、Ek、x和t分别表示物体运动的加速度大小、动能、位移的大小和运动的时间。则以下各图像中,能正确反映这一过程的是( )
解析 物体在恒定阻力作用下运动,其加速度不随时间和位移变化,选项A、B错误;由动能定理得-fx=Ek-Ek0,解得Ek=Ek0-fx,可知选项C正确;Ek=mv2=m(v0-at)2=ma2t2-mv0at+mv,Ek与t的关系图线为抛物线,选项D错误。
答案 C
4.质量m=1 kg的物体,在水平拉力F的作用下,沿粗糙水平面运动,在位移是4 m时,拉力F停止作用,运动到位移是8 m时物体停止,运动过程中Ek-x的图像如图所示,g取10 m/s2,求:
(1)物体和水平面间的动摩擦因数;
(2)拉力F的大小。
解析 (1)在运动的第二阶段,物体在位移x2=4 m内,动能由Ek=10 J变为零。由动能定理得-μmgx2=0-Ek;
故动摩擦因数
μ===0.25。
(2)在运动的第一阶段,物体位移x1=4 m,初动能Ek0=2 J,根据动能定理得Fx1-μmgx1=Ek-Ek0,所以F=4.5 N。
答案 (1)0.25 (2)4.5 N
5.2022年将在我国举办第二十四届冬奥会,跳台滑雪是其中最具观赏性的项目之一。某滑道示意图如图所示,长直助滑道AB与弯曲滑道BC平滑连接,滑道BC高h=10 m,C是半径R=20 m圆弧的最低点。质量m=60 kg的运动员从A处由静止开始匀加速下滑,加速度a=4.5 m/s2,到达B点时速度vB=30 m/s。取重力加速度g=10 m/s2。
(1)求长直助滑道AB的长度L;
(2)若不计BC段的阻力,画出运动员经过C点时的受力示意图,并求其所受支持力FN的大小。
解析 (1)根据匀变速直线运动公式v-v=2aL,
有L=eq \f(v-v,2a)=100 m。
(2)运动员经过C点时的受力示意图如图所示。
根据动能定理,运动员在BC段运动的过程中,有mgh=mv-mv
根据牛顿第二定律,有FN-mg=meq \f(v,R)
得FN=3 900 N。
答案 (1)100 m (2)见解析图 3 900 N
6.一个人站在距地面20 m的高处,将质量为0.2 kg的石块以v0=12 m/s的速度斜向上抛出,石块的初速度方向与水平方向之间的夹角为30°,g取10 m/s2,则:
(1)人抛石块过程中对石块做了多少功?
(2)若不计空气阻力,石块落地时的速度大小是多少?
(3)若落地时的速度大小为22 m/s,石块在空中运动过程中克服阻力做了多少功?
解析 (1)人抛石块的过程中,根据动能定理得
W=mv-0=14.4 J。
(2)不计空气阻力,石块从抛出至落地过程中,根据动能定理得mgh=mv-mv
解得v1≈23.32 m/s。
(3)从抛出至落地过程中,由动能定理得
mgh-Wf=eq \f(mv,2)-eq \f(mv,2),
解得Wf=mgh-eq \b\lc\(\rc\)(\a\vs4\al\co1(\f(mv,2)-\f(mv,2)))=6 J。
答案 (1)14.4 J (2)23.32 m/s (3)6 J
7.如图所示,光滑水平面AB与一半圆形轨道在B点相连,半圆形轨道位于竖直面内,其半径为R,一个质量为m的物块静止在水平面上,现向左推物块使其压紧弹簧,然后放手,物块在弹力作用下由静止获得一速度,当它经B点进入半圆形轨道瞬间,对轨道的压力为其重力的7倍,之后向上运动恰能完成半圆周运动到达C点,重力加速度为g。求:
(1)弹簧弹力对物块做的功;
(2)物块从B到C克服阻力所做的功;
(3)物块离开C点后,再落回到水平面上时的动能。
解析 (1)由动能定理得W=mv-0
在B点由牛顿第二定律得7mg-mg=meq \f(v,R)
解得W=3mgR。
(2)物块从B到C由动能定理得
Wf-2mgR=mv-mv
物块在C点时mg=meq \f(v,R)
解得Wf=-mgR,
即物块从B到C克服阻力做功为mgR。
(3)物块从C点平抛到水平面的过程中,由动能定理得
2mgR=Ek-mv,解得Ek=mgR。
答案 (1)3mgR (2)mgR (3)mgR
