人教版七年级数学下册 8.3 实际问题与二元一次方程组课件(41张)
文档属性
| 名称 | 人教版七年级数学下册 8.3 实际问题与二元一次方程组课件(41张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-01 23:48:26 | ||
图片预览







文档简介
(共41张PPT)
只闻隔壁人分银,不知多少银和人;
每人 7 两少 7两,每人半斤多半斤;
试问各位善算者,多少人分多少银?
(注:这里的斤是指市斤,1市斤=10两)
我国古代数学问题
新课导入
1.学习了用二元一次方程组解决实际问题;
2.熟练找等量关系;
3.练习根据等量关系列方程组.
知识与能力
教学目标
1.能够熟练的找出实际应用题中的两个等量关系,并能够根据等量关系列出相应的二元一次方程组;
2.强调“转化”思想在应用题中的应用,训练分析实际问题的能力;
3.能够列出二元一次方程组解决简单的实际问题.能够初步联系日常生活或生产实际提出可以利用二元一次方程来解决的实际问题,并能正确地表述问题及解决问题的过程.
过程与方法
1.在用方程组解决实际问题的过程中,体验数学的实用性,提高学习数学的兴趣;
2.在探讨解决问题的过程中,敢于发表自己的见解,理解他人的看法并与他人交流.
情感态度与价值观
经历和体验把实际问题转化为二元一次方程组的过程,用二元一次方程组解决实际问题.
把实际问题转化为二元一次方程组.
重点
难点
教学重难点
解:设平均每只大牛和每只小牛1天各约用饲料xkg和ykg.
例1 养牛场原有30只大牛和15只小牛,1天约需用饲料675 kg;一周后又购进12只大牛和5只小牛,这时1天约需要饲料940 kg.饲养员李大叔估计平均每只大牛1天约需要饲料18~20 kg,每只小牛1天约需要7~8 kg.你能否通过计算检验他的估计?
(1)30只大牛1天所需饲料+15只小牛1天所需饲料=1天的饲料总量;
(2)42只大牛1天所需饲料+20只小牛1天所需饲料=后来1天的饲料总量.
30x+15y=675
42x+20y=940
解这个方程组,得
因此,饲养员李大叔对大牛的食量估计较准确,对小牛的食量估计偏高.
x=20
y=5
答:平均每只大牛和每只小牛1天各约用饲料20kg和5kg.
例2 据以往的统计资料,甲、乙两种作物的单位面积产量的比是1:1.5,现要在一块长200m,宽100m的长方形土地上种植这两种作物,怎样把这块地分为两个长方形,使甲、乙两种作物的总产量的比是 3 : 4 (结果取整数)?
A
B
C
D
解法一:设AE为 x 米,BE为 y 米,由题意得:
A
B
C
D
E
┓
x
y
解方程组,得:
由题意取值:
答: 过长方形土地的长边上离一端约106米处,把这块地分为两个长方形,较大一块地种甲种作物,较小一块地种乙种作物.
x + y=200
100 x: (1.5×100 y )=3:4
x=
y=
x≈ 106
y≈ 94
A
B
C
D
E
┓
y
x
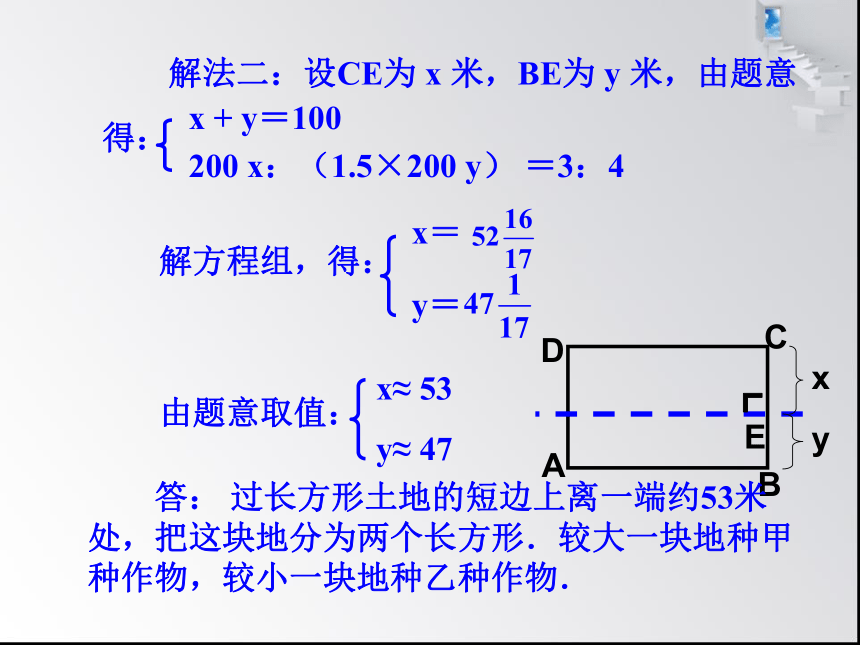
解法二:设CE为 x 米,BE为 y 米,由题意得:
解方程组,得:
由题意取值:
答: 过长方形土地的短边上离一端约53米处,把这块地分为两个长方形.较大一块地种甲种作物,较小一块地种乙种作物.
x=
y=
x≈ 53
y≈ 47
x + y=100
200 x:(1.5×200 y) =3:4
A
B
铁路120km
公路10km
.
长青化工厂
铁路110km
公路20km
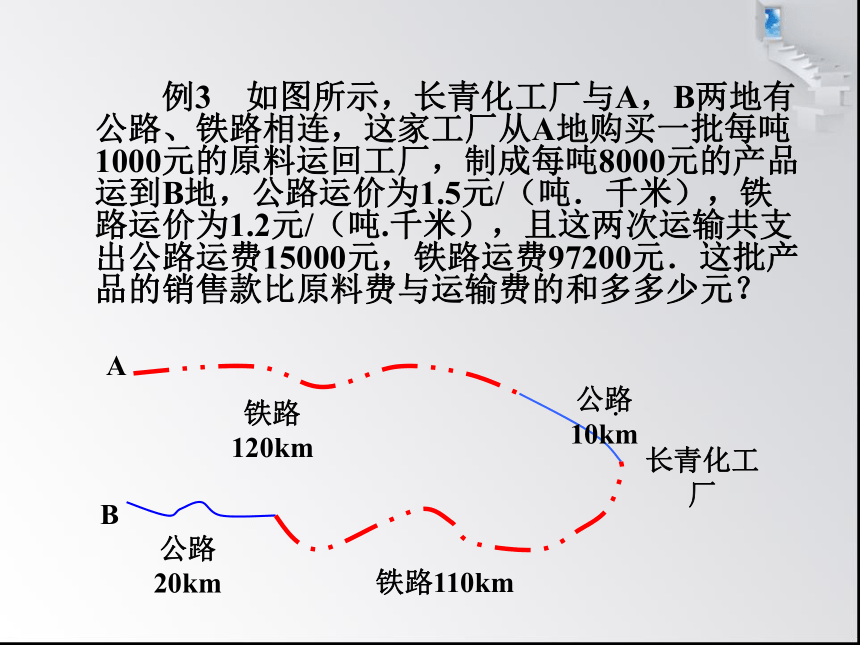
例3 如图所示,长青化工厂与A,B两地有公路、铁路相连,这家工厂从A地购买一批每吨1000元的原料运回工厂,制成每吨8000元的产品运到B地,公路运价为1.5元/(吨.千米),铁路运价为1.2元/(吨.千米),且这两次运输共支出公路运费15000元,铁路运费97200元.这批产品的销售款比原料费与运输费的和多多少元?
解:设制成产品x吨,原料y吨,由题意得
1.5×(20x+10y)=15000
1.2×(110x+120y)=97200
x=300
y = 400
解方程组,得
答:这批产品的销售款比原料费与运输费的和多1887800元.
应用二元一次方程组解决实际问题的基本步骤:
理解问题
制定计划
执行计划
回顾检查
实际问题
分析
抽象
方程(组)
求解
检验
问题解决
(2)设:设未知数,可以直接设之,也可以
间接 设之;
(5)答:检验解的正确性和合理性,写出答
案.
(4)解:解方程组,求出未知数的值;
(3)列:根据题中的等量关系列方程组;
(1)审:审题,弄清题意及题中的数量关系;
例4 MP3和书包单价之和是456元,且MP3的单价比书包单价的4倍少16元,试计算MP3和书包的单价各是多少元?
解:设MP3单价x元,书包单价y元.根据题意得
x+y=456
x= 4y -16
x=368
y= 88
答:mp3单价368元,书包单价88元.
解得,
(1)若某商场同时购进该厂家两种不同型号电视机共80台,正好用去15万元,请你设计出几种不同的进货方案,并说明理由.
例5 某厂家生产三种不同型号的电视机,出厂价甲种每台1500元,乙种每台2000元,丙种每台2500元.
(2)商场销售一台甲种电视机可获利160元,销售一台乙种电视机可获利210元,销售一台丙种电视机可获利260元.在同时购进两种不同型号电视机的方案中,为使销售时获利最多,你选择哪种进货方案?
x+y=80
1500x+2000y=150000
x=20
y=60
解:(1)设购进甲种电视机x台,乙种电视机y台,则有
解方程组,得
舍去
y+z=80
2000y+2500z=150000
y=100
z=-20
设购进乙种电视机y台,丙种电视机z台,则有
解方程组,得
x+z=80
1500x+2500z=150000
x=50
z=30
设购进甲种电视机x台,丙种电视机z台,则有
解方程组,得
答:有两种进货方案,购进甲种电视机20台,乙种电视机60台;或购进甲种电视机50台,丙种电视机30台.
(2)只购进甲种电视机20台,乙种电视机60台:
只购进甲种电视机50台,丙种电视机30台 :
获利:
20×160+60×260=18800(元)
50×160+30×260=15800(元)
获利:
答:只购进甲种电视机20台,丙种电视机60台获利最多.
例6 动物园门票价格如下表所示:
购票人数 1~50人 51~100人 100人以上
每人门票价 14元 12元 10元
某校初一(1),(2)两个班共104人去植物园春游,其中(1)班人数较少,不到50人,(2)班人数较多,有50多人.经估算如果两班都以班为单位分别购票,则一共应付1344元.试问两个班各有多少名学生?他们如何购票比较合算?
解:设(1)班有x名学生,(2)班有y名学生,根据题意,得
x+y=104
14x+12y=1344
解方程组,得
x=48
y=56
若两个班集体购票,则需要花费
10×104=1040(元)
答:甲班有48名学生,乙班有56名学生,两个班集体购票比较合算.
例7 一根金属棒在0℃时的长度是q (m),温度每升高1℃,它就伸长p (m).当温度为t ℃时,金属棒的长度可用公式l=pt+q计算.已测得当t =100℃时,l =2.002m;当t =500℃时,l=2.01m.
(1)求p,q的值;
(2)若这根金属棒加热后长度伸长到2.016m,问这时金属棒的温度是多少?
p=0.00002
q=2
100p+q=2.002 ①
500p+q=2.01 ②
解:(1)根据题意,
②-①,得400p=0.008,解得p=0.00002
把p=0.00002代入①,
得0.002+q=2.002,解得q=2
即
答:p=0.00002,q=2
(2)由(1),得l=0.00002t+2
金属棒加热后,长度伸长到2.016m,即当l=2.016m时,2.016=0.00002t+2,
解这个一元一次方程,得t=800(℃)
答:此时金属棒得温度是800 ℃.
例8 第一个数的8%与第二个数的9%的和是67,第一个数的9%与第二个数的8%的差是19.求这两个数.
即
解此方程组,得
8% x+9% y=67
9% x-8% y=21
8x+9y=6700
9x-8y=2100
x=500
y=300
答:第一个数为500,第二个数为300.
解:设第一个数为x,第二个数为y,依题意,得
例9 两种酒精,甲种含水15%,乙种含水5%,现在要配成含水12%的酒精1000克.每种酒精各需多少克?
x+y=1000
15% x+5% y=1000×12%
即
x+y=1000
3x+y=2400
解此方程组,得
x=700
y=300
答:甲种酒精取700克,乙种酒精取300克.
解:设甲种酒精取x克,乙种酒精取y克.依题意,得
例10 有两种合金,第一种合金含金90%,第二种合金含金80%,这两种合金各取多少克,熔化以后才能得到含金82.5%的合金200克?
解:设第一种合金取x克,第二种合金取y克.
依题意,得
x+y=200
90% x+80% y=200×82.5%
即
x+y=200
9x+8y=1650
解此方程组,得
x=50
y=150
答:第一种合金取50克,第二种合金取150克.
例11 小刚骑摩托车在公路上高速匀速行驶,8:00时看到里程碑上的数是一个两位数,它的数字之和是7;9:00时看里程碑上的两位数与8:00时看到的个位数和十位数颠倒了;10:00时看到里程碑上的数比8:00时看到的两位数中间多了个零,小刚在8:00时看到里程碑上的数字是多少?
解:设小刚在8:00时看到的数字的十位数字是x,个位的数字是y,那么
x+y=7
(10y+x)-(10x+y)=(100x+y)-(10y+x)
答:小刚在8:00时看到的数字是16.
x=1
y=6
解方程组,得
例12 25名工人按定额完成了2200件产品,其中三级工每人每天定额200件,二级工每人每天定额60件.若这25名工人只有二级工与三级工,问二级工与三级工各有多少名?
解:设二级工有x名,三级工有y名.根据题意,有
解这个方程组,得
答:二级工有20名,三级工有5名.
x+y=25
60x+200y=2200
x=20
y=5
例13 欲将某河上游A地的一部分牧场改为林场.改变后,林场和牧场共有160公顷, 林场面积是牧场面积的7倍, 试问完成后林场、牧场的面积各为多少公顷?
解:设完成后林场面积为x公顷,牧场面积为y公顷,根据题意,有
解这个方程组,得
答:完成后林场面积为140公顷,牧场面积为20公顷.
x+y=160
x=7y
x=140
y=20
例14 某船的载重为300吨,容积这1000米3. 现有甲、乙两种货物要运,其中甲种货物每吨体积为7米3 ,乙种货物每吨体积为2米3 ,若要充分利用这艘船的载重与容积,甲、乙两种货物应各装多少吨?
解:设甲、乙两种货物应分别装x吨、y吨,根据题意,有
答:甲、乙两种货物应分别装80吨、220吨.
解这个方程组,得
x+y=300
7x+2y=1000
x=80
y=220
例15 通过对一份中学生营养快餐的检测,得到以下信息:
①快餐总质量为600g;
②快餐的成分:蛋白质、碳水化合物、脂肪、矿物质
③蛋白质和脂肪含量占50%;矿物质的含量是脂肪含量的2倍;蛋白质和碳水化合物含量占85%
根据上述数据分别求出营养快餐中蛋白质、碳水化合物、脂肪、矿物质的质量.
解:设一份营养快餐中的蛋白质为xg,脂肪为yg,则碳水化合物为(600×85%-x)g,矿物质为2y,根据题意, 得
解这个方程组,得:
x+y=600×50%
(600×85%-x)+2y=600×50%
x=270
y=30
∴ 2y=2×30=60 (g),
600×85%-x=240 (g)
答:营养快餐中蛋白质的质量是270g、碳水化合物的质量是240g、脂肪的质量是30g、矿物质的质量是60g.
列方程组解应用题的一般步骤:
审:弄情题目中的数量关系, 设出两个未知数.
列:列出方程组
分析题意,找出两个等量关系
用含未知数的一次式表示有关的量
根据等量关系列出方程组
解:解出方程组,求出未知数的值.
验:检验求得的值是否正确和符合实际情形.
答:写出答案.
课堂小结
1.一条船顺流航行是逆流航行的速度的3倍,这
条船在静水中的航速与水的流速之比为( )
A.3:1 B.2:1
C.4:1 D.5:2
2.小聪存入银行人民币若干元,年利率为2.25%,
一年到期后将缴纳利息税72元(税率为利息的
20%),则他存入的人民币为( )
A.1600元 B.16000元
C.360元 D.3600元
B
B
随堂练习
3.某工厂去年的得润(总产值-总支出)为200万
元,今年总产值比去年增加了20%,总支出
比去年减少了10%,今年的利润为420万元.
去年的总产值为_____万元,总支出为______
万元.
800
600
4.有两种药水,一种浓度为60%,另一种浓度
为90%,现要配制浓度为70%的药水300g,
则需 60%浓度的药水____g,90%浓度的药
水_______克.
100
200
5.一、二两班共有100名学生,他们的体育达标
率为81%,如果一班学生的体育达标率为
87.5%,二班的达标率为75%,那么一、二两
班的学生数分别为_____、_____.
48
52
6.40㎏含铜60%的合金和含铜80%的合金混在
一起制成含铜75%的合金.则原来每种合金
分别重____㎏、_____㎏.
10
30
7.有一批机器零件共418个,若甲先做2天,乙
再加入合作,则再做2天可超产2个;若乙先做
3天, 然后两人再共做2天,则还有 8个未完
成.则甲每天做____个零件,乙每天做____个
零件.
80
50
8.几个同学分铅笔,若其中有6人各取4枝,其
余的人每人取3枝,则还剩14枝;若每人分5
支,则恰好分完,问分铅笔的同学多少人?
铅笔有多少枝?
解:设同学有x人,铅笔有y枝,根据题意,有
答:同学有10人,铅笔有50枝.
解这个方程组,得
x=10,
y=50.
y=6×4+3(x-4)+14,
y=5x.
9.某蔬菜公司收购到某种蔬菜260吨,准备加工
后上市销售.该公司的加工能力是:每天可
以精加工8吨或粗加工18吨.现计划用20天完
成加工任务,该公司应安排几天粗加工,几
天精加工,才能按期完成任务?如果每吨蔬
菜粗加工后的利润为1000元,精加工后为2000
元,那么该公司出售这些加工后的蔬菜共可获
利多少元?
解:设应安排x天精加工,y天粗加工.根据题意,得
x+y=20,
8x+18y=260.
解这个方程组,得
x=10,
y=10.
出售这些加工后的蔬菜一共可获利
1000×18×10+2000×8×10
=340000 (元)
答:应安排10天精加工,10天粗加工,加工后出售共可获利340 000元.
只闻隔壁人分银,不知多少银和人;
每人 7 两少 7两,每人半斤多半斤;
试问各位善算者,多少人分多少银?
(注:这里的斤是指市斤,1市斤=10两)
我国古代数学问题
新课导入
1.学习了用二元一次方程组解决实际问题;
2.熟练找等量关系;
3.练习根据等量关系列方程组.
知识与能力
教学目标
1.能够熟练的找出实际应用题中的两个等量关系,并能够根据等量关系列出相应的二元一次方程组;
2.强调“转化”思想在应用题中的应用,训练分析实际问题的能力;
3.能够列出二元一次方程组解决简单的实际问题.能够初步联系日常生活或生产实际提出可以利用二元一次方程来解决的实际问题,并能正确地表述问题及解决问题的过程.
过程与方法
1.在用方程组解决实际问题的过程中,体验数学的实用性,提高学习数学的兴趣;
2.在探讨解决问题的过程中,敢于发表自己的见解,理解他人的看法并与他人交流.
情感态度与价值观
经历和体验把实际问题转化为二元一次方程组的过程,用二元一次方程组解决实际问题.
把实际问题转化为二元一次方程组.
重点
难点
教学重难点
解:设平均每只大牛和每只小牛1天各约用饲料xkg和ykg.
例1 养牛场原有30只大牛和15只小牛,1天约需用饲料675 kg;一周后又购进12只大牛和5只小牛,这时1天约需要饲料940 kg.饲养员李大叔估计平均每只大牛1天约需要饲料18~20 kg,每只小牛1天约需要7~8 kg.你能否通过计算检验他的估计?
(1)30只大牛1天所需饲料+15只小牛1天所需饲料=1天的饲料总量;
(2)42只大牛1天所需饲料+20只小牛1天所需饲料=后来1天的饲料总量.
30x+15y=675
42x+20y=940
解这个方程组,得
因此,饲养员李大叔对大牛的食量估计较准确,对小牛的食量估计偏高.
x=20
y=5
答:平均每只大牛和每只小牛1天各约用饲料20kg和5kg.
例2 据以往的统计资料,甲、乙两种作物的单位面积产量的比是1:1.5,现要在一块长200m,宽100m的长方形土地上种植这两种作物,怎样把这块地分为两个长方形,使甲、乙两种作物的总产量的比是 3 : 4 (结果取整数)?
A
B
C
D
解法一:设AE为 x 米,BE为 y 米,由题意得:
A
B
C
D
E
┓
x
y
解方程组,得:
由题意取值:
答: 过长方形土地的长边上离一端约106米处,把这块地分为两个长方形,较大一块地种甲种作物,较小一块地种乙种作物.
x + y=200
100 x: (1.5×100 y )=3:4
x=
y=
x≈ 106
y≈ 94
A
B
C
D
E
┓
y
x
解法二:设CE为 x 米,BE为 y 米,由题意得:
解方程组,得:
由题意取值:
答: 过长方形土地的短边上离一端约53米处,把这块地分为两个长方形.较大一块地种甲种作物,较小一块地种乙种作物.
x=
y=
x≈ 53
y≈ 47
x + y=100
200 x:(1.5×200 y) =3:4
A
B
铁路120km
公路10km
.
长青化工厂
铁路110km
公路20km
例3 如图所示,长青化工厂与A,B两地有公路、铁路相连,这家工厂从A地购买一批每吨1000元的原料运回工厂,制成每吨8000元的产品运到B地,公路运价为1.5元/(吨.千米),铁路运价为1.2元/(吨.千米),且这两次运输共支出公路运费15000元,铁路运费97200元.这批产品的销售款比原料费与运输费的和多多少元?
解:设制成产品x吨,原料y吨,由题意得
1.5×(20x+10y)=15000
1.2×(110x+120y)=97200
x=300
y = 400
解方程组,得
答:这批产品的销售款比原料费与运输费的和多1887800元.
应用二元一次方程组解决实际问题的基本步骤:
理解问题
制定计划
执行计划
回顾检查
实际问题
分析
抽象
方程(组)
求解
检验
问题解决
(2)设:设未知数,可以直接设之,也可以
间接 设之;
(5)答:检验解的正确性和合理性,写出答
案.
(4)解:解方程组,求出未知数的值;
(3)列:根据题中的等量关系列方程组;
(1)审:审题,弄清题意及题中的数量关系;
例4 MP3和书包单价之和是456元,且MP3的单价比书包单价的4倍少16元,试计算MP3和书包的单价各是多少元?
解:设MP3单价x元,书包单价y元.根据题意得
x+y=456
x= 4y -16
x=368
y= 88
答:mp3单价368元,书包单价88元.
解得,
(1)若某商场同时购进该厂家两种不同型号电视机共80台,正好用去15万元,请你设计出几种不同的进货方案,并说明理由.
例5 某厂家生产三种不同型号的电视机,出厂价甲种每台1500元,乙种每台2000元,丙种每台2500元.
(2)商场销售一台甲种电视机可获利160元,销售一台乙种电视机可获利210元,销售一台丙种电视机可获利260元.在同时购进两种不同型号电视机的方案中,为使销售时获利最多,你选择哪种进货方案?
x+y=80
1500x+2000y=150000
x=20
y=60
解:(1)设购进甲种电视机x台,乙种电视机y台,则有
解方程组,得
舍去
y+z=80
2000y+2500z=150000
y=100
z=-20
设购进乙种电视机y台,丙种电视机z台,则有
解方程组,得
x+z=80
1500x+2500z=150000
x=50
z=30
设购进甲种电视机x台,丙种电视机z台,则有
解方程组,得
答:有两种进货方案,购进甲种电视机20台,乙种电视机60台;或购进甲种电视机50台,丙种电视机30台.
(2)只购进甲种电视机20台,乙种电视机60台:
只购进甲种电视机50台,丙种电视机30台 :
获利:
20×160+60×260=18800(元)
50×160+30×260=15800(元)
获利:
答:只购进甲种电视机20台,丙种电视机60台获利最多.
例6 动物园门票价格如下表所示:
购票人数 1~50人 51~100人 100人以上
每人门票价 14元 12元 10元
某校初一(1),(2)两个班共104人去植物园春游,其中(1)班人数较少,不到50人,(2)班人数较多,有50多人.经估算如果两班都以班为单位分别购票,则一共应付1344元.试问两个班各有多少名学生?他们如何购票比较合算?
解:设(1)班有x名学生,(2)班有y名学生,根据题意,得
x+y=104
14x+12y=1344
解方程组,得
x=48
y=56
若两个班集体购票,则需要花费
10×104=1040(元)
答:甲班有48名学生,乙班有56名学生,两个班集体购票比较合算.
例7 一根金属棒在0℃时的长度是q (m),温度每升高1℃,它就伸长p (m).当温度为t ℃时,金属棒的长度可用公式l=pt+q计算.已测得当t =100℃时,l =2.002m;当t =500℃时,l=2.01m.
(1)求p,q的值;
(2)若这根金属棒加热后长度伸长到2.016m,问这时金属棒的温度是多少?
p=0.00002
q=2
100p+q=2.002 ①
500p+q=2.01 ②
解:(1)根据题意,
②-①,得400p=0.008,解得p=0.00002
把p=0.00002代入①,
得0.002+q=2.002,解得q=2
即
答:p=0.00002,q=2
(2)由(1),得l=0.00002t+2
金属棒加热后,长度伸长到2.016m,即当l=2.016m时,2.016=0.00002t+2,
解这个一元一次方程,得t=800(℃)
答:此时金属棒得温度是800 ℃.
例8 第一个数的8%与第二个数的9%的和是67,第一个数的9%与第二个数的8%的差是19.求这两个数.
即
解此方程组,得
8% x+9% y=67
9% x-8% y=21
8x+9y=6700
9x-8y=2100
x=500
y=300
答:第一个数为500,第二个数为300.
解:设第一个数为x,第二个数为y,依题意,得
例9 两种酒精,甲种含水15%,乙种含水5%,现在要配成含水12%的酒精1000克.每种酒精各需多少克?
x+y=1000
15% x+5% y=1000×12%
即
x+y=1000
3x+y=2400
解此方程组,得
x=700
y=300
答:甲种酒精取700克,乙种酒精取300克.
解:设甲种酒精取x克,乙种酒精取y克.依题意,得
例10 有两种合金,第一种合金含金90%,第二种合金含金80%,这两种合金各取多少克,熔化以后才能得到含金82.5%的合金200克?
解:设第一种合金取x克,第二种合金取y克.
依题意,得
x+y=200
90% x+80% y=200×82.5%
即
x+y=200
9x+8y=1650
解此方程组,得
x=50
y=150
答:第一种合金取50克,第二种合金取150克.
例11 小刚骑摩托车在公路上高速匀速行驶,8:00时看到里程碑上的数是一个两位数,它的数字之和是7;9:00时看里程碑上的两位数与8:00时看到的个位数和十位数颠倒了;10:00时看到里程碑上的数比8:00时看到的两位数中间多了个零,小刚在8:00时看到里程碑上的数字是多少?
解:设小刚在8:00时看到的数字的十位数字是x,个位的数字是y,那么
x+y=7
(10y+x)-(10x+y)=(100x+y)-(10y+x)
答:小刚在8:00时看到的数字是16.
x=1
y=6
解方程组,得
例12 25名工人按定额完成了2200件产品,其中三级工每人每天定额200件,二级工每人每天定额60件.若这25名工人只有二级工与三级工,问二级工与三级工各有多少名?
解:设二级工有x名,三级工有y名.根据题意,有
解这个方程组,得
答:二级工有20名,三级工有5名.
x+y=25
60x+200y=2200
x=20
y=5
例13 欲将某河上游A地的一部分牧场改为林场.改变后,林场和牧场共有160公顷, 林场面积是牧场面积的7倍, 试问完成后林场、牧场的面积各为多少公顷?
解:设完成后林场面积为x公顷,牧场面积为y公顷,根据题意,有
解这个方程组,得
答:完成后林场面积为140公顷,牧场面积为20公顷.
x+y=160
x=7y
x=140
y=20
例14 某船的载重为300吨,容积这1000米3. 现有甲、乙两种货物要运,其中甲种货物每吨体积为7米3 ,乙种货物每吨体积为2米3 ,若要充分利用这艘船的载重与容积,甲、乙两种货物应各装多少吨?
解:设甲、乙两种货物应分别装x吨、y吨,根据题意,有
答:甲、乙两种货物应分别装80吨、220吨.
解这个方程组,得
x+y=300
7x+2y=1000
x=80
y=220
例15 通过对一份中学生营养快餐的检测,得到以下信息:
①快餐总质量为600g;
②快餐的成分:蛋白质、碳水化合物、脂肪、矿物质
③蛋白质和脂肪含量占50%;矿物质的含量是脂肪含量的2倍;蛋白质和碳水化合物含量占85%
根据上述数据分别求出营养快餐中蛋白质、碳水化合物、脂肪、矿物质的质量.
解:设一份营养快餐中的蛋白质为xg,脂肪为yg,则碳水化合物为(600×85%-x)g,矿物质为2y,根据题意, 得
解这个方程组,得:
x+y=600×50%
(600×85%-x)+2y=600×50%
x=270
y=30
∴ 2y=2×30=60 (g),
600×85%-x=240 (g)
答:营养快餐中蛋白质的质量是270g、碳水化合物的质量是240g、脂肪的质量是30g、矿物质的质量是60g.
列方程组解应用题的一般步骤:
审:弄情题目中的数量关系, 设出两个未知数.
列:列出方程组
分析题意,找出两个等量关系
用含未知数的一次式表示有关的量
根据等量关系列出方程组
解:解出方程组,求出未知数的值.
验:检验求得的值是否正确和符合实际情形.
答:写出答案.
课堂小结
1.一条船顺流航行是逆流航行的速度的3倍,这
条船在静水中的航速与水的流速之比为( )
A.3:1 B.2:1
C.4:1 D.5:2
2.小聪存入银行人民币若干元,年利率为2.25%,
一年到期后将缴纳利息税72元(税率为利息的
20%),则他存入的人民币为( )
A.1600元 B.16000元
C.360元 D.3600元
B
B
随堂练习
3.某工厂去年的得润(总产值-总支出)为200万
元,今年总产值比去年增加了20%,总支出
比去年减少了10%,今年的利润为420万元.
去年的总产值为_____万元,总支出为______
万元.
800
600
4.有两种药水,一种浓度为60%,另一种浓度
为90%,现要配制浓度为70%的药水300g,
则需 60%浓度的药水____g,90%浓度的药
水_______克.
100
200
5.一、二两班共有100名学生,他们的体育达标
率为81%,如果一班学生的体育达标率为
87.5%,二班的达标率为75%,那么一、二两
班的学生数分别为_____、_____.
48
52
6.40㎏含铜60%的合金和含铜80%的合金混在
一起制成含铜75%的合金.则原来每种合金
分别重____㎏、_____㎏.
10
30
7.有一批机器零件共418个,若甲先做2天,乙
再加入合作,则再做2天可超产2个;若乙先做
3天, 然后两人再共做2天,则还有 8个未完
成.则甲每天做____个零件,乙每天做____个
零件.
80
50
8.几个同学分铅笔,若其中有6人各取4枝,其
余的人每人取3枝,则还剩14枝;若每人分5
支,则恰好分完,问分铅笔的同学多少人?
铅笔有多少枝?
解:设同学有x人,铅笔有y枝,根据题意,有
答:同学有10人,铅笔有50枝.
解这个方程组,得
x=10,
y=50.
y=6×4+3(x-4)+14,
y=5x.
9.某蔬菜公司收购到某种蔬菜260吨,准备加工
后上市销售.该公司的加工能力是:每天可
以精加工8吨或粗加工18吨.现计划用20天完
成加工任务,该公司应安排几天粗加工,几
天精加工,才能按期完成任务?如果每吨蔬
菜粗加工后的利润为1000元,精加工后为2000
元,那么该公司出售这些加工后的蔬菜共可获
利多少元?
解:设应安排x天精加工,y天粗加工.根据题意,得
x+y=20,
8x+18y=260.
解这个方程组,得
x=10,
y=10.
出售这些加工后的蔬菜一共可获利
1000×18×10+2000×8×10
=340000 (元)
答:应安排10天精加工,10天粗加工,加工后出售共可获利340 000元.
