人教版七年级数学下册8.4 三元一次方程组的解法 课件(27张)
文档属性
| 名称 | 人教版七年级数学下册8.4 三元一次方程组的解法 课件(27张) |  | |
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-01 23:55:40 | ||
图片预览







文档简介
(共27张PPT)
问题:甲、乙、丙三数的和是33,甲数比乙数大
2,甲数的两倍与丙数的和比乙数大24,
求这三个数.
思考:题目中有几个未知数?含有几个相等关系?
你能根据题意列出几个方程?
根据题意,列方程组:
讨论:上面方程组具有什么特点?
新课导入
8.4 三元一次方程组的解法
1.了解三元一次方程组的概念;
2.熟练掌握简单的三元一次方程组的解法;
3.能选择简便,特殊的解法解特殊的三元一次方程组;
4.掌握解三元一次方程组化三元为二元或一元的思路;
5.培养分析能力,能根据题目的特点,确定消元方法、消元对象;
6.培养计算能力、训练解题技巧.
知识与能力
教学目标
1.通过用代入消元法,加减消元法解简单的三元一次方程组的训练及选择合理,简捷的方法解方程组,培养运算能力;
2.通过三元一次方程组消元后转化为二元一次方程组,再消元转化为一元一次方程及将一些代数问题转化为方程组问题的方法的学习,培养初步运用转化思想去解决问题,发展思维能力.
过程与方法
渗透消元的思想,培养学习兴趣.
情感态度与价值观
1.用代入法或加减法解三元一次方程组;
2.进一步熟悉方程组时“消元”的基本思想和灵活运用代入法、加减法等重要方法.
针对方程组的特点,选择最好的解法.
重点
难点
教学重难点
方程组中含有三个相同的未知数,每个方程中含未知数的项的次数都是1,并且一共有三个方程,像这样的方程组叫做三元一次方程组.
知识要点
有一个三位数,已知个位上的数比十位上的数大2,十位上的数比百位上的数大3,且个位、十位、百位上的数的和为17,求这个三位数是多少?
解:设个位上的数是x、十位上的数是y、百位上的数是z,根据题意,得
x-y=2 ①
y-z=3 ②
x+y+z=17 ③
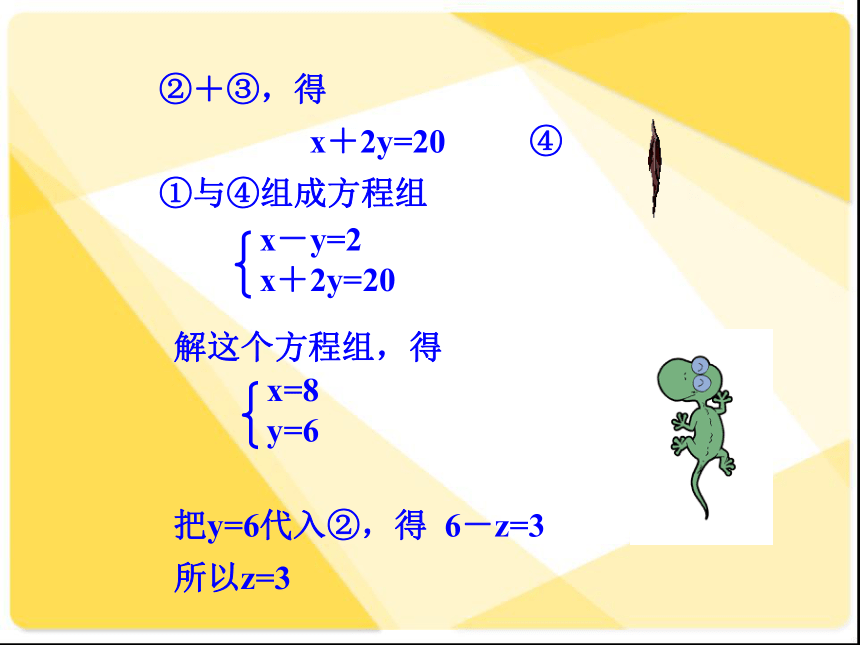
②+③,得
x+2y=20 ④
①与④组成方程组
x-y=2
x+2y=20
解这个方程组,得
x=8
y=6
把y=6代入②,得 6-z=3
所以z=3
所以,这个三元一次方程组的解是
x=8
y=6
z=3
答:这个三位数是368.
①利用代入法或加减法,消去一个未知数,得出一个二元一次方程组;
②解这个二元一次方程组,求得两个未知数的值;
③将这两个未知数的值代入原方程中较简单的一个方程,求出第三个未知数的值,把这三个数写在一起的就是所求的三元一次方程组的解.
解三元一次方程组的步骤:
例1 解三元一次方程组
3x-4y+z=11 ①
5y-z=6 ②
4x+2y-3z=12 ③
解:①×4-③×3,得
-22y+13z=8 ④
②与④组成方程组
5y-z=6
-22y+13z=8
解这个方程组,得
y=2
z=4
把y=2 ,z=4代入①,得
3x-4×2+4=11
所以 x=5
因此,三元一次方程组的解是
x=5
y=2
z=4
例2 解三元一次方程组
x+y=7 ①
y+z=9 ②
z+x=8 ③
解:①+②+③得2x+2y+2z=24
即 x+y+z=12 ④
④-①得 z=5
④-②得 x=3
④-③得 y=4
x=3
y=4
z=5
因此,三元一次方程组的解为
例3 解方程组
x:y:z=2:3:5
x+y+z=200
解:此方程组即为
3x=2y ①
3z=5y ②
x+y+z=100 ③
即:
③×3 -① - ②,得 y=75
把y=75分别代入①②,得
3x=2×75
所以x=50
3z=5×75
所以Z=125
因此,三元一次方程组的解为
x=50
y=75
z=125
例4 在等式y=ax2+bx+c中,当x=1时,y=9;当x=2时,y=26;当x=0时,y=6.求a,b,c的值.
解:根据题意,得三元一次方程组
①
②
③
把③代入①②,化简,得到一个新的二元一次方程组
解这个二元一次方程组,得
因此,
答:a=7,b=-4,c=6.
例5 某车间每天能生产甲种零件180个,或者乙种零件150个,或者丙种零件300个,甲,乙,丙3种零件分别取3个,2个,1个,才能配一套,要在30天内生产最多的成套产品,问甲,乙,丙3种零件各应生产多少天?
解:设甲种零件生产x天,乙种零件生产y天,丙种零件生产z天,根据题意,得
化简,得
解这个方程组,得
答:甲种零件生产15天,乙种零件生产12天,丙种零件生产3天.
例6? 解方程组:
解:①+②+③,得(x+y+z)2=81
∴ x+y+z=±9 ④
①÷④,得x=±1
②÷④,得y=±3
③÷④,得z=±5
∴原方程组的解为 或
x=1
y=3
z=5
x=-1
y=-3
z=-5
例7 己知x , y , z 满足方程组
求 x : y : z的值.
解:把字母z当成已知数,则原方程可变形为
解这个方程组,得
x-2y=-z
5x-4y=7z
∴x:y:z=20:13:6
解三元一次方程组的基本思路:
通过“代入”或“加减”进行消元,把“三元”化为“二元”,将三元一次方程组转化为二元一次方程组,进而转化为一元一次方程进行求解.
课堂小结
三元一次方程组
二元一次方程组
一元一次方程
消元
消元
2. 三元一次方程组 的解是
_____________.
1.已知x∶y∶z=1∶2∶3,且x+y+z=30,
则xyz=________.
750
随堂练习
3. 三元一次方程组
的解是_____________.
4.三元一次方程组 的解是__________.
5.已知 并且Z≠0,求x:y的值.
5x-4y-29z=0
X-3y+3z=0
解:把字母z当成已知数,则原方程可变形为
解这个方程组,得
5x-4y=29z
x-3y=-3z
∴x:y=9:4
x=9z
y=4z
6.己知: ,
求:(1)x : z 的值.(2)y : z 的值.
解:原方程组可化为
解此方程组,得
∴x : z=7:1.y : z=4:1.
7.解方程组
解:由①可设x=t,则y=5t,z=9t,
代入②得,3t+5t-9t=-2
∴t=2
∴ x=2, y=10,z=18
∴方程的解是
问题:甲、乙、丙三数的和是33,甲数比乙数大
2,甲数的两倍与丙数的和比乙数大24,
求这三个数.
思考:题目中有几个未知数?含有几个相等关系?
你能根据题意列出几个方程?
根据题意,列方程组:
讨论:上面方程组具有什么特点?
新课导入
8.4 三元一次方程组的解法
1.了解三元一次方程组的概念;
2.熟练掌握简单的三元一次方程组的解法;
3.能选择简便,特殊的解法解特殊的三元一次方程组;
4.掌握解三元一次方程组化三元为二元或一元的思路;
5.培养分析能力,能根据题目的特点,确定消元方法、消元对象;
6.培养计算能力、训练解题技巧.
知识与能力
教学目标
1.通过用代入消元法,加减消元法解简单的三元一次方程组的训练及选择合理,简捷的方法解方程组,培养运算能力;
2.通过三元一次方程组消元后转化为二元一次方程组,再消元转化为一元一次方程及将一些代数问题转化为方程组问题的方法的学习,培养初步运用转化思想去解决问题,发展思维能力.
过程与方法
渗透消元的思想,培养学习兴趣.
情感态度与价值观
1.用代入法或加减法解三元一次方程组;
2.进一步熟悉方程组时“消元”的基本思想和灵活运用代入法、加减法等重要方法.
针对方程组的特点,选择最好的解法.
重点
难点
教学重难点
方程组中含有三个相同的未知数,每个方程中含未知数的项的次数都是1,并且一共有三个方程,像这样的方程组叫做三元一次方程组.
知识要点
有一个三位数,已知个位上的数比十位上的数大2,十位上的数比百位上的数大3,且个位、十位、百位上的数的和为17,求这个三位数是多少?
解:设个位上的数是x、十位上的数是y、百位上的数是z,根据题意,得
x-y=2 ①
y-z=3 ②
x+y+z=17 ③
②+③,得
x+2y=20 ④
①与④组成方程组
x-y=2
x+2y=20
解这个方程组,得
x=8
y=6
把y=6代入②,得 6-z=3
所以z=3
所以,这个三元一次方程组的解是
x=8
y=6
z=3
答:这个三位数是368.
①利用代入法或加减法,消去一个未知数,得出一个二元一次方程组;
②解这个二元一次方程组,求得两个未知数的值;
③将这两个未知数的值代入原方程中较简单的一个方程,求出第三个未知数的值,把这三个数写在一起的就是所求的三元一次方程组的解.
解三元一次方程组的步骤:
例1 解三元一次方程组
3x-4y+z=11 ①
5y-z=6 ②
4x+2y-3z=12 ③
解:①×4-③×3,得
-22y+13z=8 ④
②与④组成方程组
5y-z=6
-22y+13z=8
解这个方程组,得
y=2
z=4
把y=2 ,z=4代入①,得
3x-4×2+4=11
所以 x=5
因此,三元一次方程组的解是
x=5
y=2
z=4
例2 解三元一次方程组
x+y=7 ①
y+z=9 ②
z+x=8 ③
解:①+②+③得2x+2y+2z=24
即 x+y+z=12 ④
④-①得 z=5
④-②得 x=3
④-③得 y=4
x=3
y=4
z=5
因此,三元一次方程组的解为
例3 解方程组
x:y:z=2:3:5
x+y+z=200
解:此方程组即为
3x=2y ①
3z=5y ②
x+y+z=100 ③
即:
③×3 -① - ②,得 y=75
把y=75分别代入①②,得
3x=2×75
所以x=50
3z=5×75
所以Z=125
因此,三元一次方程组的解为
x=50
y=75
z=125
例4 在等式y=ax2+bx+c中,当x=1时,y=9;当x=2时,y=26;当x=0时,y=6.求a,b,c的值.
解:根据题意,得三元一次方程组
①
②
③
把③代入①②,化简,得到一个新的二元一次方程组
解这个二元一次方程组,得
因此,
答:a=7,b=-4,c=6.
例5 某车间每天能生产甲种零件180个,或者乙种零件150个,或者丙种零件300个,甲,乙,丙3种零件分别取3个,2个,1个,才能配一套,要在30天内生产最多的成套产品,问甲,乙,丙3种零件各应生产多少天?
解:设甲种零件生产x天,乙种零件生产y天,丙种零件生产z天,根据题意,得
化简,得
解这个方程组,得
答:甲种零件生产15天,乙种零件生产12天,丙种零件生产3天.
例6? 解方程组:
解:①+②+③,得(x+y+z)2=81
∴ x+y+z=±9 ④
①÷④,得x=±1
②÷④,得y=±3
③÷④,得z=±5
∴原方程组的解为 或
x=1
y=3
z=5
x=-1
y=-3
z=-5
例7 己知x , y , z 满足方程组
求 x : y : z的值.
解:把字母z当成已知数,则原方程可变形为
解这个方程组,得
x-2y=-z
5x-4y=7z
∴x:y:z=20:13:6
解三元一次方程组的基本思路:
通过“代入”或“加减”进行消元,把“三元”化为“二元”,将三元一次方程组转化为二元一次方程组,进而转化为一元一次方程进行求解.
课堂小结
三元一次方程组
二元一次方程组
一元一次方程
消元
消元
2. 三元一次方程组 的解是
_____________.
1.已知x∶y∶z=1∶2∶3,且x+y+z=30,
则xyz=________.
750
随堂练习
3. 三元一次方程组
的解是_____________.
4.三元一次方程组 的解是__________.
5.已知 并且Z≠0,求x:y的值.
5x-4y-29z=0
X-3y+3z=0
解:把字母z当成已知数,则原方程可变形为
解这个方程组,得
5x-4y=29z
x-3y=-3z
∴x:y=9:4
x=9z
y=4z
6.己知: ,
求:(1)x : z 的值.(2)y : z 的值.
解:原方程组可化为
解此方程组,得
∴x : z=7:1.y : z=4:1.
7.解方程组
解:由①可设x=t,则y=5t,z=9t,
代入②得,3t+5t-9t=-2
∴t=2
∴ x=2, y=10,z=18
∴方程的解是
