人教版高中数学选修1-1第二章 圆锥曲线与方程2.2 双曲线探究与发现为什么y=±b/a x是双曲线的渐近线教学课件 (共15张PPT)
文档属性
| 名称 | 人教版高中数学选修1-1第二章 圆锥曲线与方程2.2 双曲线探究与发现为什么y=±b/a x是双曲线的渐近线教学课件 (共15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-02 00:00:00 | ||
图片预览




文档简介
(共15张PPT)
曲线特征:取值范围,对称性,图象走势……
创设情境,提出问题
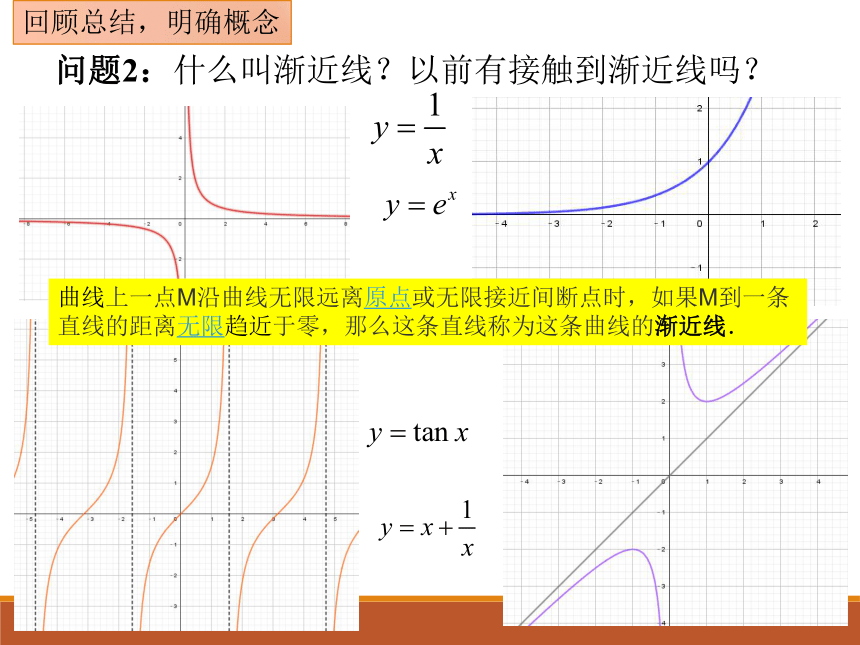
问题2:什么叫渐近线?以前有接触到渐近线吗?
曲线上一点M沿曲线无限远离原点或无限接近间断点时,如果M到一条直线的距离无限趋近于零,那么这条直线称为这条曲线的渐近线.
回顾总结,明确概念
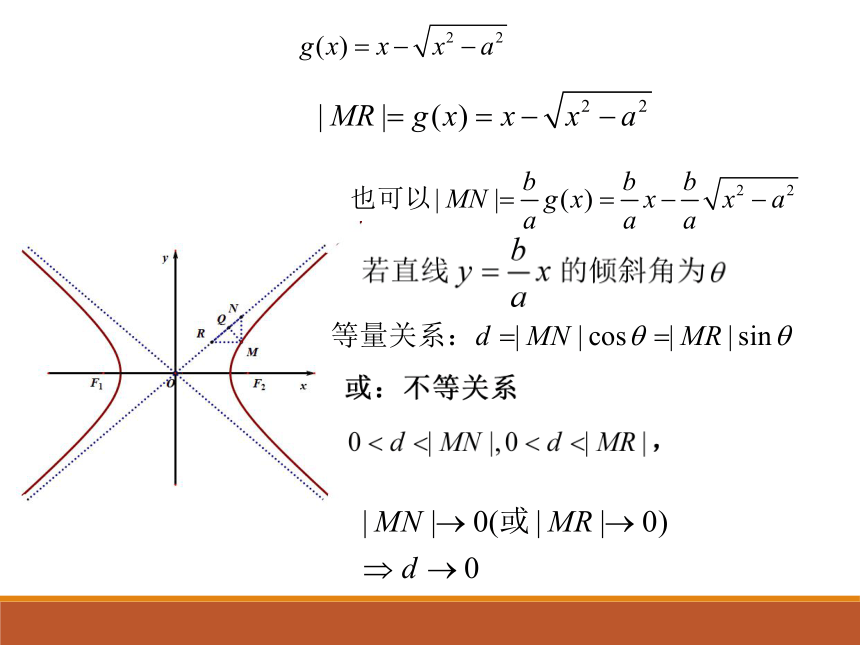
推理论证,分析问题
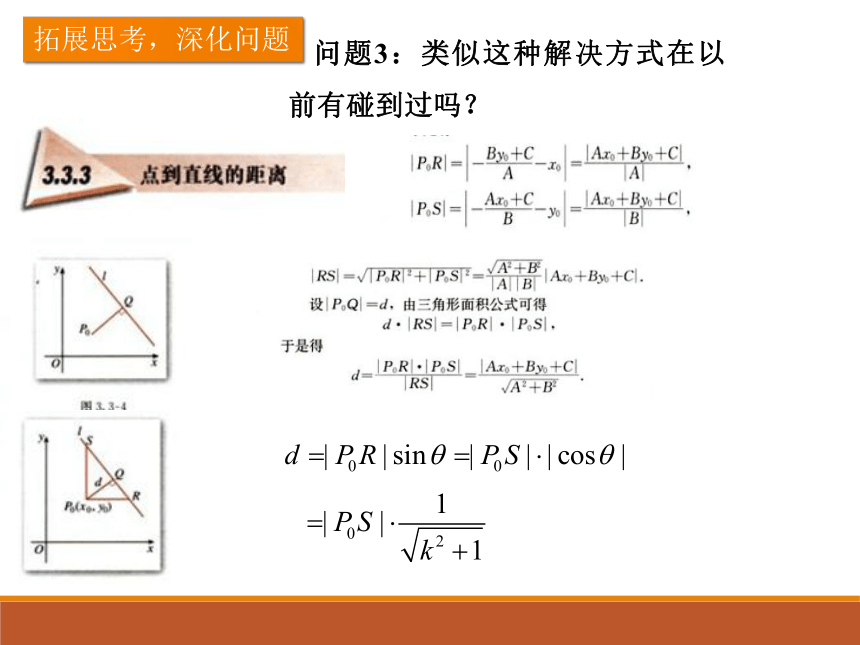
问题3:类似这种解决方式在以前有碰到过吗?
拓展思考,深化问题
应用巩固,反馈问题
拓展思考,深化问题
小结
2. 得到双曲线的渐近线方程的一种简便方法;
3.在已知渐近线的情况下,双曲线方程一种设法,即共渐近线的双曲线方程的一般形式;
过程:提出问题,分析问题,解决问题
作业
安你伤发现
F
……………
F
+8
2
8
3
2
1
1
………………………X………………
R
333点到直线的距离
如图3.3-4,已知点P(x0,y),直线l:Ax+By+C=0,如何求点
P。到直线l的距离?
图3.3-4
PlTe. Xo)
于是有
PoRI
Byo+C
AxotByo+C
A
PoS=
Axo+C
Axo+Byo+C
B
B
RS|=√PRP+PS|F=
+B
I Aro+By+C
设PQ=d,由三角形面积公式可得
d·RS|=|PR|·|PS|,
于是得
d=IPR P SI- Azo+By+CI
A+B2
333点到直线的距离
如图3.3-4,已知点P0(x,y),直线l:Ax+By+C=0,如何求点
P。到直线l的距离?
点P到直线l的距离,是指从点P到直线l的垂线段
PQ的长度,其中Q是垂足(图3.3-4)
由PQ⊥l,以及直线的斜率为一B,可得l的垂线
PQ的斜率为,垂线PQ的方程可以求出.直线PQ与
图3.3-4
直线l的交点,即垂足Q点的坐标也可以求出.于是P与
Q间的距离PQ可以求出,PQ的长即为点P到直线l
试一试,你能求出
的距离
PQ吗?
上述方法虽然思路十分自然,但具体运算较繁,下面我
们采用另一种方法
如图3.3-5,设A≠0,B≠0,则直线l与x轴和y轴都
相交,过点P分别作x轴和y轴的平行线,交直线l于R
和S,则直线PR的方程为y=y,R的坐标为
A,):直线PS的方程为x=x,S的坐标
+C
为
Aro+O
P(x,知)
于是有
I PoR=
Byo+C
Axo+Byo+Cl
Axo+C
Axo+Byo+CI
图3.3-5
I PoS=
B
B
曲线特征:取值范围,对称性,图象走势……
创设情境,提出问题
问题2:什么叫渐近线?以前有接触到渐近线吗?
曲线上一点M沿曲线无限远离原点或无限接近间断点时,如果M到一条直线的距离无限趋近于零,那么这条直线称为这条曲线的渐近线.
回顾总结,明确概念
推理论证,分析问题
问题3:类似这种解决方式在以前有碰到过吗?
拓展思考,深化问题
应用巩固,反馈问题
拓展思考,深化问题
小结
2. 得到双曲线的渐近线方程的一种简便方法;
3.在已知渐近线的情况下,双曲线方程一种设法,即共渐近线的双曲线方程的一般形式;
过程:提出问题,分析问题,解决问题
作业
安你伤发现
F
……………
F
+8
2
8
3
2
1
1
………………………X………………
R
333点到直线的距离
如图3.3-4,已知点P(x0,y),直线l:Ax+By+C=0,如何求点
P。到直线l的距离?
图3.3-4
PlTe. Xo)
于是有
PoRI
Byo+C
AxotByo+C
A
PoS=
Axo+C
Axo+Byo+C
B
B
RS|=√PRP+PS|F=
+B
I Aro+By+C
设PQ=d,由三角形面积公式可得
d·RS|=|PR|·|PS|,
于是得
d=IPR P SI- Azo+By+CI
A+B2
333点到直线的距离
如图3.3-4,已知点P0(x,y),直线l:Ax+By+C=0,如何求点
P。到直线l的距离?
点P到直线l的距离,是指从点P到直线l的垂线段
PQ的长度,其中Q是垂足(图3.3-4)
由PQ⊥l,以及直线的斜率为一B,可得l的垂线
PQ的斜率为,垂线PQ的方程可以求出.直线PQ与
图3.3-4
直线l的交点,即垂足Q点的坐标也可以求出.于是P与
Q间的距离PQ可以求出,PQ的长即为点P到直线l
试一试,你能求出
的距离
PQ吗?
上述方法虽然思路十分自然,但具体运算较繁,下面我
们采用另一种方法
如图3.3-5,设A≠0,B≠0,则直线l与x轴和y轴都
相交,过点P分别作x轴和y轴的平行线,交直线l于R
和S,则直线PR的方程为y=y,R的坐标为
A,):直线PS的方程为x=x,S的坐标
+C
为
Aro+O
P(x,知)
于是有
I PoR=
Byo+C
Axo+Byo+Cl
Axo+C
Axo+Byo+CI
图3.3-5
I PoS=
B
B
