人教版八年级数学下册 18.2.1 矩形 课件(共49张PPT)
文档属性
| 名称 | 人教版八年级数学下册 18.2.1 矩形 课件(共49张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-02 08:31:55 | ||
图片预览







文档简介
(共49张PPT)
平行四边形
有两组对边分别平行的四边形.
回顾旧知
18.2.1 矩形
平行四边形
对边相等
邻边不相等
对角相等
邻角不相等
边特殊化
角特殊化
对边相等
邻边相等
对角相等
邻角相等
四条边都相等
四个角都相等
新课导入
【知识与能力】
【过程与方法】
掌握矩形的概念和性质.
理解矩形与平行四边形的区别与联系.
理解并掌握矩形的判定方法.
会初步运用矩形的概念和性质来解决有关问题.
使学生能应用矩形定义、判定等知识,解决简单的证明题和计算题,进一步培养学生的分析能力.
教学目标
【情感态度与价值观】
渗透运动联系、从量变到质变的观点.
矩形的性质.
矩形的判定.
矩形的性质的灵活应用.
矩形的判定及性质的综合应用.
教学重难点
拿一个活动的平行四边形教具,轻轻拉动一个点,观察不管怎么拉,它还是一个平行四边形吗?为什么?
当移动到一个角是直角时停止,这是什么图形?
观 察
有一个角是直角的平行四边形叫做矩形(通常也叫长方形).
矩形
矩形是特殊的平行四边形.
∠A=90°
ABCD
即:
ABCD是矩形.
生活中的矩形
四边形
平行
四边形
两组对边
分别平行
一个角
是直角
四边形
平行四边形
矩形
矩形
矩形与四边形、平行四边形的关系
矩形有什么性质?
有平行四边形的所有性质
还有其它特殊的性质
用类比的方法探究矩形的性质,先找共性再找特殊性,并注意性质的整合.
A
B
C
D
O
矩形的对边平行且相等.
矩形的对角相等.
矩形的对角线互相平分.
矩形的一般性质(即平行四边形所有性质)
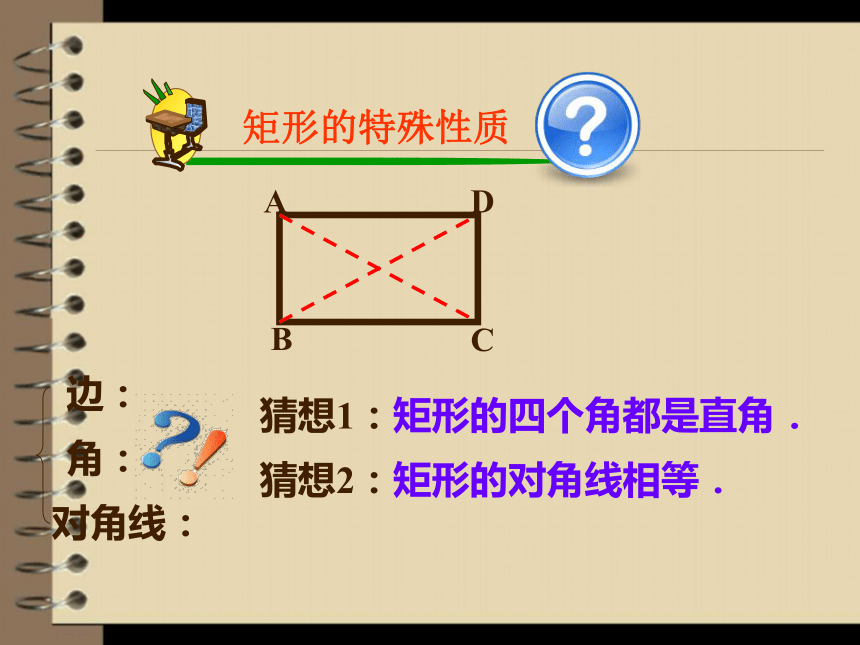
边:
角:
对角线:
猜想1:矩形的四个角都是直角.
猜想2:矩形的对角线相等.
A
B
C
D
矩形的特殊性质
角:
对角线:
边:
矩形的四个角都是直角
已知:四边形ABCD是矩形
求证:∠A=∠B=∠C=∠D=90°
D
C
B
A
证明:∵四边形ABCD是平行四边形, ∠C=90°
∴∠A=∠C=90° ∠B+∠C=180 °
∴∠B=180-∠C=90°
∴∠D=∠B=90°
即∠A=∠B=∠C=∠D=90°
探究1
定理证明
已知:四边形ABCD是矩形
求证:AC = BD
A
B
C
D
证明:在矩形ABCD中
∵∠ABC = ∠DCB = 90°
又∵AB = DC , BC = CB
∴△ABC≌△DCB(SAS)
∴AC = BD
矩形的对角线相等
探究2
定理证明
矩形的性质
A
B
C
D
知识要点
矩形的对边平行且相等.
角
对角线
边
矩形的对角线相等.
矩形的对角线互相平分.
矩形的四个角都是直角.
矩形的对角相等.
对称性
矩形是轴对称图形,
也是中心对称图形.
A
B
C
D
O
直角三角形斜边上的中线等于斜边的一半.
在Rt△ABC中, BO是斜边AC上的中线,
则BO= AC.
矩形特殊性质的推论
直角三角形的一个性质
即:
O
C
B
A
D
D
证明: 延长BO至D,使OD=BO
连结AD、DC.
∵AO=OC, BO=OD
∴四边形ABCD是平行四边形.
∵∠ABC=90°
∴ ABCD是矩形
∴AC=BD
1
2
1
2
∴BO= BD= AC
已知:在Rt△ABC中∠ABC=90°,BO是AC上的中线.
求证: BO = AC
定理证明
相等的角:
在矩形ABCD中,找出相等的线段与相等的角.
A
D
C
B
O
小练习
相等的线段:
AB=CD
AD=BC
AC=BD
OA=OC=OB
=OD= AC
= BD
∠DAB=∠ABC=∠BCD=∠CDA=90°
∠AOB=∠DOC
∠AOD=∠BOC
∠OAB=∠OBA=∠ODC=∠OCD ∠OAD=∠ODA=∠OBC=∠OCB
等腰三角形:
△OAB △ OBC △OCD △OAD
直角三角形:
Rt△ABC Rt△BCD Rt△CDA Rt△DAB
全等三角形:
Rt△ABC ≌ Rt△BCD ≌ Rt△CDA ≌ Rt△DAB
△OAB≌△OCD △OAD≌△OCB
在矩形ABCD中,找出所有等腰、直角、全等三角形.
A
D
C
B
O
小练习
矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4cm,求矩形对角线的长。
例题
解:∵ 四边形ABCD是矩形,
∴ AC与BD相等且互相平分.
∴ OA=OB。
又 ∠AOB=60°,
∴ △OAB是等边三角形.
∴ 矩形的对角线长
AC=BD = 2OA=2×4=8(cm).
矩形 ABCD,AB长8 cm ,对角线比AD边长4 cm。求AD的长及点A到BD的距离AE的长。
例题
解:设AD=xcm,则对角线长(x+4)cm,在
Rt△ABD中,由勾股定理:
解得x=6。则 AD=6cm。
“直角三角形斜边上的高”是一个基本图形,利用面积公式,可得到两直角边、斜边及斜边上的高的一个基本关系式:
AE×DB= AD×AB,解得 AE= 4.8cm.
已知:矩形ABCD中,E是BC上一点,
DF⊥AE于F,若AE=BC.
求证:CE=EF。
例题
证明:∵ 四边形ABCD是矩形
∴ ∠B=90°,且AD∥BC
∴ ∠1=∠2
∵ DF⊥AE
∴ ∠AFD=90°
∴ ∠B=∠AFD。又 AD=AE
∴ △ABE≌△DFA(AAS)
∴ AF=BE
∴ EF=EC
矩形的问题常可以转化为直角三角形或等腰三角形的问题来解决.
怎样判定一个四边形是否为矩形?
根据矩形的定义去判定.
有一个角是直角的平行四边形是矩形.
猜想1:对角线相等的平行四边形是矩形.
猜想2:有三个角是直角的四边形是矩形.
A
B
C
D
除了根据定义判定,
还有其它判定矩形的方法吗?
角:
对角线:
边:
工人师傅为了检验两组对边相等的四边形窗框是否成矩形,一种方法是量一量这个四边形的两条对角线长度,如果对角线长度相等,则窗框一定是矩形,你知道为什么吗?
猜想1:对角线相等的平行四边形是矩形.
实际问题
对角线相等的平行四边形是矩形
已知:平行四边形ABCD,AC=BD.
求证:平行四边形ABCD是矩形.
证明:
∵ AB=CD, BC=BC, AC=BD
∴ △ABC≌ △DCB(SSS)
∵ AB//CD
∴ ∠ABC+∠DCB=180°
∴ ∠ABC=∠DCB=90°
又∵ 四边形ABCD是平行四边形
∴四边形ABCD是矩形
∴ ∠ABC=∠DCB
A
D
C
B
O
探究1
定理证明
对角线相等的平行四边形是矩形 .
对角线相等且互相平分的四边形是矩形.
举一反三
对角线互相平分.
矩形的判定定理1的推论
李芳同学用画“边——直角、边——直角、边——直角、边”这样四步,画出了一个四边形,她说这就是一个矩形,她的判断对吗?为什么?
猜想2:有三个角是直角的四边形是矩形 .
实际问题
有三个角是直角的四边形是矩形.
已知:四边形ABCD,∠A=∠B=∠C = 90°
求证:四边形ABCD是矩形.
探究2
定理证明
证明:
由多边形内角和公式 (n-2)180 得,
四边形内角和= (4-2)180= 360°
∴∠D= 360°-90°-90°-90°= 90°
∵∠A+ ∠B=180° ∴AD∥BC
∵∠B+ ∠C=180° ∴AB∥CD
∴四边形ABCD是平行四边形.
又∵ ∠A = 90°
∴四边形ABCD是矩形.
A
D
B
C
判定一个四边形是矩形,知道三个角是直角,条件就够了.
因为由四边形内角和可知,这时第四个角一定是直角.
有三个角是直角的四边形是矩形.
注意
有一个角是直角的平行四边形是矩形.
对角线相等的平行四边形是矩形.
对角线相等且互相平分的四边形是矩形.
有三个角是直角的四边形是矩形.
矩形的判定定理
知识要点
脸蛋方方是矩形,例如黑板和窗门.
对角线段皆相等,相互交叉且平分.
内有直角三角形,斜边中线半斜边.
若要牢记其定义,直角平行四边形.
矩形之歌
矩形的定义:有一个角是直角的平行四边形.
矩形的性质:
矩形的判定:
具有平行四边形的一切特征.
四个角都是直角.
对角线相等的平行四边形.
对角线相等且平分.
有一个角是直角的平行四边形.
有三个角是直角的四边形.
对角线相等且平分的四边形.
课堂小结
随堂练习
1. 下列判定矩形的说法是否正确?
(1)对角线相等的四边形是矩形
(2)对角线互相平分且相等的四边形是矩形
(3)有一个角是直角的四边形是矩形
(4)有三个角都相等的四边形是矩形
√
×
×
×
(5)有三个角是直角的四边形是矩形
√
(6)四个角都相等的四边形是矩形
(7)对角线相等,且有一个角是直角的四边形是矩形
(10)一组邻边垂直,一组对边平行且相等的四
边形是矩形
(9)对角线相等且互相垂直的四边形是矩形
(8)一组对角互补的平行四边形是矩形
√
×
√
√
×
2. 填空:
(1)矩形的定义中有两个条件:一是__________ ,
二是____________________ .
(2)已知矩形的一条对角线与一边的夹角为30°,则矩形两条对角线相交所得的四个角的度数分别为____、____ 、 ____ 、 ____ 。
(3)已知矩形的一条对角线长为10cm,两条对角线的一个交角为120°,则矩形的边长分别为______ cm, ____ cm, ______ cm,____ cm。
有一个角是直角
平行四边形
60°
60°
120°
120°
5
5
3.下列说法错误的是( )
A. 矩形的对角线互相平分。
B. 矩形的对角线相等。
C. 有一个角是直角的四边形是矩形。
D. 有一个角是直角的平行四边形叫做矩形。
4. 矩形的对角线把矩形分成的三角形中全等三角形一共有( )
A. 2对 B. 4对 C. 6对 D. 8对
C
B
5. ABCD的对角线AC、BD相交于点O,△AOB是等边三角形,AB=4 cm,求这个平行四边形的面积。
解:∵四边形ABCD是平行四边形
∴AO= AC,BO= BD
∵ AO=BO
∴AC=BD
∴ ABCD是矩形(对角线相等的平行四边形是矩形)
在Rt△ABC中
∵AB=4cm,AC=2AO=8cm
∴
6. ABCD的四个内角的平分线分别相交于点E,F,G,H.求证:四边形EFGH是矩形。
证明:∵ 四边形ABCD是平行四边形
∴ AD∥BC
∴∠DAB+∠ABC=180°
又 AE平分∠DAB,BG平分∠ABC
∴∠EAB+∠ABG= ×180°=90°
∴∠AFB=90°
同理可证 ∠AED=∠BGC=∠CHD=90°
∴ 四边形EFGH是平行四边形(有三个角是
直角的四边形是矩形)
7. 工人师傅做铝合金窗框分下面三个步骤进行:
(1)先截出两对符合规格的铝合金窗料(如图1),使
AB=CD, EF=GH
(2)摆放成如图(2)的四边形,则这时窗框的形状是
_____,根据的数学道理是_________
______________
(3)将直角尺靠紧窗框的一个角(如图3)调整窗框的边
框,当直角尺的两条直角边与窗框无缝隙时(如图4)
说明窗框合格,这时窗框是____,根据的数学道理
是_______________________
B
A
C
E
D
G
F
H
1
2
3
4
平行四边形
两组对边分别相等的
矩形
有一个角是直角的平行四边形是矩形
四边形是平行四边形
8. 用8块相同的长方形地砖拼成一个矩形地面,则每块长方形地砖的长和宽分别是( )
A. 48cm,12cm B. 48cm,16cm;
C. 44cm,16cm D. 45cm,15cm.
60cm
D
9. 四个学生正在做投圈游戏,他们分别站在一个矩形的四个顶点处,目标物放在对角线的交点处,这样的队形对每个人公平吗?为什么?
O
A
B
C
D
公平,因为OA=OC=OB=OD
10. 小明想要做一个矩形像框,于是找来两根长度相等的短木条和两根长度相等的长木条制作,你有什么办法可以检测他做的是矩形像框吗?
平行四边形
有两组对边分别平行的四边形.
回顾旧知
18.2.1 矩形
平行四边形
对边相等
邻边不相等
对角相等
邻角不相等
边特殊化
角特殊化
对边相等
邻边相等
对角相等
邻角相等
四条边都相等
四个角都相等
新课导入
【知识与能力】
【过程与方法】
掌握矩形的概念和性质.
理解矩形与平行四边形的区别与联系.
理解并掌握矩形的判定方法.
会初步运用矩形的概念和性质来解决有关问题.
使学生能应用矩形定义、判定等知识,解决简单的证明题和计算题,进一步培养学生的分析能力.
教学目标
【情感态度与价值观】
渗透运动联系、从量变到质变的观点.
矩形的性质.
矩形的判定.
矩形的性质的灵活应用.
矩形的判定及性质的综合应用.
教学重难点
拿一个活动的平行四边形教具,轻轻拉动一个点,观察不管怎么拉,它还是一个平行四边形吗?为什么?
当移动到一个角是直角时停止,这是什么图形?
观 察
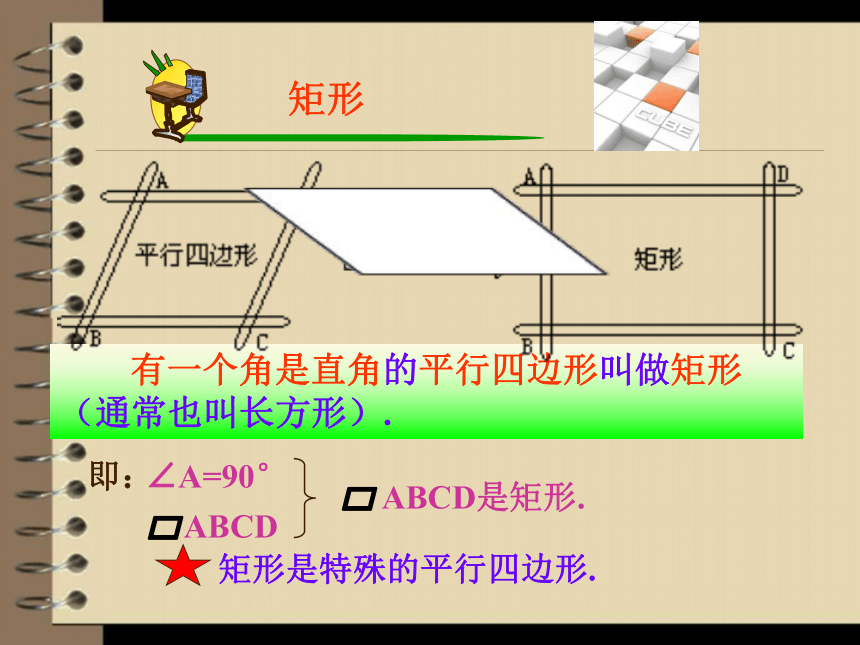
有一个角是直角的平行四边形叫做矩形(通常也叫长方形).
矩形
矩形是特殊的平行四边形.
∠A=90°
ABCD
即:
ABCD是矩形.
生活中的矩形
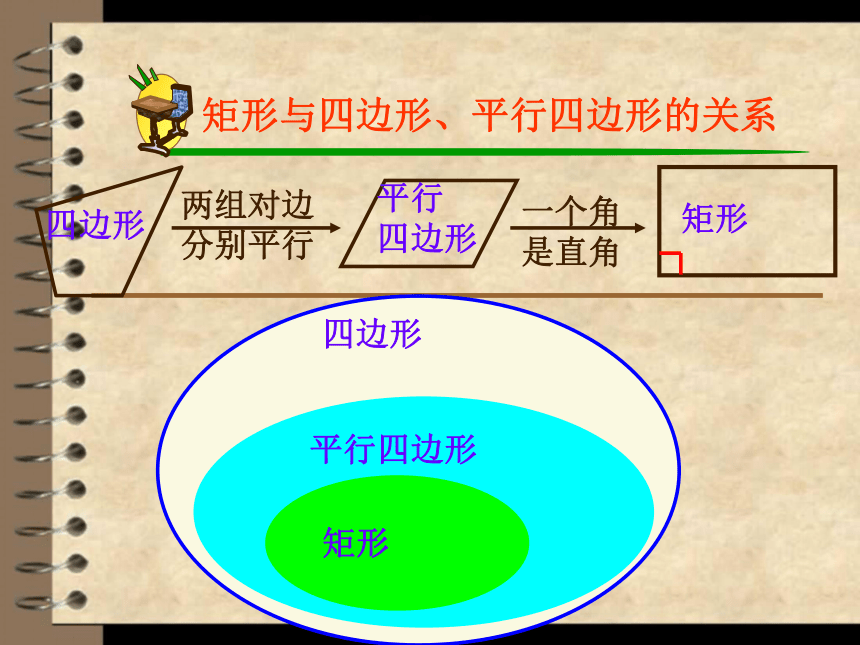
四边形
平行
四边形
两组对边
分别平行
一个角
是直角
四边形
平行四边形
矩形
矩形
矩形与四边形、平行四边形的关系
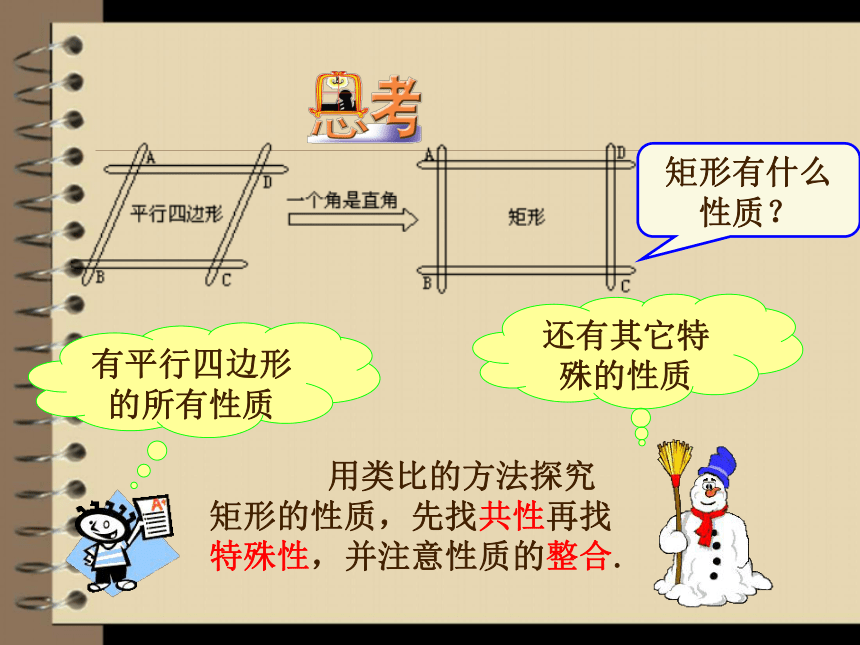
矩形有什么性质?
有平行四边形的所有性质
还有其它特殊的性质
用类比的方法探究矩形的性质,先找共性再找特殊性,并注意性质的整合.
A
B
C
D
O
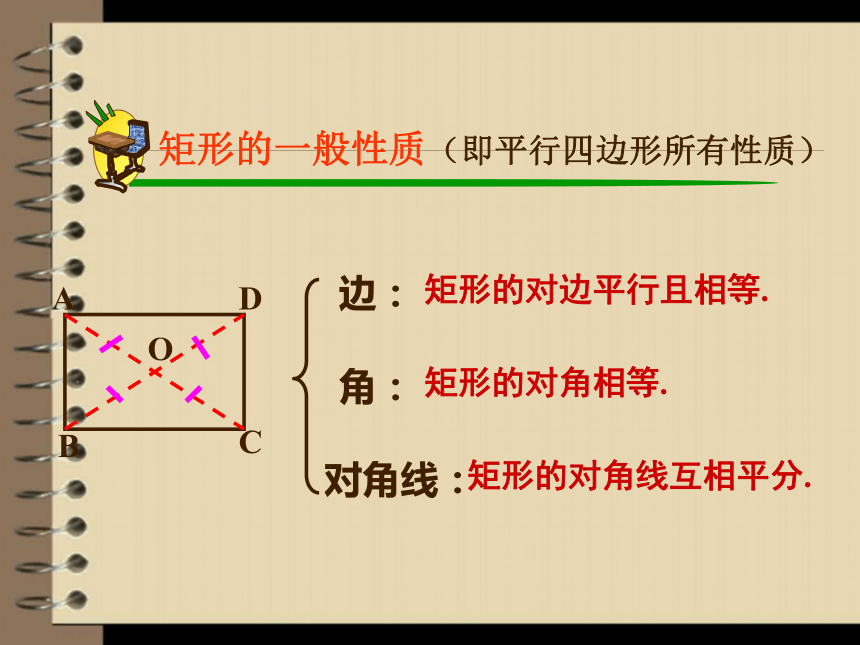
矩形的对边平行且相等.
矩形的对角相等.
矩形的对角线互相平分.
矩形的一般性质(即平行四边形所有性质)
边:
角:
对角线:
猜想1:矩形的四个角都是直角.
猜想2:矩形的对角线相等.
A
B
C
D
矩形的特殊性质
角:
对角线:
边:
矩形的四个角都是直角
已知:四边形ABCD是矩形
求证:∠A=∠B=∠C=∠D=90°
D
C
B
A
证明:∵四边形ABCD是平行四边形, ∠C=90°
∴∠A=∠C=90° ∠B+∠C=180 °
∴∠B=180-∠C=90°
∴∠D=∠B=90°
即∠A=∠B=∠C=∠D=90°
探究1
定理证明
已知:四边形ABCD是矩形
求证:AC = BD
A
B
C
D
证明:在矩形ABCD中
∵∠ABC = ∠DCB = 90°
又∵AB = DC , BC = CB
∴△ABC≌△DCB(SAS)
∴AC = BD
矩形的对角线相等
探究2
定理证明
矩形的性质
A
B
C
D
知识要点
矩形的对边平行且相等.
角
对角线
边
矩形的对角线相等.
矩形的对角线互相平分.
矩形的四个角都是直角.
矩形的对角相等.
对称性
矩形是轴对称图形,
也是中心对称图形.
A
B
C
D
O
直角三角形斜边上的中线等于斜边的一半.
在Rt△ABC中, BO是斜边AC上的中线,
则BO= AC.
矩形特殊性质的推论
直角三角形的一个性质
即:
O
C
B
A
D
D
证明: 延长BO至D,使OD=BO
连结AD、DC.
∵AO=OC, BO=OD
∴四边形ABCD是平行四边形.
∵∠ABC=90°
∴ ABCD是矩形
∴AC=BD
1
2
1
2
∴BO= BD= AC
已知:在Rt△ABC中∠ABC=90°,BO是AC上的中线.
求证: BO = AC
定理证明
相等的角:
在矩形ABCD中,找出相等的线段与相等的角.
A
D
C
B
O
小练习
相等的线段:
AB=CD
AD=BC
AC=BD
OA=OC=OB
=OD= AC
= BD
∠DAB=∠ABC=∠BCD=∠CDA=90°
∠AOB=∠DOC
∠AOD=∠BOC
∠OAB=∠OBA=∠ODC=∠OCD ∠OAD=∠ODA=∠OBC=∠OCB
等腰三角形:
△OAB △ OBC △OCD △OAD
直角三角形:
Rt△ABC Rt△BCD Rt△CDA Rt△DAB
全等三角形:
Rt△ABC ≌ Rt△BCD ≌ Rt△CDA ≌ Rt△DAB
△OAB≌△OCD △OAD≌△OCB
在矩形ABCD中,找出所有等腰、直角、全等三角形.
A
D
C
B
O
小练习
矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4cm,求矩形对角线的长。
例题
解:∵ 四边形ABCD是矩形,
∴ AC与BD相等且互相平分.
∴ OA=OB。
又 ∠AOB=60°,
∴ △OAB是等边三角形.
∴ 矩形的对角线长
AC=BD = 2OA=2×4=8(cm).
矩形 ABCD,AB长8 cm ,对角线比AD边长4 cm。求AD的长及点A到BD的距离AE的长。
例题
解:设AD=xcm,则对角线长(x+4)cm,在
Rt△ABD中,由勾股定理:
解得x=6。则 AD=6cm。
“直角三角形斜边上的高”是一个基本图形,利用面积公式,可得到两直角边、斜边及斜边上的高的一个基本关系式:
AE×DB= AD×AB,解得 AE= 4.8cm.
已知:矩形ABCD中,E是BC上一点,
DF⊥AE于F,若AE=BC.
求证:CE=EF。
例题
证明:∵ 四边形ABCD是矩形
∴ ∠B=90°,且AD∥BC
∴ ∠1=∠2
∵ DF⊥AE
∴ ∠AFD=90°
∴ ∠B=∠AFD。又 AD=AE
∴ △ABE≌△DFA(AAS)
∴ AF=BE
∴ EF=EC
矩形的问题常可以转化为直角三角形或等腰三角形的问题来解决.
怎样判定一个四边形是否为矩形?
根据矩形的定义去判定.
有一个角是直角的平行四边形是矩形.
猜想1:对角线相等的平行四边形是矩形.
猜想2:有三个角是直角的四边形是矩形.
A
B
C
D
除了根据定义判定,
还有其它判定矩形的方法吗?
角:
对角线:
边:
工人师傅为了检验两组对边相等的四边形窗框是否成矩形,一种方法是量一量这个四边形的两条对角线长度,如果对角线长度相等,则窗框一定是矩形,你知道为什么吗?
猜想1:对角线相等的平行四边形是矩形.
实际问题
对角线相等的平行四边形是矩形
已知:平行四边形ABCD,AC=BD.
求证:平行四边形ABCD是矩形.
证明:
∵ AB=CD, BC=BC, AC=BD
∴ △ABC≌ △DCB(SSS)
∵ AB//CD
∴ ∠ABC+∠DCB=180°
∴ ∠ABC=∠DCB=90°
又∵ 四边形ABCD是平行四边形
∴四边形ABCD是矩形
∴ ∠ABC=∠DCB
A
D
C
B
O
探究1
定理证明
对角线相等的平行四边形是矩形 .
对角线相等且互相平分的四边形是矩形.
举一反三
对角线互相平分.
矩形的判定定理1的推论
李芳同学用画“边——直角、边——直角、边——直角、边”这样四步,画出了一个四边形,她说这就是一个矩形,她的判断对吗?为什么?
猜想2:有三个角是直角的四边形是矩形 .
实际问题
有三个角是直角的四边形是矩形.
已知:四边形ABCD,∠A=∠B=∠C = 90°
求证:四边形ABCD是矩形.
探究2
定理证明
证明:
由多边形内角和公式 (n-2)180 得,
四边形内角和= (4-2)180= 360°
∴∠D= 360°-90°-90°-90°= 90°
∵∠A+ ∠B=180° ∴AD∥BC
∵∠B+ ∠C=180° ∴AB∥CD
∴四边形ABCD是平行四边形.
又∵ ∠A = 90°
∴四边形ABCD是矩形.
A
D
B
C
判定一个四边形是矩形,知道三个角是直角,条件就够了.
因为由四边形内角和可知,这时第四个角一定是直角.
有三个角是直角的四边形是矩形.
注意
有一个角是直角的平行四边形是矩形.
对角线相等的平行四边形是矩形.
对角线相等且互相平分的四边形是矩形.
有三个角是直角的四边形是矩形.
矩形的判定定理
知识要点
脸蛋方方是矩形,例如黑板和窗门.
对角线段皆相等,相互交叉且平分.
内有直角三角形,斜边中线半斜边.
若要牢记其定义,直角平行四边形.
矩形之歌
矩形的定义:有一个角是直角的平行四边形.
矩形的性质:
矩形的判定:
具有平行四边形的一切特征.
四个角都是直角.
对角线相等的平行四边形.
对角线相等且平分.
有一个角是直角的平行四边形.
有三个角是直角的四边形.
对角线相等且平分的四边形.
课堂小结
随堂练习
1. 下列判定矩形的说法是否正确?
(1)对角线相等的四边形是矩形
(2)对角线互相平分且相等的四边形是矩形
(3)有一个角是直角的四边形是矩形
(4)有三个角都相等的四边形是矩形
√
×
×
×
(5)有三个角是直角的四边形是矩形
√
(6)四个角都相等的四边形是矩形
(7)对角线相等,且有一个角是直角的四边形是矩形
(10)一组邻边垂直,一组对边平行且相等的四
边形是矩形
(9)对角线相等且互相垂直的四边形是矩形
(8)一组对角互补的平行四边形是矩形
√
×
√
√
×
2. 填空:
(1)矩形的定义中有两个条件:一是__________ ,
二是____________________ .
(2)已知矩形的一条对角线与一边的夹角为30°,则矩形两条对角线相交所得的四个角的度数分别为____、____ 、 ____ 、 ____ 。
(3)已知矩形的一条对角线长为10cm,两条对角线的一个交角为120°,则矩形的边长分别为______ cm, ____ cm, ______ cm,____ cm。
有一个角是直角
平行四边形
60°
60°
120°
120°
5
5
3.下列说法错误的是( )
A. 矩形的对角线互相平分。
B. 矩形的对角线相等。
C. 有一个角是直角的四边形是矩形。
D. 有一个角是直角的平行四边形叫做矩形。
4. 矩形的对角线把矩形分成的三角形中全等三角形一共有( )
A. 2对 B. 4对 C. 6对 D. 8对
C
B
5. ABCD的对角线AC、BD相交于点O,△AOB是等边三角形,AB=4 cm,求这个平行四边形的面积。
解:∵四边形ABCD是平行四边形
∴AO= AC,BO= BD
∵ AO=BO
∴AC=BD
∴ ABCD是矩形(对角线相等的平行四边形是矩形)
在Rt△ABC中
∵AB=4cm,AC=2AO=8cm
∴
6. ABCD的四个内角的平分线分别相交于点E,F,G,H.求证:四边形EFGH是矩形。
证明:∵ 四边形ABCD是平行四边形
∴ AD∥BC
∴∠DAB+∠ABC=180°
又 AE平分∠DAB,BG平分∠ABC
∴∠EAB+∠ABG= ×180°=90°
∴∠AFB=90°
同理可证 ∠AED=∠BGC=∠CHD=90°
∴ 四边形EFGH是平行四边形(有三个角是
直角的四边形是矩形)
7. 工人师傅做铝合金窗框分下面三个步骤进行:
(1)先截出两对符合规格的铝合金窗料(如图1),使
AB=CD, EF=GH
(2)摆放成如图(2)的四边形,则这时窗框的形状是
_____,根据的数学道理是_________
______________
(3)将直角尺靠紧窗框的一个角(如图3)调整窗框的边
框,当直角尺的两条直角边与窗框无缝隙时(如图4)
说明窗框合格,这时窗框是____,根据的数学道理
是_______________________
B
A
C
E
D
G
F
H
1
2
3
4
平行四边形
两组对边分别相等的
矩形
有一个角是直角的平行四边形是矩形
四边形是平行四边形
8. 用8块相同的长方形地砖拼成一个矩形地面,则每块长方形地砖的长和宽分别是( )
A. 48cm,12cm B. 48cm,16cm;
C. 44cm,16cm D. 45cm,15cm.
60cm
D
9. 四个学生正在做投圈游戏,他们分别站在一个矩形的四个顶点处,目标物放在对角线的交点处,这样的队形对每个人公平吗?为什么?
O
A
B
C
D
公平,因为OA=OC=OB=OD
10. 小明想要做一个矩形像框,于是找来两根长度相等的短木条和两根长度相等的长木条制作,你有什么办法可以检测他做的是矩形像框吗?
