人教版八年级数学下册 18.2.2 菱形 课件(共45张PPT)
文档属性
| 名称 | 人教版八年级数学下册 18.2.2 菱形 课件(共45张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-02 00:00:00 | ||
图片预览










文档简介
(共45张PPT)
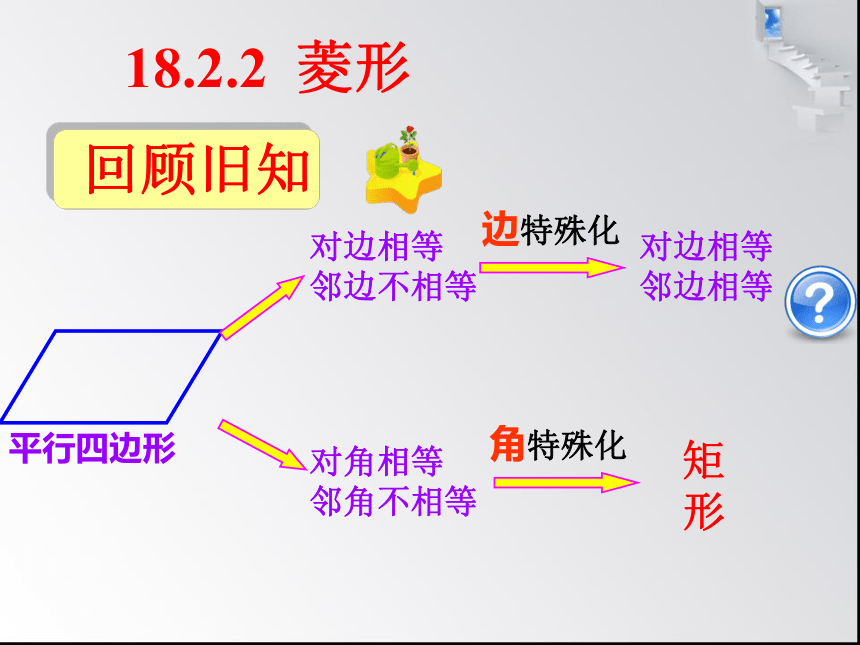
平行四边形
对边相等
邻边不相等
对角相等
邻角不相等
边特殊化
角特殊化
对边相等
邻边相等
回顾旧知
矩
形
18.2.2 菱形
掌握菱形概念.
知道菱形与平行四边形的关系.
理解并掌握菱形的定义及性质1、2.
会用这些性质进行有关的论证和计算,会计算菱形的面积.
理解并掌握菱形的定义及两个判定方法;会用这些判定方法进行有关的论证和计算。
【知识与能力】
教学目标
通过运用菱形知识解决具体问题,提高分析能力和观察能力.
在菱形的判定方法的探索与综合应用中,培养学生的观察能力、动手能力及逻辑思维能力.
【过程与方法】
【情感态度与价值观】
根据平行四边形与矩形、菱形的从属关系,通过画图向学生渗透集合思想.
菱形的性质.
菱形的性质及菱形知识的综合应用.
菱形的两个判定方法.
判定方法的证明方法及运用.
教学重难点
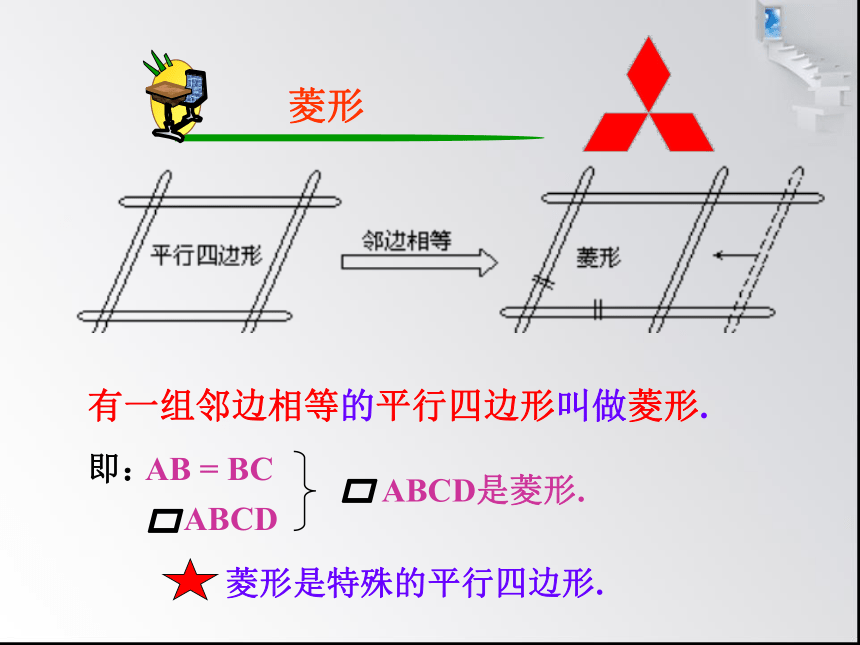
当把衣帽架拉动时,从它的形状变化,你能看出什么?
动手
有一组邻边相等的平行四边形叫做菱形.
菱形
菱形是特殊的平行四边形.
AB = BC
ABCD
ABCD是菱形.
即:
对折
对折
沿对角线裁剪
如何利用折纸、裁剪的方法,既快又准确的剪出一个菱形的纸片?
动手
生活中的菱形
飞机表演中的菱形队形
降落伞表演中的菱形
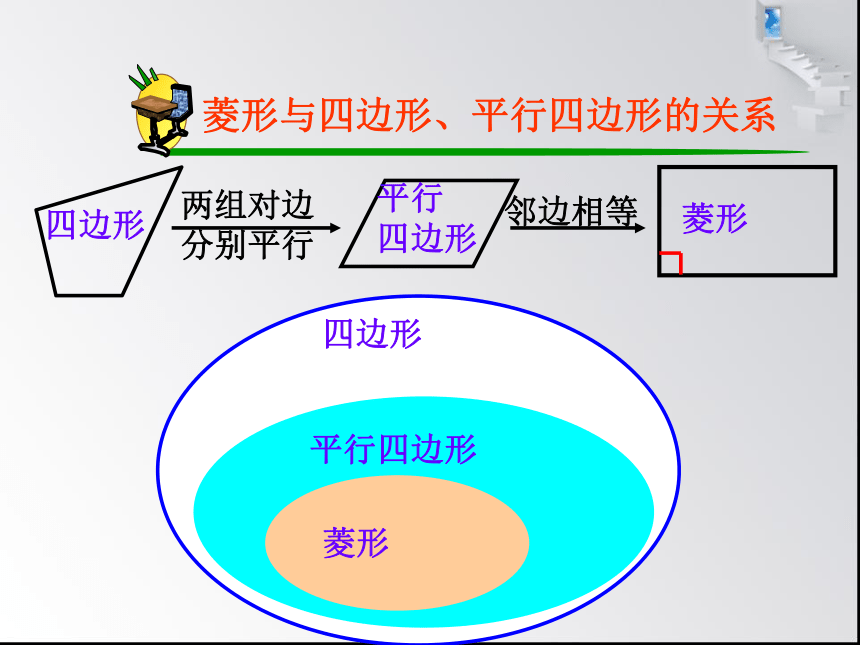
四边形
平行
四边形
两组对边
分别平行
邻边相等
四边形
平行四边形
菱形
菱形
菱形与四边形、平行四边形的关系
菱形有什么性质?
有平行四边形的所有性质
还有其它特殊的性质
用类比的方法探究菱形的性质,先找共性再找特殊性,并注意性质的整合.
菱形的对边平行且相等.
菱形的对角相等.
菱形的对角线互相平分.
菱形的一般性质(即平行四边形所有性质)
边:
角:
对角线:
A
D
C
B
猜想1:菱形的四条边都相等.
猜想2:菱形的对角线互相垂直.
菱形的特殊性质
角:
对角线:
边:
A
D
C
B
菱形是轴对称图形,也是中心对称图形.
对称轴
菱形的四条边都相等.
探究1
A
D
C
B
已知:四边形ABCD是菱形
求证:AB=BC=CD=AD
证明:∵四边形ABCD是菱形
∴AB=BC(菱形的定义)
四边形ABCD是平行四边形
∴AB=CD,BC=AD(平行四边形定义)
∴AB=BC=CD=AD
定理证明
证明:∵四边形ABCD是菱形
A
B
C
D
O
在△ABO和△ADO中,BO=DO
∴ △ABO ≌△ADO
∴AB=AD(菱形的四条边都相等)
∴AC⊥BD,AC平分∠BAD
同理: AC平分∠BCD
BD平分∠ABC和∠ADC
已知:菱形ABCD的对角线AC和BD相交于点O
求证:AC⊥BD ;
AC平分∠BAD和∠BCD
BD平分∠ABC和∠ADC
菱形的对角线互相垂直
探究2
定理证明
并且每一条对角线平分一组对角.
菱形的性质
知识要点
角
对角线
边
菱形的对角线互相垂直平分.
菱形的每一条对角线平分一组对角.
菱形的对角相等.
菱形的对边平行.
菱形的四条边相等.
A
B
C
D
O
菱形是轴对称图形,
也是中心对称图形.
对称性
在菱形ABCD中,找出相等的线段与相等的角.
小练习
相等的线段:
AB=CD=AD=BC
OA=OC OB=OD
相等的角:
∠DAB=∠BCD ∠ABC =∠CDA
∠AOB=∠DOC=∠AOD=∠BOC =90°
∠1=∠2=∠3=∠4 ∠5=∠6=∠7=∠8
A
B
C
D
O
1
2
3
4
5
6
7
8
等腰三角形:
直角三角形:
全等三角形:
△ABC △ DBC △ACD △ABD
Rt△AOB Rt△BOC Rt△COD Rt△DOA
Rt△AOB ≌ Rt△BOC≌ Rt△COD ≌ Rt△DOA
△ABD≌△BCD △ABC≌△ACD
在菱形ABCD中,找出所有等腰、直角、全等三角形.
小练习
A
B
C
D
O
1
2
3
4
5
6
7
8
S菱形 = S△ABD+S△BCD = BD×AO + BD×CO
= BD×(AO+CO)= BD×AC
菱形的面积公式
A
B
C
D
O
E
S菱形= 底×高
= BC · AE
菱形的对角线互相垂直
利用
的特殊性质.
菱形面积的其它公式?
一题多解
S菱形 = 对角线乘积的一半 = BD×AC
已知:四边形ABCD是菱形,F是AB上一点,
DF交AC于E。
求证:∠AFD=∠CBE。
例题
证明:∵四边形ABCD是菱形
∴CB=CD, CA平分∠BCD
∴∠BCE=∠DCE
又 CE=CE
∴△BCE≌△COB(SAS)
∴∠CBE=∠CDE
∵在菱形ABCD中,AB∥CD
∴∠AFD=∠FDC
∴∠AFD=∠CBE
怎样判定一个四边形是否为菱形?
根据菱形的定义去判定.
有一组邻边相等的平行四边形是菱形.
猜想1:对角线互相垂直的平行四边形是菱形.
猜想2:四边相等的四边形是菱形.
除了根据定义判定,
还有其它判定菱形的方法吗?
角:
对角线:
边:
A
B
C
D
O
对角线互相垂直的平行四边形是菱形.
A
B
C
D
O
已知: 中,AC ⊥ BD
ABCD
求证: 是菱形
ABCD
探究1
定理证明
证明:∵四边形ABCD是平行四边形
∴AO=OC
∵AC ⊥ BD ∴∠AOB=∠COB=90°
又∵BO是公共边
∴△AOB≌△COB
∴AB=BC
对角线互相垂直平分的四边形是菱形.
举一反三
对角线互相平分.
菱形的判定定理1的推论
对角线互相垂直的平行四边形是菱形.
a
B
C
A
D
3.分别以A、C为圆心,a长
为半径画弧,两弧交于点D,
连结AD、CD
1.作∠ B =∠
2.在∠B的两边上分别截取
AB=BC=a
作法:
∴四边形ABCD就是所作的菱形.
实际问题
已知:线段a
求作:一个菱形ABCD,使AB=a,∠ABC=∠
猜想2:四边都相等的四边形是菱形.
已知:四边形ABCD中,AB=BC=CD=DA
求证:四边形ABCD是菱形
四边都相等的四边形是菱形.
A
B
C
D
O
探究2
定理证明
证明:在四边形ABCD中
∵AB=CD,BC=AD
∴四边形ABCD是平行四边形
∵AB=BC
∴平行四边形ABCD是菱形
有一组邻边相等的平行四边形是菱形.
对角线互相垂直的平行四边形是菱形.
对角线互相垂直平分的四边形是菱形.
四边都相等的四边形是菱形.
菱形的判定定理
知识要点
已知: ABCD的对角线AC、BD交于点O,AB=5,AO=4,BD=3,
求证: ABCD是菱形.
A
B
C
D
O
例题
证明:∵AB=5,AO=4,BO=3
∴
∴△ABO是直角三角形
∴AC⊥BD
∴ ABCD是菱形
A
B
C
D
O
已知: ABCD的对角线AC的垂直平分线与边
AD、BC分别交于E、F.
求证:四边形AFCE是菱形.
例题
证明:∵四边形ABCD是平行四边形
∴AE∥FC
∴∠1=∠2
又∠AOE=∠COF,AO=CO
∴△AOE≌△COF
∴EO=FO
∴四边形AFCE是平行四边形
又EF⊥AC
∴AFCE是菱形(对角线互相垂直的平行四边形是菱形)
已知:△ABC中, ∠ACB=90°,BE平分
∠ABC,CD⊥AB与D,EH⊥AB于H,CD
交BE于F.
求证:四边形CEHF为菱形.
例题
证明:可证CF∥EH,CE=EH
在Rt△BCE中,∠CBE+∠CEB=90°
在Rt△BDF中,∠DBF+∠DFB=90°
∵∠CBE=∠DBF,∠CFE=∠DFB
∴∠CEB=∠CFE
∴CE=CF
∴CF=CE=EH,CF∥EH
∴四边形CEHF为菱形
课堂小结
菱形的定义:有一组邻边相等的平行四边形叫菱形.
菱形的性质:
菱形的判定:
具有平行四边形的一切特征.
四条边都相等.
对角线互相垂直的平行四边形.
菱形的对角线互相垂直,并且每一条对角线平分一组对角.
有一组邻边相等的平行四边形是菱形.
四边相等的四边形.
对角线互相垂直平分的四边形.
1. 填空:
(1)对角线互相平分的四边形是___________
(2)对角线互相垂直平分的四边形是_______
(3)对角线相等且互相平分的四边形_______
(4)两组对边分别平行,且对角线___________的
四边形是菱形
菱形
平行四边形
矩形
互相垂直
随堂练习
(5)若菱形的边长等于一条对角线的长,则
它的一组邻角的度数分别为______________.
60°和120°
2. 在菱形ABCD中,AE⊥BC,AF⊥CD,E、F分别为BC,CD的中点,那么∠EAF的度数是( )
A.75°B.60°C.45°D.30°
B
A
D
C
B
∟
∟
E
F
3. 把两张等宽的纸条交叉重叠在一起,你能判断重叠部分ABCD的形状吗?
4. 已知:菱形ABCD中,E、F分别是CB、CD上的
点,且BE=DF.
求证:∠AEF=∠AFE.
5. 已知:O是矩形ABCD的对角线的交点,
DE∥AC,CE∥BD,DE和CE相交于E.
求证:四边形OCED是菱形。
方法一:
6. 用一张长为20cm宽为15cm的矩形纸片剪菱形纸片,问怎样剪,剪出的菱形面积最大?
方法二:
方法三:
平行四边形
对边相等
邻边不相等
对角相等
邻角不相等
边特殊化
角特殊化
对边相等
邻边相等
回顾旧知
矩
形
18.2.2 菱形
掌握菱形概念.
知道菱形与平行四边形的关系.
理解并掌握菱形的定义及性质1、2.
会用这些性质进行有关的论证和计算,会计算菱形的面积.
理解并掌握菱形的定义及两个判定方法;会用这些判定方法进行有关的论证和计算。
【知识与能力】
教学目标
通过运用菱形知识解决具体问题,提高分析能力和观察能力.
在菱形的判定方法的探索与综合应用中,培养学生的观察能力、动手能力及逻辑思维能力.
【过程与方法】
【情感态度与价值观】
根据平行四边形与矩形、菱形的从属关系,通过画图向学生渗透集合思想.
菱形的性质.
菱形的性质及菱形知识的综合应用.
菱形的两个判定方法.
判定方法的证明方法及运用.
教学重难点
当把衣帽架拉动时,从它的形状变化,你能看出什么?
动手
有一组邻边相等的平行四边形叫做菱形.
菱形
菱形是特殊的平行四边形.
AB = BC
ABCD
ABCD是菱形.
即:
对折
对折
沿对角线裁剪
如何利用折纸、裁剪的方法,既快又准确的剪出一个菱形的纸片?
动手
生活中的菱形
飞机表演中的菱形队形
降落伞表演中的菱形
四边形
平行
四边形
两组对边
分别平行
邻边相等
四边形
平行四边形
菱形
菱形
菱形与四边形、平行四边形的关系
菱形有什么性质?
有平行四边形的所有性质
还有其它特殊的性质
用类比的方法探究菱形的性质,先找共性再找特殊性,并注意性质的整合.
菱形的对边平行且相等.
菱形的对角相等.
菱形的对角线互相平分.
菱形的一般性质(即平行四边形所有性质)
边:
角:
对角线:
A
D
C
B
猜想1:菱形的四条边都相等.
猜想2:菱形的对角线互相垂直.
菱形的特殊性质
角:
对角线:
边:
A
D
C
B
菱形是轴对称图形,也是中心对称图形.
对称轴
菱形的四条边都相等.
探究1
A
D
C
B
已知:四边形ABCD是菱形
求证:AB=BC=CD=AD
证明:∵四边形ABCD是菱形
∴AB=BC(菱形的定义)
四边形ABCD是平行四边形
∴AB=CD,BC=AD(平行四边形定义)
∴AB=BC=CD=AD
定理证明
证明:∵四边形ABCD是菱形
A
B
C
D
O
在△ABO和△ADO中,BO=DO
∴ △ABO ≌△ADO
∴AB=AD(菱形的四条边都相等)
∴AC⊥BD,AC平分∠BAD
同理: AC平分∠BCD
BD平分∠ABC和∠ADC
已知:菱形ABCD的对角线AC和BD相交于点O
求证:AC⊥BD ;
AC平分∠BAD和∠BCD
BD平分∠ABC和∠ADC
菱形的对角线互相垂直
探究2
定理证明
并且每一条对角线平分一组对角.
菱形的性质
知识要点
角
对角线
边
菱形的对角线互相垂直平分.
菱形的每一条对角线平分一组对角.
菱形的对角相等.
菱形的对边平行.
菱形的四条边相等.
A
B
C
D
O
菱形是轴对称图形,
也是中心对称图形.
对称性
在菱形ABCD中,找出相等的线段与相等的角.
小练习
相等的线段:
AB=CD=AD=BC
OA=OC OB=OD
相等的角:
∠DAB=∠BCD ∠ABC =∠CDA
∠AOB=∠DOC=∠AOD=∠BOC =90°
∠1=∠2=∠3=∠4 ∠5=∠6=∠7=∠8
A
B
C
D
O
1
2
3
4
5
6
7
8
等腰三角形:
直角三角形:
全等三角形:
△ABC △ DBC △ACD △ABD
Rt△AOB Rt△BOC Rt△COD Rt△DOA
Rt△AOB ≌ Rt△BOC≌ Rt△COD ≌ Rt△DOA
△ABD≌△BCD △ABC≌△ACD
在菱形ABCD中,找出所有等腰、直角、全等三角形.
小练习
A
B
C
D
O
1
2
3
4
5
6
7
8
S菱形 = S△ABD+S△BCD = BD×AO + BD×CO
= BD×(AO+CO)= BD×AC
菱形的面积公式
A
B
C
D
O
E
S菱形= 底×高
= BC · AE
菱形的对角线互相垂直
利用
的特殊性质.
菱形面积的其它公式?
一题多解
S菱形 = 对角线乘积的一半 = BD×AC
已知:四边形ABCD是菱形,F是AB上一点,
DF交AC于E。
求证:∠AFD=∠CBE。
例题
证明:∵四边形ABCD是菱形
∴CB=CD, CA平分∠BCD
∴∠BCE=∠DCE
又 CE=CE
∴△BCE≌△COB(SAS)
∴∠CBE=∠CDE
∵在菱形ABCD中,AB∥CD
∴∠AFD=∠FDC
∴∠AFD=∠CBE
怎样判定一个四边形是否为菱形?
根据菱形的定义去判定.
有一组邻边相等的平行四边形是菱形.
猜想1:对角线互相垂直的平行四边形是菱形.
猜想2:四边相等的四边形是菱形.
除了根据定义判定,
还有其它判定菱形的方法吗?
角:
对角线:
边:
A
B
C
D
O
对角线互相垂直的平行四边形是菱形.
A
B
C
D
O
已知: 中,AC ⊥ BD
ABCD
求证: 是菱形
ABCD
探究1
定理证明
证明:∵四边形ABCD是平行四边形
∴AO=OC
∵AC ⊥ BD ∴∠AOB=∠COB=90°
又∵BO是公共边
∴△AOB≌△COB
∴AB=BC
对角线互相垂直平分的四边形是菱形.
举一反三
对角线互相平分.
菱形的判定定理1的推论
对角线互相垂直的平行四边形是菱形.
a
B
C
A
D
3.分别以A、C为圆心,a长
为半径画弧,两弧交于点D,
连结AD、CD
1.作∠ B =∠
2.在∠B的两边上分别截取
AB=BC=a
作法:
∴四边形ABCD就是所作的菱形.
实际问题
已知:线段a
求作:一个菱形ABCD,使AB=a,∠ABC=∠
猜想2:四边都相等的四边形是菱形.
已知:四边形ABCD中,AB=BC=CD=DA
求证:四边形ABCD是菱形
四边都相等的四边形是菱形.
A
B
C
D
O
探究2
定理证明
证明:在四边形ABCD中
∵AB=CD,BC=AD
∴四边形ABCD是平行四边形
∵AB=BC
∴平行四边形ABCD是菱形
有一组邻边相等的平行四边形是菱形.
对角线互相垂直的平行四边形是菱形.
对角线互相垂直平分的四边形是菱形.
四边都相等的四边形是菱形.
菱形的判定定理
知识要点
已知: ABCD的对角线AC、BD交于点O,AB=5,AO=4,BD=3,
求证: ABCD是菱形.
A
B
C
D
O
例题
证明:∵AB=5,AO=4,BO=3
∴
∴△ABO是直角三角形
∴AC⊥BD
∴ ABCD是菱形
A
B
C
D
O
已知: ABCD的对角线AC的垂直平分线与边
AD、BC分别交于E、F.
求证:四边形AFCE是菱形.
例题
证明:∵四边形ABCD是平行四边形
∴AE∥FC
∴∠1=∠2
又∠AOE=∠COF,AO=CO
∴△AOE≌△COF
∴EO=FO
∴四边形AFCE是平行四边形
又EF⊥AC
∴AFCE是菱形(对角线互相垂直的平行四边形是菱形)
已知:△ABC中, ∠ACB=90°,BE平分
∠ABC,CD⊥AB与D,EH⊥AB于H,CD
交BE于F.
求证:四边形CEHF为菱形.
例题
证明:可证CF∥EH,CE=EH
在Rt△BCE中,∠CBE+∠CEB=90°
在Rt△BDF中,∠DBF+∠DFB=90°
∵∠CBE=∠DBF,∠CFE=∠DFB
∴∠CEB=∠CFE
∴CE=CF
∴CF=CE=EH,CF∥EH
∴四边形CEHF为菱形
课堂小结
菱形的定义:有一组邻边相等的平行四边形叫菱形.
菱形的性质:
菱形的判定:
具有平行四边形的一切特征.
四条边都相等.
对角线互相垂直的平行四边形.
菱形的对角线互相垂直,并且每一条对角线平分一组对角.
有一组邻边相等的平行四边形是菱形.
四边相等的四边形.
对角线互相垂直平分的四边形.
1. 填空:
(1)对角线互相平分的四边形是___________
(2)对角线互相垂直平分的四边形是_______
(3)对角线相等且互相平分的四边形_______
(4)两组对边分别平行,且对角线___________的
四边形是菱形
菱形
平行四边形
矩形
互相垂直
随堂练习
(5)若菱形的边长等于一条对角线的长,则
它的一组邻角的度数分别为______________.
60°和120°
2. 在菱形ABCD中,AE⊥BC,AF⊥CD,E、F分别为BC,CD的中点,那么∠EAF的度数是( )
A.75°B.60°C.45°D.30°
B
A
D
C
B
∟
∟
E
F
3. 把两张等宽的纸条交叉重叠在一起,你能判断重叠部分ABCD的形状吗?
4. 已知:菱形ABCD中,E、F分别是CB、CD上的
点,且BE=DF.
求证:∠AEF=∠AFE.
5. 已知:O是矩形ABCD的对角线的交点,
DE∥AC,CE∥BD,DE和CE相交于E.
求证:四边形OCED是菱形。
方法一:
6. 用一张长为20cm宽为15cm的矩形纸片剪菱形纸片,问怎样剪,剪出的菱形面积最大?
方法二:
方法三:
