人教A版高中数学必修4-2.1 平面向量的实际背景及基本概念- 课件(共25张PPT)
文档属性
| 名称 | 人教A版高中数学必修4-2.1 平面向量的实际背景及基本概念- 课件(共25张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-02 21:33:18 | ||
图片预览







文档简介
(共25张PPT)
平面向量的实际背景
及基本概念
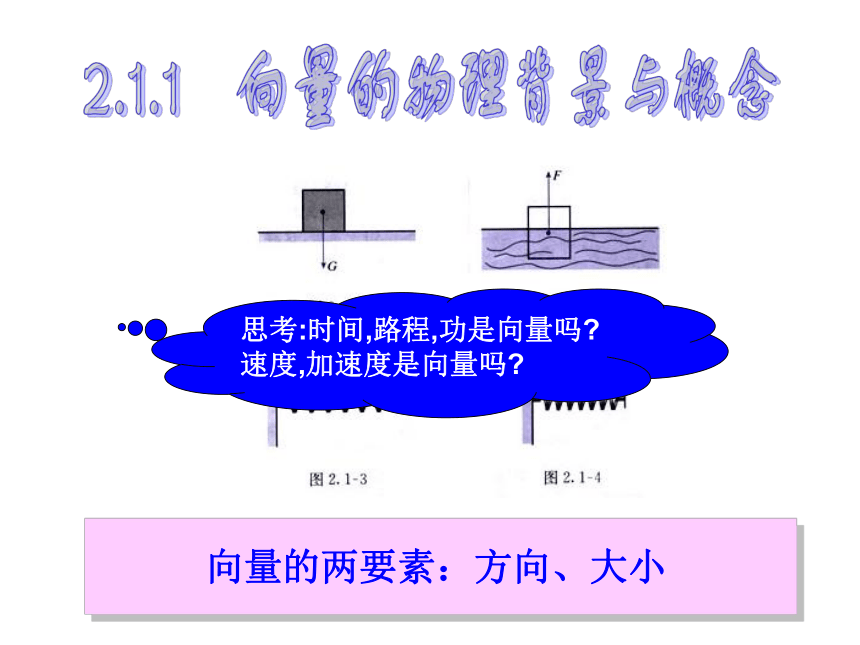
2.1.1 向量的物理背景与概念
2.1.2 向量的几何表示
2.1.3 相等向量与共线向量
阅读教材P74-76回答以下问题
1.向量与数量有何区别?请列举一些你熟悉的向量。
2.如何表示向量?
3.有哪些特殊的向量?
4.有一组向量,它们的方向相同或相反,这组向量有什么关系?
5.满足什么条件的两个向量是相等向量?单位向量是相等向量吗?
向量:既有大小,又有方向的量。
数量:只有大小,没有方向的量。
思考:时间,路程,功是向量吗?速度,加速度是向量吗?
向量的两要素:方向、大小
阅读教材P74-76回答以下问题
1.向量与数量有何区别?请列举一些你熟悉的向量。
2.如何表示向量?
3.有哪些特殊的向量?
4.有一组向量,它们的方向相同或相反,这组向量有什么关系?
5.满足什么条件的两个向量是相等向量?单位向量是相等向量吗?
1.向量的定义: 既有大小又有方向的量叫向量。
2.向量的表示:
①几何法: 用有向线段表示(有向线段具有起点、方向、长度)
如 或
②代数法: 用字母表示, 如AB或a
a
B
A
阅读教材P74-76回答以下问题
1.向量与数量有何区别?请列举一些你熟悉的向量。
2.如何表示向量?
3.有哪些特殊的向量?
4.有一组向量,它们的方向相同或相反,这组向量有什么关系?
5.满足什么条件的两个向量是相等向量?单位向量是相等向量吗?
3.向量的模: 也就是向量的长度, 如向量AB的模, 记作|AB|
4.两个基本向量:
①零向量: 长度为零的向量(方向任意), 记作0;
②单位向量: 长度等于1个单位的向量。
1.温度含零上和零下温度,所以温度是向量( )
知识点应用
×
×
2.向量的模是一个正实数。( )
×
注:向量不能比较大小
长度相等且方向相同的两个向量表示相等向量,
但是两个向量之间只有相等关系,没有大小之分,“对于向量 , , > ,或 < ”这种说法是错误的.
3.若|a|>|b| ,则a > b
( )
阅读教材P74-76回答以下问题
1.向量与数量有何区别?请列举一些你熟悉的向量。
2.如何表示向量?
3.有哪些特殊的向量?
4.有一组向量,它们的方向相同或相反,这组向量有什么关系?
5.满足什么条件的两个向量是相等向量?单位向量是相等向量吗?
平行向量又叫做共线向量
各向量的终点与直线l之间有什么关系?
如:
a
b
c
(1)平行向量:方向相同或相反的非零向量叫做平行向量。
记作 a ∥b ∥c
规定:0与任一向量平行。
问:把一组平行于直线l的向量的起点平移到直线l上的 一点O ,这时它们是不是平行向量?
o
l
.
C
OC = c
A
OA = a
OB = b
B
知识应用:判断下列各组向量是否平行?
A
B
C
A
B
C
①
④
③
②
向量的平行与线段的平行有什么区别?
阅读教材P74-76回答以下问题
1.向量与数量有何区别?请列举一些你熟悉的向量。
2.如何表示向量?
3.有哪些特殊的向量?
4.有一组向量,它们的方向相同或相反,这组向量有什么关系?
5.满足什么条件的两个向量是相等向量?单位向量是相等向量吗?
向量相等 向量平行
平行向量一定是相等向量吗?
?
相等向量一定是平行向量吗?
(2)相等向量:长度相等且方向相同的向量叫做相等向量。
记作:a = b
规定:0 = 0
a
b
o
.
b
a
11个
例1.如图设O是正六边形ABCDEF的中心,写出图中
与向量OA相等的向量。
OA = DO = CB
变式一:与向量OA长度相等的向量
有多少个?
变式二:是否存在与向量OA长度相等,方向
相反的向量?
存在,为 FE
CB、DO、FE
变式三:与向量OA长度相等的共线向量有哪些?
例2.(1)如图, 四边形ABCD和ABDE都是平行四边形。
①与向量ED相等的向量有_______;
②若|AB|=3, 则|EC|=___________
A
E
D
C
B
(2)如图, 在2×4的方格纸中, 小方格的长度为1, 则图中与 a 相等的向量有_____个。
a
习题讲解
1.判断下列命题是否正确,若不正确,请简述理由. [来源:学科网ZXXK]
?
①向量 与 是共线向量,则A、B、C、D 四点必在一直线上;
②单位向量都相等;
③任一向量与它的相反向量(长度相同,方向相反的向量)不相等;
?
④共线的向量,若起点不同,则终点一定不同。
(×)
(×)
(×)
(×)
2.下面几个命题:
C
(3)若|a|=|b|,则a = b
(2)若|a|=0,则a = 0
|a|=|b|
a ∥ b
(4)两个向量a、b相等的充要条件是
(1)若a = b,b = c,则a = c。
当b ≠ 0时成立。
变:若 a ∥ b, b ∥ c, 则a ∥c
A.0 B. 1 C. 2 D. 3
其中正确的个数是( )
(5)若A、B、C、D是不共线的四点,则AB=DC是
四边形ABCD是平形四边形的充要条件。
A
B
D
C
B
A
C
D
习题讲解
巩
固
提
高
相同
相等
B
归纳小结
零向量、单位向量概念:
向量的概念:
向量的表示方法:
共线向量与平行向量关系:
平行向量定义:
相等向量定义:
课本 第77页习题2.1组 第2,3,5题
学海导航第37页
预习下一节
课后作业
平面向量的实际背景
及基本概念
2.1.1 向量的物理背景与概念
2.1.2 向量的几何表示
2.1.3 相等向量与共线向量
阅读教材P74-76回答以下问题
1.向量与数量有何区别?请列举一些你熟悉的向量。
2.如何表示向量?
3.有哪些特殊的向量?
4.有一组向量,它们的方向相同或相反,这组向量有什么关系?
5.满足什么条件的两个向量是相等向量?单位向量是相等向量吗?
向量:既有大小,又有方向的量。
数量:只有大小,没有方向的量。
思考:时间,路程,功是向量吗?速度,加速度是向量吗?
向量的两要素:方向、大小
阅读教材P74-76回答以下问题
1.向量与数量有何区别?请列举一些你熟悉的向量。
2.如何表示向量?
3.有哪些特殊的向量?
4.有一组向量,它们的方向相同或相反,这组向量有什么关系?
5.满足什么条件的两个向量是相等向量?单位向量是相等向量吗?
1.向量的定义: 既有大小又有方向的量叫向量。
2.向量的表示:
①几何法: 用有向线段表示(有向线段具有起点、方向、长度)
如 或
②代数法: 用字母表示, 如AB或a
a
B
A
阅读教材P74-76回答以下问题
1.向量与数量有何区别?请列举一些你熟悉的向量。
2.如何表示向量?
3.有哪些特殊的向量?
4.有一组向量,它们的方向相同或相反,这组向量有什么关系?
5.满足什么条件的两个向量是相等向量?单位向量是相等向量吗?
3.向量的模: 也就是向量的长度, 如向量AB的模, 记作|AB|
4.两个基本向量:
①零向量: 长度为零的向量(方向任意), 记作0;
②单位向量: 长度等于1个单位的向量。
1.温度含零上和零下温度,所以温度是向量( )
知识点应用
×
×
2.向量的模是一个正实数。( )
×
注:向量不能比较大小
长度相等且方向相同的两个向量表示相等向量,
但是两个向量之间只有相等关系,没有大小之分,“对于向量 , , > ,或 < ”这种说法是错误的.
3.若|a|>|b| ,则a > b
( )
阅读教材P74-76回答以下问题
1.向量与数量有何区别?请列举一些你熟悉的向量。
2.如何表示向量?
3.有哪些特殊的向量?
4.有一组向量,它们的方向相同或相反,这组向量有什么关系?
5.满足什么条件的两个向量是相等向量?单位向量是相等向量吗?
平行向量又叫做共线向量
各向量的终点与直线l之间有什么关系?
如:
a
b
c
(1)平行向量:方向相同或相反的非零向量叫做平行向量。
记作 a ∥b ∥c
规定:0与任一向量平行。
问:把一组平行于直线l的向量的起点平移到直线l上的 一点O ,这时它们是不是平行向量?
o
l
.
C
OC = c
A
OA = a
OB = b
B
知识应用:判断下列各组向量是否平行?
A
B
C
A
B
C
①
④
③
②
向量的平行与线段的平行有什么区别?
阅读教材P74-76回答以下问题
1.向量与数量有何区别?请列举一些你熟悉的向量。
2.如何表示向量?
3.有哪些特殊的向量?
4.有一组向量,它们的方向相同或相反,这组向量有什么关系?
5.满足什么条件的两个向量是相等向量?单位向量是相等向量吗?
向量相等 向量平行
平行向量一定是相等向量吗?
?
相等向量一定是平行向量吗?
(2)相等向量:长度相等且方向相同的向量叫做相等向量。
记作:a = b
规定:0 = 0
a
b
o
.
b
a
11个
例1.如图设O是正六边形ABCDEF的中心,写出图中
与向量OA相等的向量。
OA = DO = CB
变式一:与向量OA长度相等的向量
有多少个?
变式二:是否存在与向量OA长度相等,方向
相反的向量?
存在,为 FE
CB、DO、FE
变式三:与向量OA长度相等的共线向量有哪些?
例2.(1)如图, 四边形ABCD和ABDE都是平行四边形。
①与向量ED相等的向量有_______;
②若|AB|=3, 则|EC|=___________
A
E
D
C
B
(2)如图, 在2×4的方格纸中, 小方格的长度为1, 则图中与 a 相等的向量有_____个。
a
习题讲解
1.判断下列命题是否正确,若不正确,请简述理由. [来源:学科网ZXXK]
?
①向量 与 是共线向量,则A、B、C、D 四点必在一直线上;
②单位向量都相等;
③任一向量与它的相反向量(长度相同,方向相反的向量)不相等;
?
④共线的向量,若起点不同,则终点一定不同。
(×)
(×)
(×)
(×)
2.下面几个命题:
C
(3)若|a|=|b|,则a = b
(2)若|a|=0,则a = 0
|a|=|b|
a ∥ b
(4)两个向量a、b相等的充要条件是
(1)若a = b,b = c,则a = c。
当b ≠ 0时成立。
变:若 a ∥ b, b ∥ c, 则a ∥c
A.0 B. 1 C. 2 D. 3
其中正确的个数是( )
(5)若A、B、C、D是不共线的四点,则AB=DC是
四边形ABCD是平形四边形的充要条件。
A
B
D
C
B
A
C
D
习题讲解
巩
固
提
高
相同
相等
B
归纳小结
零向量、单位向量概念:
向量的概念:
向量的表示方法:
共线向量与平行向量关系:
平行向量定义:
相等向量定义:
课本 第77页习题2.1组 第2,3,5题
学海导航第37页
预习下一节
课后作业
