(新教材)2019--2020人教(重庆)物理必修第二册:第六章知识网络建构与学科素养提升同步导学案讲义含答案
文档属性
| 名称 | (新教材)2019--2020人教(重庆)物理必修第二册:第六章知识网络建构与学科素养提升同步导学案讲义含答案 | 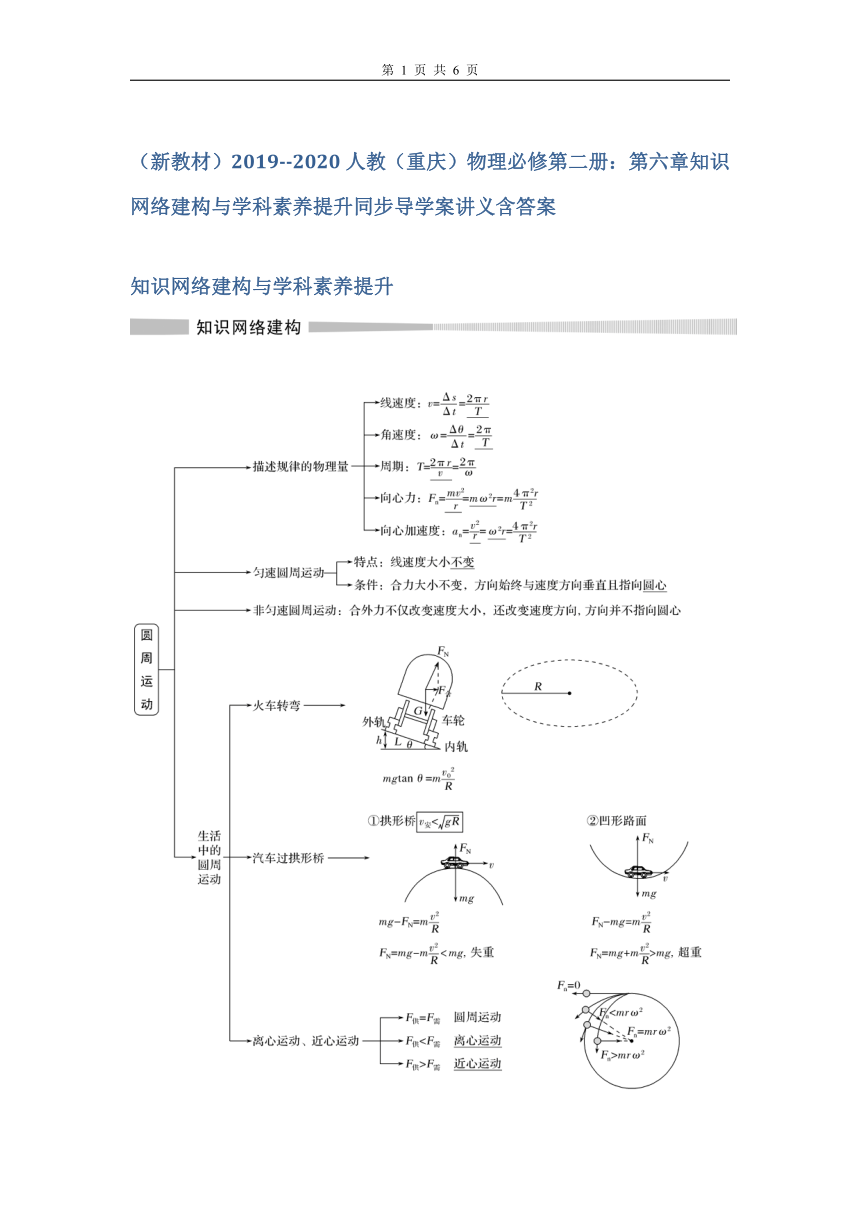 | |
| 格式 | zip | ||
| 文件大小 | 567.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-03-01 13:24:45 | ||
图片预览



文档简介
第 1 页 共 6 页
(新教材)2019--2020人教(重庆)物理必修第二册:第六章知识网络建构与学科素养提升同步导学案讲义含答案
知识网络建构与学科素养提升
一、圆周运动及其研究方法
1.描述圆周运动的几个物理量之间的关系
(1)v==rω,ω==,T===。
(2)Fn=m=mrω2=mvω=mr,an==rω2=vω=r。
注意:(1)上面各式有些仅适用于匀速圆周运动,有些适用于任何圆周运动。
(2)要注意各个物理量之间的瞬时对应关系。
2.分析圆周运动问题的关键及步骤
分析清楚向心力的来源是解决圆周运动问题的关键,分析向心力来源的步骤是:
(1)首先确定匀速圆周运动的圆周轨道所在的平面,其次找出轨道圆心的位置,然后分析做圆周运动物体所受的力,并作出受力示意图,最后找出这些力指向圆心方向的合外力就是向心力,如火车转弯、圆锥摆等问题。
(2)如果物体做变速圆周运动,它所受的合外力一般不是向心力,一般不指向圆心,但沿着半径方向的合力提供向心力,只有在某些特殊位置,合力才可能是向心力,如小球用绳拴着在竖直面内做圆周运动的最高点和最低点。
注意:当分析向心力来源时采用正交分解法,坐标原点就是做圆周运动的物体,一定有一个坐标轴的正方向沿着半径指向圆心。
[例1] 有一种杂技表演叫“飞车走壁”,由杂技演员驾驶摩托车沿光滑圆台形表演台的侧壁高速行驶,在水平面内做匀速圆周运动。图中粗线圆表示摩托车的行驶轨迹,轨迹离地面的高度为h。如果增大高度h,则下列关于摩托车的说法正确的是( )
A.对侧壁的压力FN增大
B.做圆周运动的周期T不变
C.做圆周运动的向心力Fn增大
D.做圆周运动的线速度增大
解析 摩托车做匀速圆周运动,提供圆周运动向心力的是重力mg和支持力FN′的合力,如图所示。
设表演台侧壁与竖直方向的夹角为α,侧壁对摩托车的支持力FN′=不变,即摩托车对侧壁的压力不变,选项A错误;向心力Fn=,m、α不变,向心力大小不变,选项C错误;根据牛顿第二定律得Fn=mr,h越高,r越大,Fn不变,则T越大,选项B错误;根据匀速圆周运动向心力公式得Fn=m,h越高,r越大,Fn不变,则v越大,选项D正确。
答案 D
[针对训练1] 如图,当汽车通过拱形桥顶点的速度为10 m/s时,车对桥顶的压力为车重的,如果要使汽车在桥面行驶至桥顶时,对桥面的压力为零,则汽车通过桥顶的速度应为( )
A.15 m/s B.20 m/s
C.25 m/s D.30 m/s
解析 当汽车通过拱形桥顶点的速度为10 m/s时,根据牛顿第二定律mg-FN=m,其中FN=;要使汽车在桥面行驶至桥顶时,对桥面的压力为零,则mg=m,联立解得v′=20 m/s,选项B正确。
答案 B
二、水平面内圆周运动的临界问题
1.不滑动
质量为m的物体在水平面上做圆周运动或随圆盘一起转动(如图所示)时,静摩擦力提供向心力,当静摩擦力达到最大值Ffm时,物体运动的速度也达到最大,即Ffm=meq \f(v,r),解得vm=。
2.与支持面或杆的弹力有关的临界问题
此问题要分析出恰好无支持力这一临界状态下的角速度(或线速度)等。
3.绳子被拉断
质量为m的物体被长为l的轻绳拴着(如图所示),且绕绳的另一端O在水平面内做匀速圆周运动,当绳子的拉力达到最大值Fm时,物体的速度最大,即
Fm=meq \f(v,l),解得vm=。
这就是物体在半径为l的圆周上运动的临界速度。
[例2] 如图所示,用一根长为l=1 m的细线,一端系一质量为m=1 kg的小球(可视为质点),另一端固定在一光滑锥体顶端,锥面与竖直方向的夹角θ=37°,当小球在水平面内绕锥体的轴做匀速圆周运动的角速度为ω时,细线的张力为FT。求:
(sin 37°=0.6,cos 37°=0.8,g取10 m/s2,结果可用根式表示)
(1)若要小球刚好离开锥面,则小球的角速度ω0至少为多大? 条件是什么?
(2)若细线与竖直方向的夹角为60°,则小球的角速度ω′为多大?
小球离开锥面了吗?
解析 (1)若要小球刚好离开锥面,则小球只受到重力和细线的拉力,受力分析如图所示。
小球做匀速圆周运动的轨迹圆在水平面上,故向心力水平,在水平方向运用牛顿第二定律及向心力公式得mgtan θ=mωlsin θ,解得ω=,即ω0== rad/s。
(2)当细线与竖直方向成60°角时,由牛顿第二定律及向心力公式得mgtan α=mω′2lsin α,解得ω′2=,即ω′==2 rad/s。
答案 (1) rad/s (2)2 rad/s
方法总结
(1)确定临界条件:判断题述的过程存在临界状态之后,要通过分析弄清临界状态出现的条件,并以数学形式表达出来。
(2)选择物理规律:当确定了物体运动的临界状态和临界条件后,对于不同的运动过程或现象,要分别选择相对应的物理规律,然后再列方程求解。
[针对训练2] 如图所示,水平转盘上放有一质量为m的物体(可视为质点),连接物体和转轴上的绳子长为r,物体与转盘间的最大静摩擦力是其压力的μ倍,g为重力加速度,转盘的角速度由零逐渐增大,求:
(1)绳子对物体的拉力为零时的最大角速度;
(2)当角速度为时,绳子对物体拉力的大小。
解析 (1)当恰由最大静摩擦力提供向心力时,绳子拉力为零,此时转速达到最大,如图甲所示,设此时转盘转动的角速度为ω0,则μmg=mωr,得ω0=。
(2)当ω=时,ω>ω0,所以绳子的拉力F和最大静摩擦力共同提供向心力,如图乙所示,此时,
F+μmg=mω2r,代入ω的值得F=μmg。
答案 (1) (2)μmg
(新教材)2019--2020人教(重庆)物理必修第二册:第六章知识网络建构与学科素养提升同步导学案讲义含答案
知识网络建构与学科素养提升
一、圆周运动及其研究方法
1.描述圆周运动的几个物理量之间的关系
(1)v==rω,ω==,T===。
(2)Fn=m=mrω2=mvω=mr,an==rω2=vω=r。
注意:(1)上面各式有些仅适用于匀速圆周运动,有些适用于任何圆周运动。
(2)要注意各个物理量之间的瞬时对应关系。
2.分析圆周运动问题的关键及步骤
分析清楚向心力的来源是解决圆周运动问题的关键,分析向心力来源的步骤是:
(1)首先确定匀速圆周运动的圆周轨道所在的平面,其次找出轨道圆心的位置,然后分析做圆周运动物体所受的力,并作出受力示意图,最后找出这些力指向圆心方向的合外力就是向心力,如火车转弯、圆锥摆等问题。
(2)如果物体做变速圆周运动,它所受的合外力一般不是向心力,一般不指向圆心,但沿着半径方向的合力提供向心力,只有在某些特殊位置,合力才可能是向心力,如小球用绳拴着在竖直面内做圆周运动的最高点和最低点。
注意:当分析向心力来源时采用正交分解法,坐标原点就是做圆周运动的物体,一定有一个坐标轴的正方向沿着半径指向圆心。
[例1] 有一种杂技表演叫“飞车走壁”,由杂技演员驾驶摩托车沿光滑圆台形表演台的侧壁高速行驶,在水平面内做匀速圆周运动。图中粗线圆表示摩托车的行驶轨迹,轨迹离地面的高度为h。如果增大高度h,则下列关于摩托车的说法正确的是( )
A.对侧壁的压力FN增大
B.做圆周运动的周期T不变
C.做圆周运动的向心力Fn增大
D.做圆周运动的线速度增大
解析 摩托车做匀速圆周运动,提供圆周运动向心力的是重力mg和支持力FN′的合力,如图所示。
设表演台侧壁与竖直方向的夹角为α,侧壁对摩托车的支持力FN′=不变,即摩托车对侧壁的压力不变,选项A错误;向心力Fn=,m、α不变,向心力大小不变,选项C错误;根据牛顿第二定律得Fn=mr,h越高,r越大,Fn不变,则T越大,选项B错误;根据匀速圆周运动向心力公式得Fn=m,h越高,r越大,Fn不变,则v越大,选项D正确。
答案 D
[针对训练1] 如图,当汽车通过拱形桥顶点的速度为10 m/s时,车对桥顶的压力为车重的,如果要使汽车在桥面行驶至桥顶时,对桥面的压力为零,则汽车通过桥顶的速度应为( )
A.15 m/s B.20 m/s
C.25 m/s D.30 m/s
解析 当汽车通过拱形桥顶点的速度为10 m/s时,根据牛顿第二定律mg-FN=m,其中FN=;要使汽车在桥面行驶至桥顶时,对桥面的压力为零,则mg=m,联立解得v′=20 m/s,选项B正确。
答案 B
二、水平面内圆周运动的临界问题
1.不滑动
质量为m的物体在水平面上做圆周运动或随圆盘一起转动(如图所示)时,静摩擦力提供向心力,当静摩擦力达到最大值Ffm时,物体运动的速度也达到最大,即Ffm=meq \f(v,r),解得vm=。
2.与支持面或杆的弹力有关的临界问题
此问题要分析出恰好无支持力这一临界状态下的角速度(或线速度)等。
3.绳子被拉断
质量为m的物体被长为l的轻绳拴着(如图所示),且绕绳的另一端O在水平面内做匀速圆周运动,当绳子的拉力达到最大值Fm时,物体的速度最大,即
Fm=meq \f(v,l),解得vm=。
这就是物体在半径为l的圆周上运动的临界速度。
[例2] 如图所示,用一根长为l=1 m的细线,一端系一质量为m=1 kg的小球(可视为质点),另一端固定在一光滑锥体顶端,锥面与竖直方向的夹角θ=37°,当小球在水平面内绕锥体的轴做匀速圆周运动的角速度为ω时,细线的张力为FT。求:
(sin 37°=0.6,cos 37°=0.8,g取10 m/s2,结果可用根式表示)
(1)若要小球刚好离开锥面,则小球的角速度ω0至少为多大? 条件是什么?
(2)若细线与竖直方向的夹角为60°,则小球的角速度ω′为多大?
小球离开锥面了吗?
解析 (1)若要小球刚好离开锥面,则小球只受到重力和细线的拉力,受力分析如图所示。
小球做匀速圆周运动的轨迹圆在水平面上,故向心力水平,在水平方向运用牛顿第二定律及向心力公式得mgtan θ=mωlsin θ,解得ω=,即ω0== rad/s。
(2)当细线与竖直方向成60°角时,由牛顿第二定律及向心力公式得mgtan α=mω′2lsin α,解得ω′2=,即ω′==2 rad/s。
答案 (1) rad/s (2)2 rad/s
方法总结
(1)确定临界条件:判断题述的过程存在临界状态之后,要通过分析弄清临界状态出现的条件,并以数学形式表达出来。
(2)选择物理规律:当确定了物体运动的临界状态和临界条件后,对于不同的运动过程或现象,要分别选择相对应的物理规律,然后再列方程求解。
[针对训练2] 如图所示,水平转盘上放有一质量为m的物体(可视为质点),连接物体和转轴上的绳子长为r,物体与转盘间的最大静摩擦力是其压力的μ倍,g为重力加速度,转盘的角速度由零逐渐增大,求:
(1)绳子对物体的拉力为零时的最大角速度;
(2)当角速度为时,绳子对物体拉力的大小。
解析 (1)当恰由最大静摩擦力提供向心力时,绳子拉力为零,此时转速达到最大,如图甲所示,设此时转盘转动的角速度为ω0,则μmg=mωr,得ω0=。
(2)当ω=时,ω>ω0,所以绳子的拉力F和最大静摩擦力共同提供向心力,如图乙所示,此时,
F+μmg=mω2r,代入ω的值得F=μmg。
答案 (1) (2)μmg
