人教A版高中数学 必修4-1.3 三角函数的诱导公式-课件(共21张PPT)
文档属性
| 名称 | 人教A版高中数学 必修4-1.3 三角函数的诱导公式-课件(共21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 673.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-03 08:40:09 | ||
图片预览








文档简介
(共21张PPT)
三角函数的诱导公式
------(五、六)
人教版高中必修四
函数名不变,符号看象限
一、复习
1.求下列各三角函数的值
2.化简
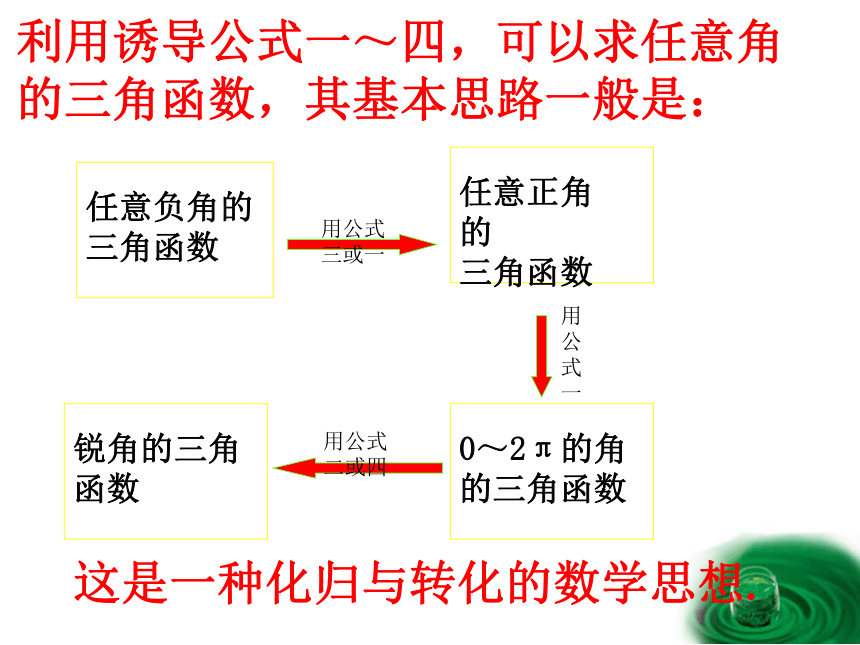
利用诱导公式一~四,可以求任意角的三角函数,其基本思路一般是:
这是一种化归与转化的数学思想.
用公式三或一
用公式一
用公式二或四
1.诱导公式一、二、三、四分别反映了2kπ+α(k∈Z)、π+α、-α、 π-α与α的三角函数之间的关系,这四组公式的共同特点是:
函数名不变,符号看象限.
学习目标:
1.了解角 与 的正弦、余弦公式的推导过程
2.熟记并应用角 的诱导公式进行求值、化简
1.sin(90°-60°)与sin60°
的值相等吗?相反吗?
2.sin(90°-60°)与cos60°,
cos(90°-60°)与sin60°的值分别
有什么关系?据此,你有什么猜想?
合作研讨:
1.如果α为锐角,你有什么办法证明,
思考5:点P1(x,y)关于直线y=x对称的点P2的坐标如何?
α的终边
公式五:
公式六:
思考:正弦函数与余弦函数互称为异名函数,你能概括一下公式五、六的共同特点和规律吗?
1.将下列三角函数化为0度到45度之间的三角函数
2.求下列各式的值
3 化简:
思考5:根据相关诱导公式推导,
2.诱导公式是三角变换的基本公式,其中角α是任意角,应用时要注意整体把握、灵活变通.
小结作业
1.诱导公式反映了各种不同形式的角的三角函数之间的相互关系,并具有一定的规律性,“奇变偶不变,符号看象限”,是记住这些公式的有效方法.
作业:
1.册子14下-15上
2.本子课本28页第7题
29页A组第3题,B组1-2
三角函数的诱导公式
------(五、六)
人教版高中必修四
函数名不变,符号看象限
一、复习
1.求下列各三角函数的值
2.化简
利用诱导公式一~四,可以求任意角的三角函数,其基本思路一般是:
这是一种化归与转化的数学思想.
用公式三或一
用公式一
用公式二或四
1.诱导公式一、二、三、四分别反映了2kπ+α(k∈Z)、π+α、-α、 π-α与α的三角函数之间的关系,这四组公式的共同特点是:
函数名不变,符号看象限.
学习目标:
1.了解角 与 的正弦、余弦公式的推导过程
2.熟记并应用角 的诱导公式进行求值、化简
1.sin(90°-60°)与sin60°
的值相等吗?相反吗?
2.sin(90°-60°)与cos60°,
cos(90°-60°)与sin60°的值分别
有什么关系?据此,你有什么猜想?
合作研讨:
1.如果α为锐角,你有什么办法证明,
思考5:点P1(x,y)关于直线y=x对称的点P2的坐标如何?
α的终边
公式五:
公式六:
思考:正弦函数与余弦函数互称为异名函数,你能概括一下公式五、六的共同特点和规律吗?
1.将下列三角函数化为0度到45度之间的三角函数
2.求下列各式的值
3 化简:
思考5:根据相关诱导公式推导,
2.诱导公式是三角变换的基本公式,其中角α是任意角,应用时要注意整体把握、灵活变通.
小结作业
1.诱导公式反映了各种不同形式的角的三角函数之间的相互关系,并具有一定的规律性,“奇变偶不变,符号看象限”,是记住这些公式的有效方法.
作业:
1.册子14下-15上
2.本子课本28页第7题
29页A组第3题,B组1-2
