人教A版高中数学必修4-1.3 三角函数的诱导公式-课件(共24张PPT)
文档属性
| 名称 | 人教A版高中数学必修4-1.3 三角函数的诱导公式-课件(共24张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 743.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-03 08:42:37 | ||
图片预览







文档简介
(共24张PPT)
三角函数的诱导公式1
热身训练
已知在△ABC中,
回顾练习:求下列三角函数值.
(1)sin 405? ; (2)cos 390 ? ;
(3)cos (-300 ?) ;
知识新授:
公式一
公式二:
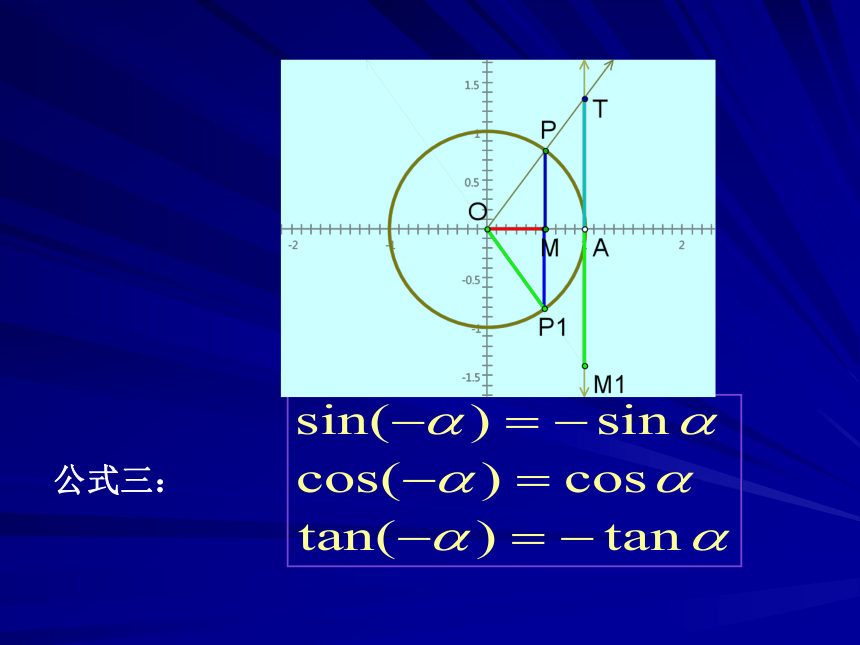
公式三:
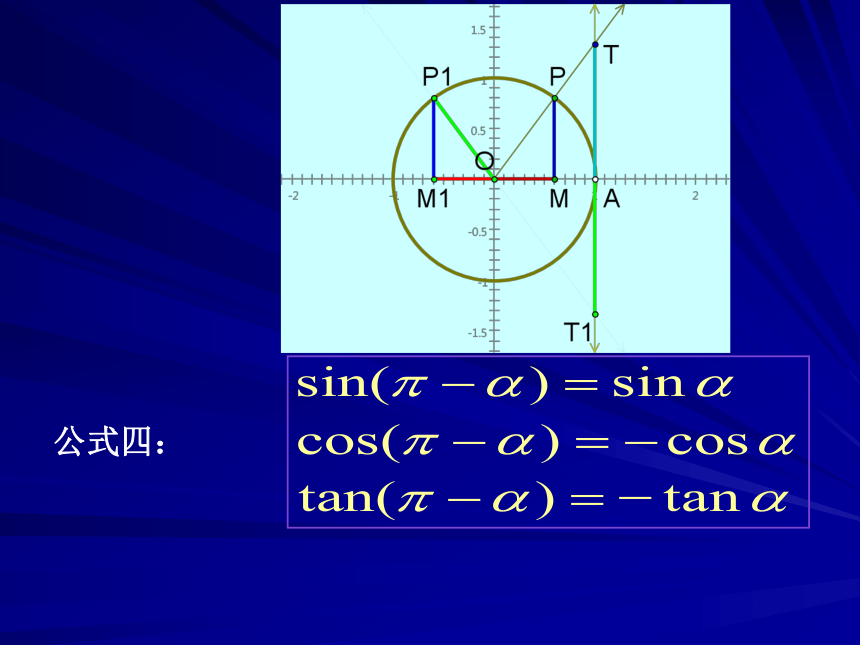
公式四:
公式二:
公式三:
公式四:
公式一:
函数名不变
符号看象限
利用诱导公式可以把任意角的三角函数值转化为锐角的三角函数值,基本步骤是:负化正,大化小,化为锐角再定值。
例四:(给值求值)
1)已知
探究两角(或整体角)之间的关系(一般相加或相减),利用已知角的三角函数值和诱导公式,来求未知角的三角函数值!体现了化归思想!
公式二:
公式三:
公式四:
公式一:
函数名不变
符号看象限
课堂小结:
公式的实质是将终边对称的图形关系“翻译”成代数关系;
公式的作用是将复杂角的三角函数化为简单三角函数.
三角函数的诱导公式2
函数名不变
符号看象限
知识回顾:
公式五:
知识新授:
公式六:
公式五:
公式六:
公式五:
公式六:
纵变横不变
符号看象限
例1.证明:
例2.化简:
例题讲解:
例3. 已知cos(75 +α)= ,且-180 <α<-90 ,
求cos(15 -α)的值.
0
0
0
0
1
3
例四:(给值求值)
1)已知
探究两角(或整体角)之间的关系(一般相加或相减),利用已知角的三角函数值和诱导公式,来求未知角的三角函数值!体现了化归思想!
课堂练习:
在△ABC中,求证:cos(A+B)=-cosC,
sin(3A+3B)=sin3C.
一定要注意三角形中内角的关系:三个内角之和为180°,A+B=180°—C
三角函数的诱导公式1
热身训练
已知在△ABC中,
回顾练习:求下列三角函数值.
(1)sin 405? ; (2)cos 390 ? ;
(3)cos (-300 ?) ;
知识新授:
公式一
公式二:
公式三:
公式四:
公式二:
公式三:
公式四:
公式一:
函数名不变
符号看象限
利用诱导公式可以把任意角的三角函数值转化为锐角的三角函数值,基本步骤是:负化正,大化小,化为锐角再定值。
例四:(给值求值)
1)已知
探究两角(或整体角)之间的关系(一般相加或相减),利用已知角的三角函数值和诱导公式,来求未知角的三角函数值!体现了化归思想!
公式二:
公式三:
公式四:
公式一:
函数名不变
符号看象限
课堂小结:
公式的实质是将终边对称的图形关系“翻译”成代数关系;
公式的作用是将复杂角的三角函数化为简单三角函数.
三角函数的诱导公式2
函数名不变
符号看象限
知识回顾:
公式五:
知识新授:
公式六:
公式五:
公式六:
公式五:
公式六:
纵变横不变
符号看象限
例1.证明:
例2.化简:
例题讲解:
例3. 已知cos(75 +α)= ,且-180 <α<-90 ,
求cos(15 -α)的值.
0
0
0
0
1
3
例四:(给值求值)
1)已知
探究两角(或整体角)之间的关系(一般相加或相减),利用已知角的三角函数值和诱导公式,来求未知角的三角函数值!体现了化归思想!
课堂练习:
在△ABC中,求证:cos(A+B)=-cosC,
sin(3A+3B)=sin3C.
一定要注意三角形中内角的关系:三个内角之和为180°,A+B=180°—C
