2019-2020学年数学新人教A版必修4学案:1.1.2弧度制Word版含答案
文档属性
| 名称 | 2019-2020学年数学新人教A版必修4学案:1.1.2弧度制Word版含答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 62.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-03 00:00:00 | ||
图片预览

文档简介
1.1.2弧度制
一、三维目标:
知识与技能:(1)理解弧度制的定义,能正确地进行角度与弧度的换算,熟记特殊角的弧度数;
(2)能够推导弧度制下的弧长公式,扇形的面积公式并熟记;(3)能熟练的用弧度制表示角的集合。
过程与方法:通过学习,认识到角度制、弧度制都是度量角的制度,二者虽然单位不同,但是互相联系的、辩证统一的,进一步加强对辩证统一思想的理解。
情感态度与价值观:通过总结引入弧度制的好处,学会归纳、整理并认识到任何新知识的产生都有它存在的必要性,都会为我们解决现实问题带来方便,从而激发学生的求知欲。
二、学习重点难点:
重点:1.弧度制的定义.2.用弧度制表示的弧长公式、扇形面积公式。
3.角度制与弧度制的换算4.角的集合与实数集R之间建立的一一对应关系。
难点:对弧度制定义的理解;建立弧度制的意义。
三、学法指导:认真阅读教材的6-9页内容,理解弧度制的定义是基础,掌握角度与弧度的换算关系是关键。理解弧度作为角的度量单位的可靠性和可行性,运算时要熟练使用弧度制。
四、知识链接:
1.角可以看成平面内一条 绕着 从一个位置旋转到另一个位置所成的图形。
2.按逆时针方向旋转形成的角叫做 ,按顺时针方向旋转形成的角叫做 .如果一条射线没有作任何旋转,我们称它形成了一个 。
它的 与 重合.这样,我们就把角的概念推广到了 ,
包括 、 和 。
3.我们常在 内讨论角.为了讨论问题的方便,我们使角的 与 重合,角的 与 重合.那么,角的 终边在第几象限,我们就说这个角是 。
如果角的终边在坐标轴上,就认为这个角 。 4.所有与角终边相同的角,连同角在内,可构成一个 ,即 。
5.角度制:我们把用度做单位来度量角的制度叫做角度制。周角的1/360为1度的角。这种用度作为单位来度量角的单位制叫做角度制。
五、学习过程:
弧度制
A问题1:弧度制的定义是什么?写法和读法、图形表示分别是什么?
注:今后在用弧度制表示角的时候,弧度二字或rad可以略去不写。
A练习:下列各命题中,真命题是( )
A.一弧度就是一度的圆心角所对的弧
B.一弧度是长度为半径的弧
C.一弧度是长度等于半径的弧所对的圆心角,它是角的一种度量单位
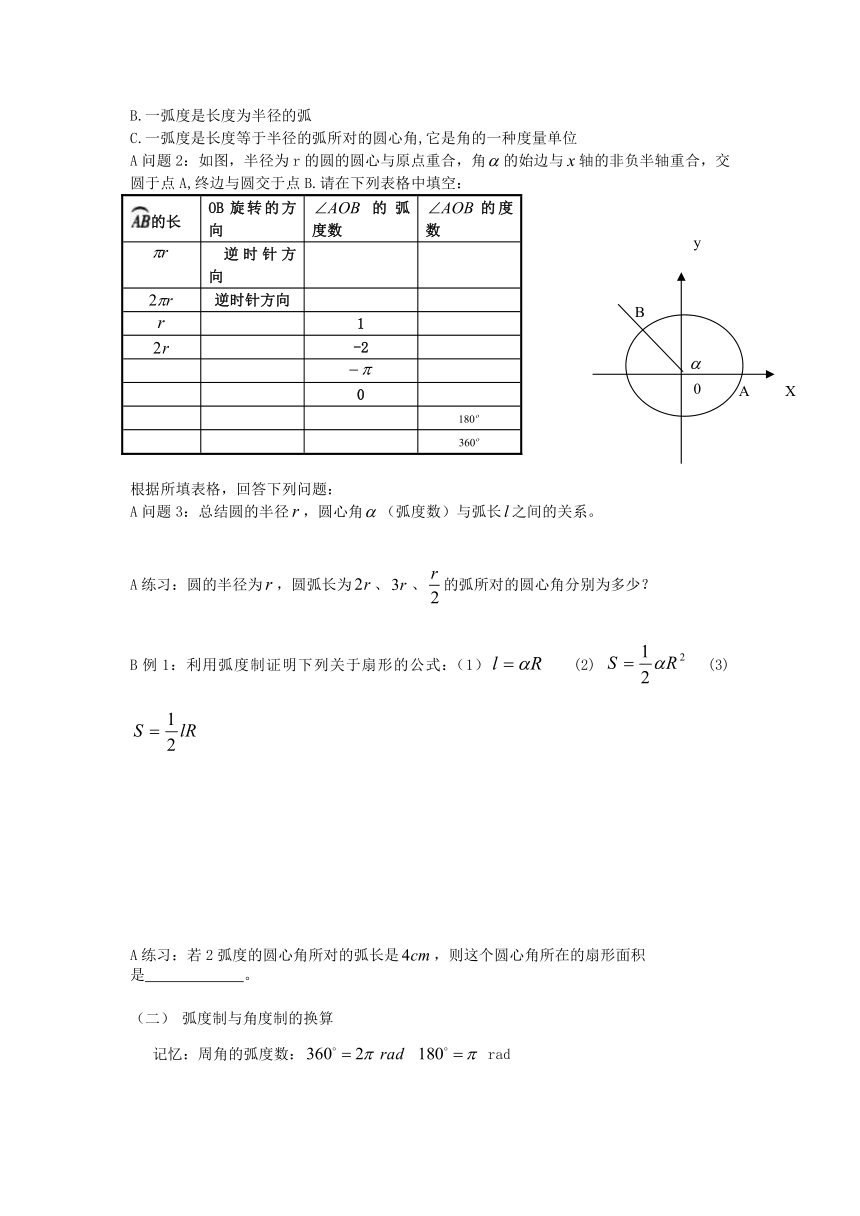
A问题2:如图,半径为r的圆的圆心与原点重合,角的始边与轴的非负半轴重合,交圆于点A,终边与圆交于点B.请在下列表格中填空:
的长
OB旋转的方向
的弧度数
的度数
逆时针方向
逆时针方向
1
-2
0
根据所填表格,回答下列问题:
A问题3:总结圆的半径,圆心角(弧度数)与弧长之间的关系。
A练习:圆的半径为,圆弧长为、、的弧所对的圆心角分别为多少?
B例1:利用弧度制证明下列关于扇形的公式:(1) (2) (3)
A练习:若2弧度的圆心角所对的弧长是,则这个圆心角所在的扇形面积是 。
弧度制与角度制的换算
记忆:周角的弧度数: rad
换算公式:rad 1=
rad= rad.
B问题4:运用换算公式填表(并记住):
度
弧度
B例2:用弧度制分别表示轴线角、象限角的集合。
(1)第一、二、三、四象限角的弧度表示。
(2)终边在轴上的角的集合、终边在轴上的角的集合、终边在坐标轴上的角的集合。
C例3:(1)已知是第一象限角,那么是( )
A、第一象限角 B、第二象限角
C 第一或第二象限角或终边落在上的角 D、第一或第二象限角
(2) 已知是第一象限角,那么是( )
A、第一象限角 B、第二象限角
C、、小于的正角 D、第一或第三象限角
六、达标检测:
B1.下列各命题中,真命题是 (填序号)。
①“度”与“弧度”是度量角的两种不同的度量单位;
② 1弧度是长度等于半径长的弧所对的圆心角;
③根据弧度的定义,180°一定等于π弧度;
④不论用角度制还是弧度制度量角,它们均与圆的半径长短有关.
⑤一条弦的长等于半径,这条弦所对的圆心角大于一弧度的角
A2.填空:(1)-300°= rad;(2) π= 度。
B3.若是第四象限的角,则在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
B4.解答下列各题:
(1)已知扇形的周长为10cm,面积为4cm2,求扇形圆心角的弧度数;
(2)已知一扇形的周长为40cm,当它的半径和圆心角取什么值时,才能使扇形的面积最大?最大面积是多少?
B5.已知集合 ,
则 等于 ( )
A. B.{}
C. D.或}
B6.把表示成的形式,则为( )
A. B. C. D.
B7.写出阴影部分的角的集合:
七、学习小结:
1.弧度制的定义。
2.角度制与弧度制的换算。
八、课后反思:
1.1.2弧度制的答案
例2(1)(2)
例3(1)C (2) D
【达标检测】
1①②③⑤ 2 ; 3 C
4【解析】(1)设扇形圆心角的弧度数为θ(0<θ<2π), 弧长为l,半径为r,
依题意有 l+2r=10 ①
lr=4 ②
①代入②得r2-5r+4=0,解之得r1=1,r2=4.
当r=1时,l=8(cm),此时,θ=8rad>2πrad(舍去).
当r=4时,l=2(cm),此时,θ= = 0.5 rad.
(2)设扇形的圆心角为θ,半径为r,弧长为l,面积为S,则l+2r=40,∴l=40-2r,
∴S= lr= ×(40-2r)r=20r-r2=-r(r-10)2+100.
∴当半径r=10cm时,扇形的面积最大,这个最大值为100cm2,这时θ===2(弧度)
5 D 6C
7;
一、三维目标:
知识与技能:(1)理解弧度制的定义,能正确地进行角度与弧度的换算,熟记特殊角的弧度数;
(2)能够推导弧度制下的弧长公式,扇形的面积公式并熟记;(3)能熟练的用弧度制表示角的集合。
过程与方法:通过学习,认识到角度制、弧度制都是度量角的制度,二者虽然单位不同,但是互相联系的、辩证统一的,进一步加强对辩证统一思想的理解。
情感态度与价值观:通过总结引入弧度制的好处,学会归纳、整理并认识到任何新知识的产生都有它存在的必要性,都会为我们解决现实问题带来方便,从而激发学生的求知欲。
二、学习重点难点:
重点:1.弧度制的定义.2.用弧度制表示的弧长公式、扇形面积公式。
3.角度制与弧度制的换算4.角的集合与实数集R之间建立的一一对应关系。
难点:对弧度制定义的理解;建立弧度制的意义。
三、学法指导:认真阅读教材的6-9页内容,理解弧度制的定义是基础,掌握角度与弧度的换算关系是关键。理解弧度作为角的度量单位的可靠性和可行性,运算时要熟练使用弧度制。
四、知识链接:
1.角可以看成平面内一条 绕着 从一个位置旋转到另一个位置所成的图形。
2.按逆时针方向旋转形成的角叫做 ,按顺时针方向旋转形成的角叫做 .如果一条射线没有作任何旋转,我们称它形成了一个 。
它的 与 重合.这样,我们就把角的概念推广到了 ,
包括 、 和 。
3.我们常在 内讨论角.为了讨论问题的方便,我们使角的 与 重合,角的 与 重合.那么,角的 终边在第几象限,我们就说这个角是 。
如果角的终边在坐标轴上,就认为这个角 。 4.所有与角终边相同的角,连同角在内,可构成一个 ,即 。
5.角度制:我们把用度做单位来度量角的制度叫做角度制。周角的1/360为1度的角。这种用度作为单位来度量角的单位制叫做角度制。
五、学习过程:
弧度制
A问题1:弧度制的定义是什么?写法和读法、图形表示分别是什么?
注:今后在用弧度制表示角的时候,弧度二字或rad可以略去不写。
A练习:下列各命题中,真命题是( )
A.一弧度就是一度的圆心角所对的弧
B.一弧度是长度为半径的弧
C.一弧度是长度等于半径的弧所对的圆心角,它是角的一种度量单位
A问题2:如图,半径为r的圆的圆心与原点重合,角的始边与轴的非负半轴重合,交圆于点A,终边与圆交于点B.请在下列表格中填空:
的长
OB旋转的方向
的弧度数
的度数
逆时针方向
逆时针方向
1
-2
0
根据所填表格,回答下列问题:
A问题3:总结圆的半径,圆心角(弧度数)与弧长之间的关系。
A练习:圆的半径为,圆弧长为、、的弧所对的圆心角分别为多少?
B例1:利用弧度制证明下列关于扇形的公式:(1) (2) (3)
A练习:若2弧度的圆心角所对的弧长是,则这个圆心角所在的扇形面积是 。
弧度制与角度制的换算
记忆:周角的弧度数: rad
换算公式:rad 1=
rad= rad.
B问题4:运用换算公式填表(并记住):
度
弧度
B例2:用弧度制分别表示轴线角、象限角的集合。
(1)第一、二、三、四象限角的弧度表示。
(2)终边在轴上的角的集合、终边在轴上的角的集合、终边在坐标轴上的角的集合。
C例3:(1)已知是第一象限角,那么是( )
A、第一象限角 B、第二象限角
C 第一或第二象限角或终边落在上的角 D、第一或第二象限角
(2) 已知是第一象限角,那么是( )
A、第一象限角 B、第二象限角
C、、小于的正角 D、第一或第三象限角
六、达标检测:
B1.下列各命题中,真命题是 (填序号)。
①“度”与“弧度”是度量角的两种不同的度量单位;
② 1弧度是长度等于半径长的弧所对的圆心角;
③根据弧度的定义,180°一定等于π弧度;
④不论用角度制还是弧度制度量角,它们均与圆的半径长短有关.
⑤一条弦的长等于半径,这条弦所对的圆心角大于一弧度的角
A2.填空:(1)-300°= rad;(2) π= 度。
B3.若是第四象限的角,则在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
B4.解答下列各题:
(1)已知扇形的周长为10cm,面积为4cm2,求扇形圆心角的弧度数;
(2)已知一扇形的周长为40cm,当它的半径和圆心角取什么值时,才能使扇形的面积最大?最大面积是多少?
B5.已知集合 ,
则 等于 ( )
A. B.{}
C. D.或}
B6.把表示成的形式,则为( )
A. B. C. D.
B7.写出阴影部分的角的集合:
七、学习小结:
1.弧度制的定义。
2.角度制与弧度制的换算。
八、课后反思:
1.1.2弧度制的答案
例2(1)(2)
例3(1)C (2) D
【达标检测】
1①②③⑤ 2 ; 3 C
4【解析】(1)设扇形圆心角的弧度数为θ(0<θ<2π), 弧长为l,半径为r,
依题意有 l+2r=10 ①
lr=4 ②
①代入②得r2-5r+4=0,解之得r1=1,r2=4.
当r=1时,l=8(cm),此时,θ=8rad>2πrad(舍去).
当r=4时,l=2(cm),此时,θ= = 0.5 rad.
(2)设扇形的圆心角为θ,半径为r,弧长为l,面积为S,则l+2r=40,∴l=40-2r,
∴S= lr= ×(40-2r)r=20r-r2=-r(r-10)2+100.
∴当半径r=10cm时,扇形的面积最大,这个最大值为100cm2,这时θ===2(弧度)
5 D 6C
7;
