北师大版高中数学必修四《余弦函数图形与性质》课件(共19张PPT)
文档属性
| 名称 | 北师大版高中数学必修四《余弦函数图形与性质》课件(共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 556.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-03 08:39:03 | ||
图片预览




文档简介
(共19张PPT)
余弦函数的图像与性质
1、诱导公式(k ? Z)
sin(x+2k ? )=
cos(x+2k ? )=
cos( - x ) =
sin( x + )=
2、如何作正弦函数y =sinx ,x∈R的图象?(正弦曲线)
sinx
cosx
cosx
cosx
温故知新
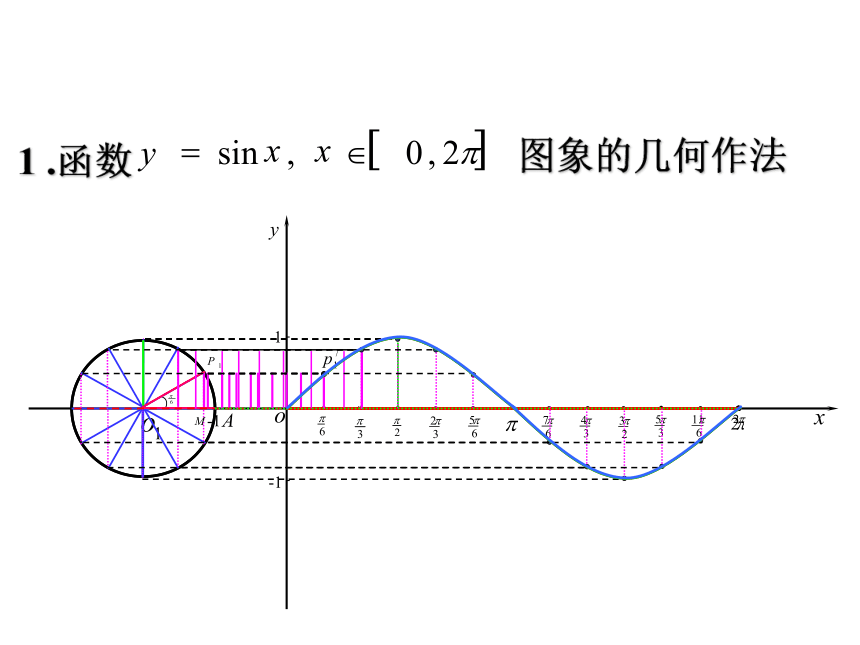
1 .函数
图象的几何作法
-
-
-1
1
-
-
-1
-
-
[
]
p
2
,
0
,
sin
?
=
x
x
y
y
x
o
1
-1
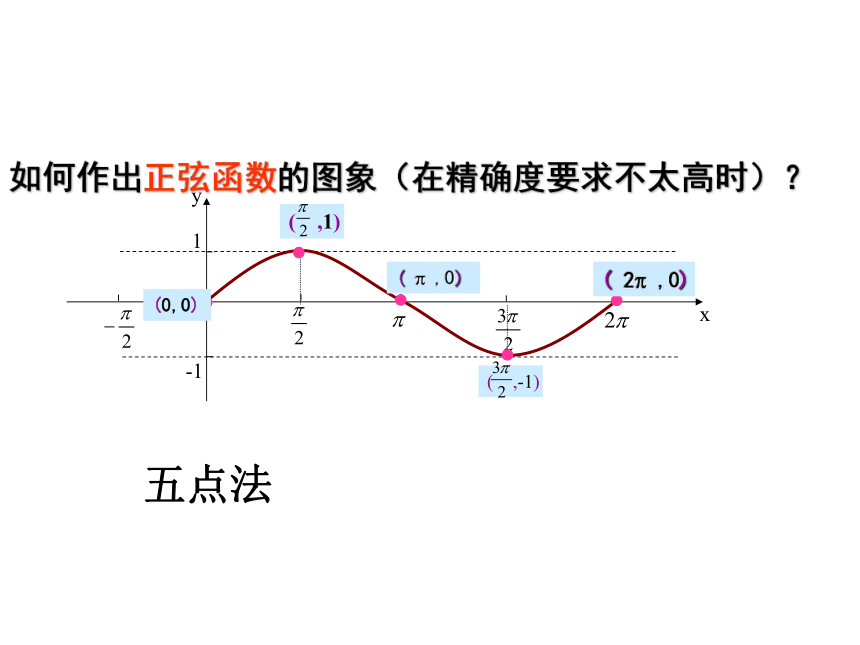
如何作出正弦函数的图象(在精确度要求不太高时)?
(0,0)
( ,1)
( ? ,0)
( ,-1)
( 2? ,0)
五点法
x
6?
y
o
-?
-1
2?
3?
4?
5?
-2?
-3?
-4?
1
?
y
x
o
1
-1
y=sinx , x?[0,2?]
正弦曲线
y=sinx,x?R
sin(x+2k?)=sinx, k?Z
f(x+2k?)=f(x),利用图像平移
由y= sin x y=sin(x+ )
图像作何变化?
向左平移 个单位长度
二、合作探究
1、余弦函数的图像(图像平移)
x
6?
y
o
-?
-1
2?
3?
4?
5?
-2?
-3?
-4?
1
?
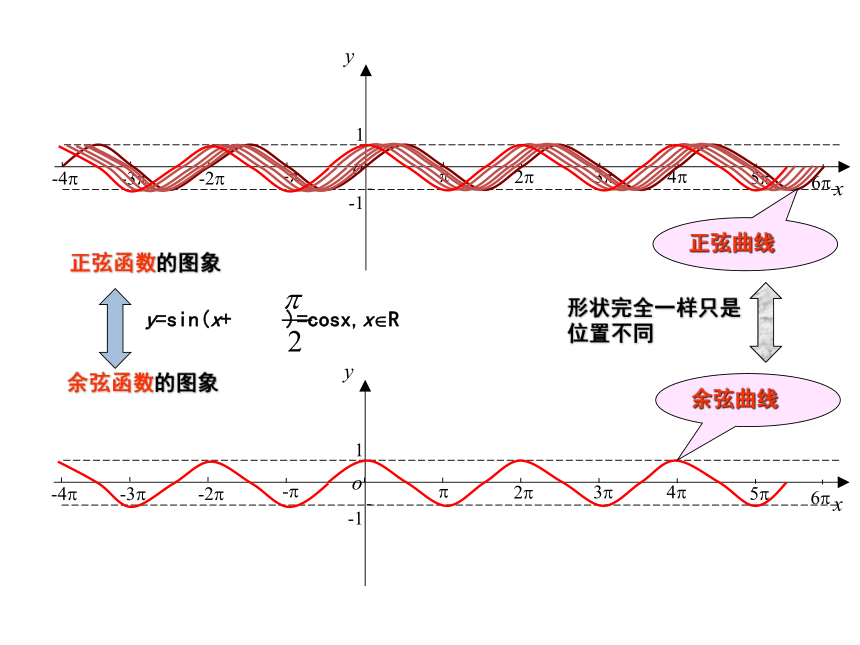
余弦函数的图象
正弦函数的图象
x
6?
y
o
-?
-1
2?
3?
4?
5?
-2?
-3?
-4?
1
?
y=sin(x+ )=cosx,x?R
余弦曲线
正弦曲线
形状完全一样只是位置不同
-
-
-
-1
1
-
-1
在函数 的图象上,起关键作用的点有:
最高点:
最低点:
与x轴的交点:
(0,1)
2、余弦函数的图像(五点法作图)
关键五点 (y=sinx,x?[0,2?])
-
-
-1
1
-
-1
-
-
-
-1
1
-
-1
关键五点 (y=cosx,x?[0,2?] )
观察图像正余弦函数图像上五个关键点,完成下表
三角
函数 最高点 最低点 与X轴的交点
y=sinx
y=cosx
余弦曲线:y=cosx,x∈R
定义域:R 值域:【-1,1】
单调性:
奇偶性:偶函数
周期性:
对称轴:y 轴
对称中心:
3、余弦函数的性质
定义域
周 期
奇偶性
函数
性质
R
R
y=sinx
y=cosx
奇函数:图像关于原点对称
偶函数:图像关于y轴对称
单调性
值 域
提升总结:正弦和余弦函数的性质对比
x
sinx
0 ? 2 ?
0
1
0
-1
0
1、在同一坐标系内,用五点法分别画出函数
x?[0, 2?] 和 y= cosx,x?[ , ]的简图:
o
1
y
x
-1
2
y=sinx,x?[0, 2?]
y= cosx,x?[ , ]
向左平移 个单位长度
x
cosx
1
0
0
-1
0
0 ?
o
1
y
x
-1
2
三、应用提升
y= sinx,
-
-
-1
1
-
-1
-
-
2、在 [0, 2?] 上,使 cosx=sinx 成立的X的取值
是多少?
cosx﹤sinx
cosx > sinx 呢?
呢?
2、试画出下列函数在区间[0, 2?] 上的简图,并说说其性质:
1)y=2cosx
2)y=cosx-2
3)y=-cosx
5)y=cos︱x ︳
4)y=︱cosx︱
3.不求值比较下列两个三角函数值的大小.
Cosx=
4、当X∈ [0, 2?]时,
求 不 等 式cosx>
的 解 集?
-
-
-
-1
1
-
-1
Cosx<
5、函 数 f(x)= cosx + 2 ︱cosx︱,
x∈[0, 2?] 的图 像 与 直 线 y=k
有 且 仅有 两 个 不 同 的 交 点,
则 k 的 取 值 范 围 是______
(1, 3]
课堂小结:
1、五点法做余弦函数的图像
2、余弦函数的性质。
余弦函数的图像与性质
1、诱导公式(k ? Z)
sin(x+2k ? )=
cos(x+2k ? )=
cos( - x ) =
sin( x + )=
2、如何作正弦函数y =sinx ,x∈R的图象?(正弦曲线)
sinx
cosx
cosx
cosx
温故知新
1 .函数
图象的几何作法
-
-
-1
1
-
-
-1
-
-
[
]
p
2
,
0
,
sin
?
=
x
x
y
y
x
o
1
-1
如何作出正弦函数的图象(在精确度要求不太高时)?
(0,0)
( ,1)
( ? ,0)
( ,-1)
( 2? ,0)
五点法
x
6?
y
o
-?
-1
2?
3?
4?
5?
-2?
-3?
-4?
1
?
y
x
o
1
-1
y=sinx , x?[0,2?]
正弦曲线
y=sinx,x?R
sin(x+2k?)=sinx, k?Z
f(x+2k?)=f(x),利用图像平移
由y= sin x y=sin(x+ )
图像作何变化?
向左平移 个单位长度
二、合作探究
1、余弦函数的图像(图像平移)
x
6?
y
o
-?
-1
2?
3?
4?
5?
-2?
-3?
-4?
1
?
余弦函数的图象
正弦函数的图象
x
6?
y
o
-?
-1
2?
3?
4?
5?
-2?
-3?
-4?
1
?
y=sin(x+ )=cosx,x?R
余弦曲线
正弦曲线
形状完全一样只是位置不同
-
-
-
-1
1
-
-1
在函数 的图象上,起关键作用的点有:
最高点:
最低点:
与x轴的交点:
(0,1)
2、余弦函数的图像(五点法作图)
关键五点 (y=sinx,x?[0,2?])
-
-
-1
1
-
-1
-
-
-
-1
1
-
-1
关键五点 (y=cosx,x?[0,2?] )
观察图像正余弦函数图像上五个关键点,完成下表
三角
函数 最高点 最低点 与X轴的交点
y=sinx
y=cosx
余弦曲线:y=cosx,x∈R
定义域:R 值域:【-1,1】
单调性:
奇偶性:偶函数
周期性:
对称轴:y 轴
对称中心:
3、余弦函数的性质
定义域
周 期
奇偶性
函数
性质
R
R
y=sinx
y=cosx
奇函数:图像关于原点对称
偶函数:图像关于y轴对称
单调性
值 域
提升总结:正弦和余弦函数的性质对比
x
sinx
0 ? 2 ?
0
1
0
-1
0
1、在同一坐标系内,用五点法分别画出函数
x?[0, 2?] 和 y= cosx,x?[ , ]的简图:
o
1
y
x
-1
2
y=sinx,x?[0, 2?]
y= cosx,x?[ , ]
向左平移 个单位长度
x
cosx
1
0
0
-1
0
0 ?
o
1
y
x
-1
2
三、应用提升
y= sinx,
-
-
-1
1
-
-1
-
-
2、在 [0, 2?] 上,使 cosx=sinx 成立的X的取值
是多少?
cosx﹤sinx
cosx > sinx 呢?
呢?
2、试画出下列函数在区间[0, 2?] 上的简图,并说说其性质:
1)y=2cosx
2)y=cosx-2
3)y=-cosx
5)y=cos︱x ︳
4)y=︱cosx︱
3.不求值比较下列两个三角函数值的大小.
Cosx=
4、当X∈ [0, 2?]时,
求 不 等 式cosx>
的 解 集?
-
-
-
-1
1
-
-1
Cosx<
5、函 数 f(x)= cosx + 2 ︱cosx︱,
x∈[0, 2?] 的图 像 与 直 线 y=k
有 且 仅有 两 个 不 同 的 交 点,
则 k 的 取 值 范 围 是______
(1, 3]
课堂小结:
1、五点法做余弦函数的图像
2、余弦函数的性质。
