人教版高中物理必修2 7.2 功-课件(共15张PPT)
文档属性
| 名称 | 人教版高中物理必修2 7.2 功-课件(共15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-03-01 00:00:00 | ||
图片预览





文档简介
(共15张PPT)
第七章 机械能守恒定律
第二节
一、新课引入
如图所示,木材被起重机举高,重力势能增加了;列车在机车的牵引下加速前进,动能增加了;用力压缩握力器后,握力器的弹性势能增加了。
现象:
思考:这些现象都有一个共同的特征,你能看出来吗?
木材在起重机的拉力作用下重力势能增加了
列车在机车牵引力作用下 动能增加了
握力器在手的压力作用下弹性势能增加了
物体的能量都发生了变化,
结论:
为了定量表达能量的变化,科学家引入功这个概念。
三、新课讲解
(一) 功的概念
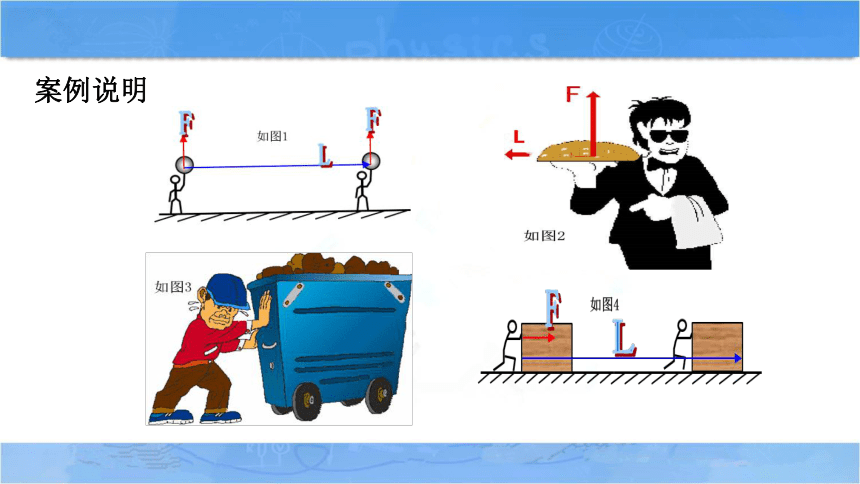
如果一个物体受到力的作用, 并且在力的方向上发生了位移, 我们就说这个力对物体做了功.
案例说明
归纳:做功的两个必要条件
(1)作用在物体上的力.
(2)物体在力的方向发生一段位移
这两个条件是严格的,缺一不可 !
(二)功的表达式
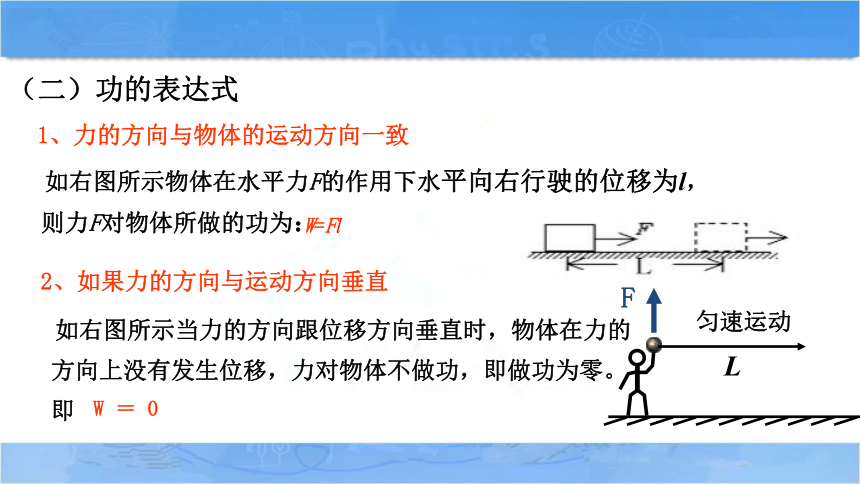
1、力的方向与物体的运动方向一致
如右图所示物体在水平力F的作用下水平向右行驶的位移为l,则力F对物体所做的功为:
2、如果力的方向与运动方向垂直
如右图所示当力的方向跟位移方向垂直时,物体在力的方向上没有发生位移,力对物体不做功,即做功为零。 即
F
匀速运动
L
W=Fl
W = 0
3、当力的方向与位移方向成某一角度时
如右图所示物体m在与水平方向成α角的力F的作用下,沿水平方向向右行驶的距离为l,求力F对物体所做的功。
思路:
转化思想+
力或位移的 矢量性合矢量与两个分矢量等效
方法①
将位移l沿力方向和垂直于力方向分解如图所示,则沿力方向的位移l1=lcosα,垂直于力方向的位移l2=lsinα.
得出
方法②
将力F沿位移方向和垂直于位移方向分解如图所示,则沿位移方向的力F1=Fcosα,垂直于位移方向的力F2=Fsinα.
得出
W=Fl1=Flcosα.
W=F 1l =Fcosα l=Flcosα .
结论:力对物体做的功,等于这个力的大小、位移的大小、力和位移方
向夹角的余弦值的乘积,W=Flcosα.
①F是作用在物体上的力,必需是恒力,变力做功不能直接套用公式计算。
②l是物体发生的位移。
③α是F的方向和l的方向的夹角, 0~180°
④功是标量,只有大小没有方向。
特别提醒:
(三)功的正负
W=Flcosa
F
L
1、当α=0时,W =Fl
力F对物体做正功。
F
L
2、当α=π/2时,W =0
力F对物体没做功
F
L
3、当α<π/2时,W>0
力F对物体做正功。
F
L
4、当π/2 <α≤ π时,W <0
力F对物体做负功。
也叫做物体克服力F做功
意义 动力学角度 能 量 角 度
正功 力对物体做正功,这个力对物体来说是动力. 力对物体(或系统)做正功,外界向物体(或系统)提供能量,即正功表示受力物体(或系统)获得能量.
负功 力对物体做负功,这个力对物体来说是阻力. 力对物体(或系统)做负功,向外界输出能量,即负功表示物体(或系统)失去能量.
(四)多个力的总功的计算
法一:先求每个力做的功,再求代数和
W总=W1+W2+W3+······
注意:需要把各个功的正负号代入运算
法二:先求合力,再求总功
W总=F合lcosα
第七章 机械能守恒定律
第二节
一、新课引入
如图所示,木材被起重机举高,重力势能增加了;列车在机车的牵引下加速前进,动能增加了;用力压缩握力器后,握力器的弹性势能增加了。
现象:
思考:这些现象都有一个共同的特征,你能看出来吗?
木材在起重机的拉力作用下重力势能增加了
列车在机车牵引力作用下 动能增加了
握力器在手的压力作用下弹性势能增加了
物体的能量都发生了变化,
结论:
为了定量表达能量的变化,科学家引入功这个概念。
三、新课讲解
(一) 功的概念
如果一个物体受到力的作用, 并且在力的方向上发生了位移, 我们就说这个力对物体做了功.
案例说明
归纳:做功的两个必要条件
(1)作用在物体上的力.
(2)物体在力的方向发生一段位移
这两个条件是严格的,缺一不可 !
(二)功的表达式
1、力的方向与物体的运动方向一致
如右图所示物体在水平力F的作用下水平向右行驶的位移为l,则力F对物体所做的功为:
2、如果力的方向与运动方向垂直
如右图所示当力的方向跟位移方向垂直时,物体在力的方向上没有发生位移,力对物体不做功,即做功为零。 即
F
匀速运动
L
W=Fl
W = 0
3、当力的方向与位移方向成某一角度时
如右图所示物体m在与水平方向成α角的力F的作用下,沿水平方向向右行驶的距离为l,求力F对物体所做的功。
思路:
转化思想+
力或位移的 矢量性合矢量与两个分矢量等效
方法①
将位移l沿力方向和垂直于力方向分解如图所示,则沿力方向的位移l1=lcosα,垂直于力方向的位移l2=lsinα.
得出
方法②
将力F沿位移方向和垂直于位移方向分解如图所示,则沿位移方向的力F1=Fcosα,垂直于位移方向的力F2=Fsinα.
得出
W=Fl1=Flcosα.
W=F 1l =Fcosα l=Flcosα .
结论:力对物体做的功,等于这个力的大小、位移的大小、力和位移方
向夹角的余弦值的乘积,W=Flcosα.
①F是作用在物体上的力,必需是恒力,变力做功不能直接套用公式计算。
②l是物体发生的位移。
③α是F的方向和l的方向的夹角, 0~180°
④功是标量,只有大小没有方向。
特别提醒:
(三)功的正负
W=Flcosa
F
L
1、当α=0时,W =Fl
力F对物体做正功。
F
L
2、当α=π/2时,W =0
力F对物体没做功
F
L
3、当α<π/2时,W>0
力F对物体做正功。
F
L
4、当π/2 <α≤ π时,W <0
力F对物体做负功。
也叫做物体克服力F做功
意义 动力学角度 能 量 角 度
正功 力对物体做正功,这个力对物体来说是动力. 力对物体(或系统)做正功,外界向物体(或系统)提供能量,即正功表示受力物体(或系统)获得能量.
负功 力对物体做负功,这个力对物体来说是阻力. 力对物体(或系统)做负功,向外界输出能量,即负功表示物体(或系统)失去能量.
(四)多个力的总功的计算
法一:先求每个力做的功,再求代数和
W总=W1+W2+W3+······
注意:需要把各个功的正负号代入运算
法二:先求合力,再求总功
W总=F合lcosα
