人教版七年级数学下册 7.2.2坐标方法的简单应用 达标作业(解析版)
文档属性
| 名称 | 人教版七年级数学下册 7.2.2坐标方法的简单应用 达标作业(解析版) |
|
|
| 格式 | zip | ||
| 文件大小 | 168.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-02 09:29:52 | ||
图片预览



文档简介
7.2坐标方法的简单应用
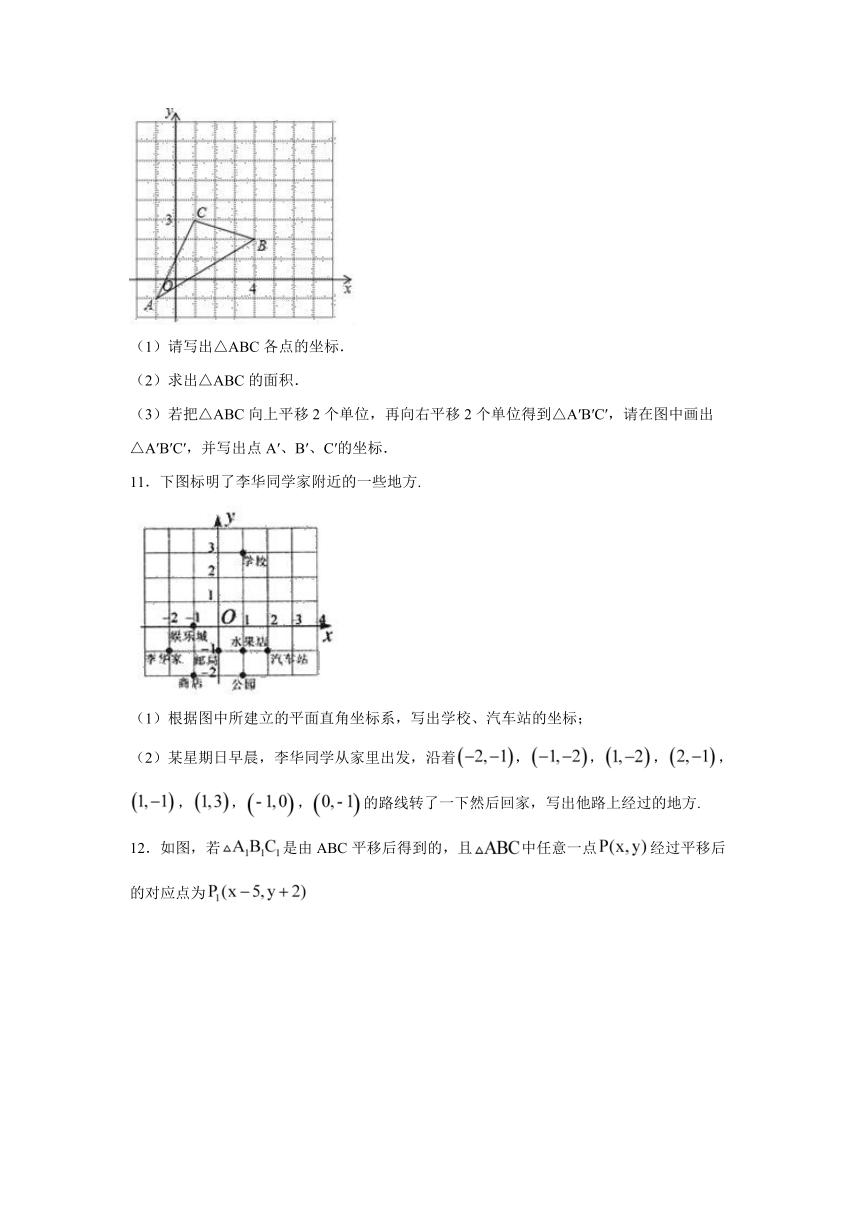
1.如图,在平面直角坐标系中,,,,,把一条长为2019个单位长度且没有弹性的细线线的粗细忽略不计的一端固定在点A处,并按的规律绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是
A. B. C. D.
2.在平面直角坐标系中,将点A(1,﹣2)向上平移3个单位长度,再向左平移2个单位长度,得到点A′,则点A′的坐标是( )
A.(﹣1,1) B.(﹣1,﹣2) C.(﹣1,2) D.(1,2)
3.在平面直角坐标系中,将点A(﹣1,﹣2)向右平移3个单位长度得到点B,则点B关于x轴的对称点B′的坐标为( )
A.(﹣3,﹣2) B.(2,2) C.(﹣2,2) D.(2,﹣2)
4.如图所示,点B在点O的东偏北30°,射线OB与射线OC所成的角是110°,则射线OC的方向是( )
A.北偏西30° B.北偏西40° C.北偏西50° D.西偏北50°
5.如图,的坐标为,,若将线段平移至,则的值为( )
A.5 B.4 C.3 D.2
6.在平面直角坐标系中,线段CF是由线段AB平移得到的:点A(﹣2,3)的对应点为C(1,2):则点B(a,b)的对应点F的坐标为( )
A.(a+3,b+1) B.(a+3,b﹣1) C.(a﹣3,b+1) D.(a﹣3,b﹣1)
7.在平面直角坐标系内,把,先向左平移2个单位长度,再向上平移4个单位长度后得到的点的坐标是_________.
8.如图,在平面直角坐标系中,点A(1,1),B(3,1),C(3,3),D(1,3),动点P从点A出发,以每秒1个单位长度的速度沿AB﹣BC﹣CD﹣DA﹣AB﹣…路线运动,当运动到2017秒时,点P的坐标为_____.
9.如图,A,B的坐标为(2,0),(0,1)若将线段AB平移至A1B1,则a+b的值为_____.
10.如图,△ABC在直角坐标系中,
(1)请写出△ABC各点的坐标.
(2)求出△ABC的面积.
(3)若把△ABC向上平移2个单位,再向右平移2个单位得到△A′B′C′,请在图中画出△A′B′C′,并写出点A′、B′、C′的坐标.
11.下图标明了李华同学家附近的一些地方.
(1)根据图中所建立的平面直角坐标系,写出学校、汽车站的坐标;
(2)某星期日早晨,李华同学从家里出发,沿着,,,,,,,的路线转了一下然后回家,写出他路上经过的地方.
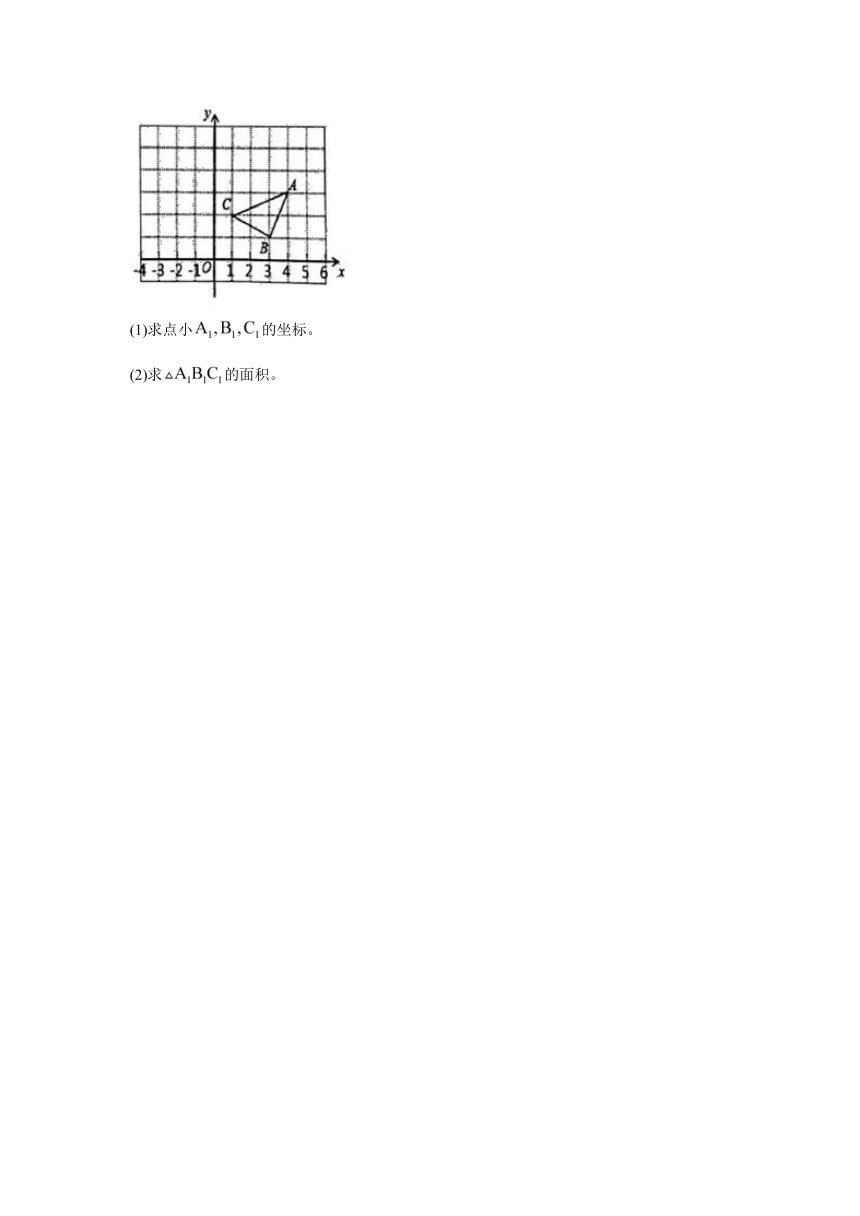
12.如图,若是由ABC平移后得到的,且中任意一点经过平移后的对应点为
(1)求点小的坐标。
(2)求的面积。
参考答案
1.C
【分析】
根据点的坐标求出四边形ABCD的周长,然后求出另一端是绕第几圈后的第几个单位长度,从而确定答案.
【详解】
∵A(1,1),B(﹣1,1),C(﹣1,﹣2),D(1,﹣2),
∴AB=1﹣(﹣1)=2,BC=1﹣(﹣2)=3,CD=1﹣(﹣1)=2,DA=1﹣(﹣2)=3,
∴绕四边形ABCD一周的细线长度为2+3+2+3=10,
2019÷10=201…9,
∴细线另一端在绕四边形第201圈的第9个单位长度的位置点的坐标为(1,0).
故选C.
【点睛】
本题利用点的坐标考查了数字变化规律,根据点的坐标求出四边形ABCD一周的长度,从而确定2019个单位长度的细线的另一端落在第几圈第几个单位长度的位置是解题的关键.
2.A
【解析】
试题分析:已知将点A(1,﹣2)向上平移3个单位长度,再向左平移2个单位长度,得到点A′,根据向左平移横坐标减,向上平移纵坐标加可得点A′的横坐标为1﹣2=﹣1,纵坐标为﹣2+3=1,即A′的坐标为(﹣1,1).故选A.
考点:坐标与图形变化-平移.
3.B
【分析】
首先根据横坐标右移加,左移减可得B点坐标,然后再根据关于x轴对称点的坐标特点:横坐标不变,纵坐标符号改变可得答案.
【详解】
点A(﹣1,﹣2)向右平移3个单位长度得到的B的坐标为(﹣1+3,﹣2),即(2,﹣2),则点B关于x轴的对称点B′的坐标是(2,2),故选B.
【点睛】
本题主要考查图形的平移和图形的轴对称,掌握点在直角坐标系中平移的特点以及点关于x轴对称点的特点是解答本题的关键.
4.C
【分析】
利用方向角的定义,结合图形分别判断得出答案即可.
【详解】
原图进行标注如下:
∵点B在点O的东偏北30°
∴∠BOA=30°
∵射线OB与射线OC所成的角是110°
∴∠BOC=110°
∴∠COE=180°-110°-30°=40°
∴∠COF=90°-40°=50°
即射线OC的方向是北偏西50°
故本题选C.
【点睛】
此题主要考查了方向角问题,利用方向角定义利用图形得出方向角是解题关键.
5.D
【分析】
平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.直接利用平移中点的变化规律求解即可.
【详解】
解:由B点平移前后的纵坐标分别为1、2,可得B点向上平移了1个单位,
由A点平移前后的横坐标分别是为2、3,可得A点向右平移了1个单位,
由此得线段AB的平移的过程是:向上平移1个单位,再向右平移1个单位,
所以点A、B均按此规律平移,
由此可得a=0+1=1,b=0+1=1,
故a+b=2.
故选D.
【点睛】
本题考查了坐标系中点、线段的平移规律,在平面直角坐标系中,图形的平移与图形上某点的平移相同.
6.B
【分析】
由题意:点A(﹣2,3)的对应点为C(1,2),推出点C是由点A向右平移3个单位,向下平移应该单位得到,由此即可解决问题.
【详解】
由题意:点A(﹣2,3)的对应点为C(1,2),
∴点C是由点A向右平移3个单位,向下平移应该单位得到,
∴点B(a,b)的对应点F的坐标为(a+3,b﹣1),
故选:B.
【点睛】
本题考查坐标与图形的性质,解题的关键是理解题意,灵活运用所学知识解决问题,属于中考常考题型.
7.(?7,2)
【分析】
直接利用平移中点的变化规律求解即可.平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.
【详解】
解:原来点的横坐标是?5,纵坐标是?2,向左平移2个单位长度,再向上平移4个单位得到新点的横坐标是?5?2=?7,纵坐标为?2+4=2.
得到的点的坐标是(?7,2).
故答案为:(?7,2).
【点睛】
本题考查图形的平移变换,关键是要懂得左右移动改变点的横坐标,左减,右加;上下移动改变点的纵坐标,下减,上加.
8.(2,1)
【分析】
由题意正方形ABCD的边长为2,周长为8,
由2017÷8=252余1,即可求解
【详解】
题意正方形ABCD的边长为2,周长为8,∵2017÷8=252余1,∴点P在AB上,PA=PB,∴P(2,1),故答案为(2,1).
【点睛】
本题是规律性问题,能根据题意确定出动点P最后的位置是关键.
9.2
【分析】
由图可得到点B的纵坐标是如何变化的,让A的纵坐标也做相应变化即可得到b的值;看点A的横坐标是如何变化的,让B的横坐标也做相应变化即可得到a的值,相加即可得到所求.
【详解】
解:由题意可知:a=0+(3﹣2)=1;b=0+(2﹣1)=1;
∴a+b=2.
故答案为:2.
【点睛】
本题考查了坐标平移,解决本题的关键是得到各点的平移规律.
10.(1)A(﹣1,﹣1),B(4,2),C(1,3);(2)S△ABC=7;(3)见解析,A′(1,1),B′(6,4),C′(3,5).
【解析】
【分析】
(1)根据各点在坐标系中的位置写出各点坐标即可;
(2)利用矩形的面积减去三个顶点上三角形的面积即可;
(3)根据图形平移的性质画出△A′B′C′,并写出点A′、B′、C′的坐标即可.
【详解】
解:(1)由图可知,A(﹣1,﹣1),B(4,2),C(1,3);
(2)S△ABC=4×5﹣×2×4﹣×1×3﹣×3×5
=7;
(3)如图,△A′B′C′即为所求,A′(1,1),B′(6,4),C′(3,5).
【点睛】
本题考查的是作图﹣平移变换,熟知图形平移不变性的性质是解答此题的关键.
11.(1)(1,3),(2,-1);(2)见解析.
【分析】
(1)根据原点的位置,直接可以得出学校,汽车站的坐标;
(2)根据点的坐标找出对应的地点,即可解决.
【详解】
(1)学校、汽车站的坐标分别为,;
(2)他路上经过的地方有:李华家,商店,公园,汽车站,水果店,学校,娱乐城,邮局.
【点睛】
此题主要考查了点的坐标确定方法以及由点的坐标确定位置,解决此类问题需要先确定原点的位置,再求未知点的位置,或者直接利用坐标系中的移动法则“右加左减,上加下减”来确定坐标.
12.(1)(-1,5),(-2,3),(-4,4);(2)三角形面积为2.5;
【分析】
(1)由△ABC中任意一点P(x,y)经平移后对应点为P1(x-5,y+2)可得△ABC的平移规律为:向左平移5个单位,向上平移2个单位,由此得到点A、B、C的对应点A1、B1、C1的坐标. (2)利用矩形的面积减去三个顶点上三角形的面积即可.
【详解】
解:(1)∵△ABC中任意一点P(x,y)经平移后对应点为P1(x-5,y+2), ∴△ABC的平移规律为:向左平移5个单位,向上平移2个单位, ∵A(4,3),B(3,1),C(1,2), ∴点A1的坐标为(-1,5),点B1的坐标为(-2,3),点C1的坐标为(-4,4). (2)如图所示, △A1B1C1的面积=3×2-×1×3-×1×2-×1×2=.
【点睛】
本题考查的是作图-平移变换,熟知图形平移不变性的性质是解答此题的关键.
1.如图,在平面直角坐标系中,,,,,把一条长为2019个单位长度且没有弹性的细线线的粗细忽略不计的一端固定在点A处,并按的规律绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是
A. B. C. D.
2.在平面直角坐标系中,将点A(1,﹣2)向上平移3个单位长度,再向左平移2个单位长度,得到点A′,则点A′的坐标是( )
A.(﹣1,1) B.(﹣1,﹣2) C.(﹣1,2) D.(1,2)
3.在平面直角坐标系中,将点A(﹣1,﹣2)向右平移3个单位长度得到点B,则点B关于x轴的对称点B′的坐标为( )
A.(﹣3,﹣2) B.(2,2) C.(﹣2,2) D.(2,﹣2)
4.如图所示,点B在点O的东偏北30°,射线OB与射线OC所成的角是110°,则射线OC的方向是( )
A.北偏西30° B.北偏西40° C.北偏西50° D.西偏北50°
5.如图,的坐标为,,若将线段平移至,则的值为( )
A.5 B.4 C.3 D.2
6.在平面直角坐标系中,线段CF是由线段AB平移得到的:点A(﹣2,3)的对应点为C(1,2):则点B(a,b)的对应点F的坐标为( )
A.(a+3,b+1) B.(a+3,b﹣1) C.(a﹣3,b+1) D.(a﹣3,b﹣1)
7.在平面直角坐标系内,把,先向左平移2个单位长度,再向上平移4个单位长度后得到的点的坐标是_________.
8.如图,在平面直角坐标系中,点A(1,1),B(3,1),C(3,3),D(1,3),动点P从点A出发,以每秒1个单位长度的速度沿AB﹣BC﹣CD﹣DA﹣AB﹣…路线运动,当运动到2017秒时,点P的坐标为_____.
9.如图,A,B的坐标为(2,0),(0,1)若将线段AB平移至A1B1,则a+b的值为_____.
10.如图,△ABC在直角坐标系中,
(1)请写出△ABC各点的坐标.
(2)求出△ABC的面积.
(3)若把△ABC向上平移2个单位,再向右平移2个单位得到△A′B′C′,请在图中画出△A′B′C′,并写出点A′、B′、C′的坐标.
11.下图标明了李华同学家附近的一些地方.
(1)根据图中所建立的平面直角坐标系,写出学校、汽车站的坐标;
(2)某星期日早晨,李华同学从家里出发,沿着,,,,,,,的路线转了一下然后回家,写出他路上经过的地方.
12.如图,若是由ABC平移后得到的,且中任意一点经过平移后的对应点为
(1)求点小的坐标。
(2)求的面积。
参考答案
1.C
【分析】
根据点的坐标求出四边形ABCD的周长,然后求出另一端是绕第几圈后的第几个单位长度,从而确定答案.
【详解】
∵A(1,1),B(﹣1,1),C(﹣1,﹣2),D(1,﹣2),
∴AB=1﹣(﹣1)=2,BC=1﹣(﹣2)=3,CD=1﹣(﹣1)=2,DA=1﹣(﹣2)=3,
∴绕四边形ABCD一周的细线长度为2+3+2+3=10,
2019÷10=201…9,
∴细线另一端在绕四边形第201圈的第9个单位长度的位置点的坐标为(1,0).
故选C.
【点睛】
本题利用点的坐标考查了数字变化规律,根据点的坐标求出四边形ABCD一周的长度,从而确定2019个单位长度的细线的另一端落在第几圈第几个单位长度的位置是解题的关键.
2.A
【解析】
试题分析:已知将点A(1,﹣2)向上平移3个单位长度,再向左平移2个单位长度,得到点A′,根据向左平移横坐标减,向上平移纵坐标加可得点A′的横坐标为1﹣2=﹣1,纵坐标为﹣2+3=1,即A′的坐标为(﹣1,1).故选A.
考点:坐标与图形变化-平移.
3.B
【分析】
首先根据横坐标右移加,左移减可得B点坐标,然后再根据关于x轴对称点的坐标特点:横坐标不变,纵坐标符号改变可得答案.
【详解】
点A(﹣1,﹣2)向右平移3个单位长度得到的B的坐标为(﹣1+3,﹣2),即(2,﹣2),则点B关于x轴的对称点B′的坐标是(2,2),故选B.
【点睛】
本题主要考查图形的平移和图形的轴对称,掌握点在直角坐标系中平移的特点以及点关于x轴对称点的特点是解答本题的关键.
4.C
【分析】
利用方向角的定义,结合图形分别判断得出答案即可.
【详解】
原图进行标注如下:
∵点B在点O的东偏北30°
∴∠BOA=30°
∵射线OB与射线OC所成的角是110°
∴∠BOC=110°
∴∠COE=180°-110°-30°=40°
∴∠COF=90°-40°=50°
即射线OC的方向是北偏西50°
故本题选C.
【点睛】
此题主要考查了方向角问题,利用方向角定义利用图形得出方向角是解题关键.
5.D
【分析】
平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.直接利用平移中点的变化规律求解即可.
【详解】
解:由B点平移前后的纵坐标分别为1、2,可得B点向上平移了1个单位,
由A点平移前后的横坐标分别是为2、3,可得A点向右平移了1个单位,
由此得线段AB的平移的过程是:向上平移1个单位,再向右平移1个单位,
所以点A、B均按此规律平移,
由此可得a=0+1=1,b=0+1=1,
故a+b=2.
故选D.
【点睛】
本题考查了坐标系中点、线段的平移规律,在平面直角坐标系中,图形的平移与图形上某点的平移相同.
6.B
【分析】
由题意:点A(﹣2,3)的对应点为C(1,2),推出点C是由点A向右平移3个单位,向下平移应该单位得到,由此即可解决问题.
【详解】
由题意:点A(﹣2,3)的对应点为C(1,2),
∴点C是由点A向右平移3个单位,向下平移应该单位得到,
∴点B(a,b)的对应点F的坐标为(a+3,b﹣1),
故选:B.
【点睛】
本题考查坐标与图形的性质,解题的关键是理解题意,灵活运用所学知识解决问题,属于中考常考题型.
7.(?7,2)
【分析】
直接利用平移中点的变化规律求解即可.平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.
【详解】
解:原来点的横坐标是?5,纵坐标是?2,向左平移2个单位长度,再向上平移4个单位得到新点的横坐标是?5?2=?7,纵坐标为?2+4=2.
得到的点的坐标是(?7,2).
故答案为:(?7,2).
【点睛】
本题考查图形的平移变换,关键是要懂得左右移动改变点的横坐标,左减,右加;上下移动改变点的纵坐标,下减,上加.
8.(2,1)
【分析】
由题意正方形ABCD的边长为2,周长为8,
由2017÷8=252余1,即可求解
【详解】
题意正方形ABCD的边长为2,周长为8,∵2017÷8=252余1,∴点P在AB上,PA=PB,∴P(2,1),故答案为(2,1).
【点睛】
本题是规律性问题,能根据题意确定出动点P最后的位置是关键.
9.2
【分析】
由图可得到点B的纵坐标是如何变化的,让A的纵坐标也做相应变化即可得到b的值;看点A的横坐标是如何变化的,让B的横坐标也做相应变化即可得到a的值,相加即可得到所求.
【详解】
解:由题意可知:a=0+(3﹣2)=1;b=0+(2﹣1)=1;
∴a+b=2.
故答案为:2.
【点睛】
本题考查了坐标平移,解决本题的关键是得到各点的平移规律.
10.(1)A(﹣1,﹣1),B(4,2),C(1,3);(2)S△ABC=7;(3)见解析,A′(1,1),B′(6,4),C′(3,5).
【解析】
【分析】
(1)根据各点在坐标系中的位置写出各点坐标即可;
(2)利用矩形的面积减去三个顶点上三角形的面积即可;
(3)根据图形平移的性质画出△A′B′C′,并写出点A′、B′、C′的坐标即可.
【详解】
解:(1)由图可知,A(﹣1,﹣1),B(4,2),C(1,3);
(2)S△ABC=4×5﹣×2×4﹣×1×3﹣×3×5
=7;
(3)如图,△A′B′C′即为所求,A′(1,1),B′(6,4),C′(3,5).
【点睛】
本题考查的是作图﹣平移变换,熟知图形平移不变性的性质是解答此题的关键.
11.(1)(1,3),(2,-1);(2)见解析.
【分析】
(1)根据原点的位置,直接可以得出学校,汽车站的坐标;
(2)根据点的坐标找出对应的地点,即可解决.
【详解】
(1)学校、汽车站的坐标分别为,;
(2)他路上经过的地方有:李华家,商店,公园,汽车站,水果店,学校,娱乐城,邮局.
【点睛】
此题主要考查了点的坐标确定方法以及由点的坐标确定位置,解决此类问题需要先确定原点的位置,再求未知点的位置,或者直接利用坐标系中的移动法则“右加左减,上加下减”来确定坐标.
12.(1)(-1,5),(-2,3),(-4,4);(2)三角形面积为2.5;
【分析】
(1)由△ABC中任意一点P(x,y)经平移后对应点为P1(x-5,y+2)可得△ABC的平移规律为:向左平移5个单位,向上平移2个单位,由此得到点A、B、C的对应点A1、B1、C1的坐标. (2)利用矩形的面积减去三个顶点上三角形的面积即可.
【详解】
解:(1)∵△ABC中任意一点P(x,y)经平移后对应点为P1(x-5,y+2), ∴△ABC的平移规律为:向左平移5个单位,向上平移2个单位, ∵A(4,3),B(3,1),C(1,2), ∴点A1的坐标为(-1,5),点B1的坐标为(-2,3),点C1的坐标为(-4,4). (2)如图所示, △A1B1C1的面积=3×2-×1×3-×1×2-×1×2=.
【点睛】
本题考查的是作图-平移变换,熟知图形平移不变性的性质是解答此题的关键.
