2020届高三数学高考冲刺:集合与不等式教案
文档属性
| 名称 | 2020届高三数学高考冲刺:集合与不等式教案 |  | |
| 格式 | zip | ||
| 文件大小 | 478.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-03 15:52:11 | ||
图片预览


文档简介
专题:集合与不等式综合(★★★)
教学目标
集合与不等式是高考数学命题的重要内容。
集合的考查主要有三个方面:一是集合的概念、关系和运算;二是集合语言与集合思想的运用(如求方程与不等式的解集、函数的定义域和值域等);三是命题之间的逻辑关系的判断和推理、此外与集合有关的信息迁移题、集合与其他知识相结合的综合题都值得高度关注。考查重点是集合与集合之间的关系、条件的判断。其核心考点有:集合的概念及相应关系,集合的运算,命题及充要条件。
不等式核心考点为不等式的性质与证明、不等式的解法(高频)和不等式的应用(利用不等式求最值(高频)).借助不等式的基本性质,考查函数方程思想、等价转化思想、数形结合思想及分类讨论思想等数学思想方法、含参数不等式的解法与讨论,不等式与函数、数列、三角等内容的综合问题,是高考命题的热点。
其中,集合与不等式相结合主要的考法有方程与不等式的解集问题、定义域值域问题、含参不等式等问题,这些都是高考考查的热点内容。
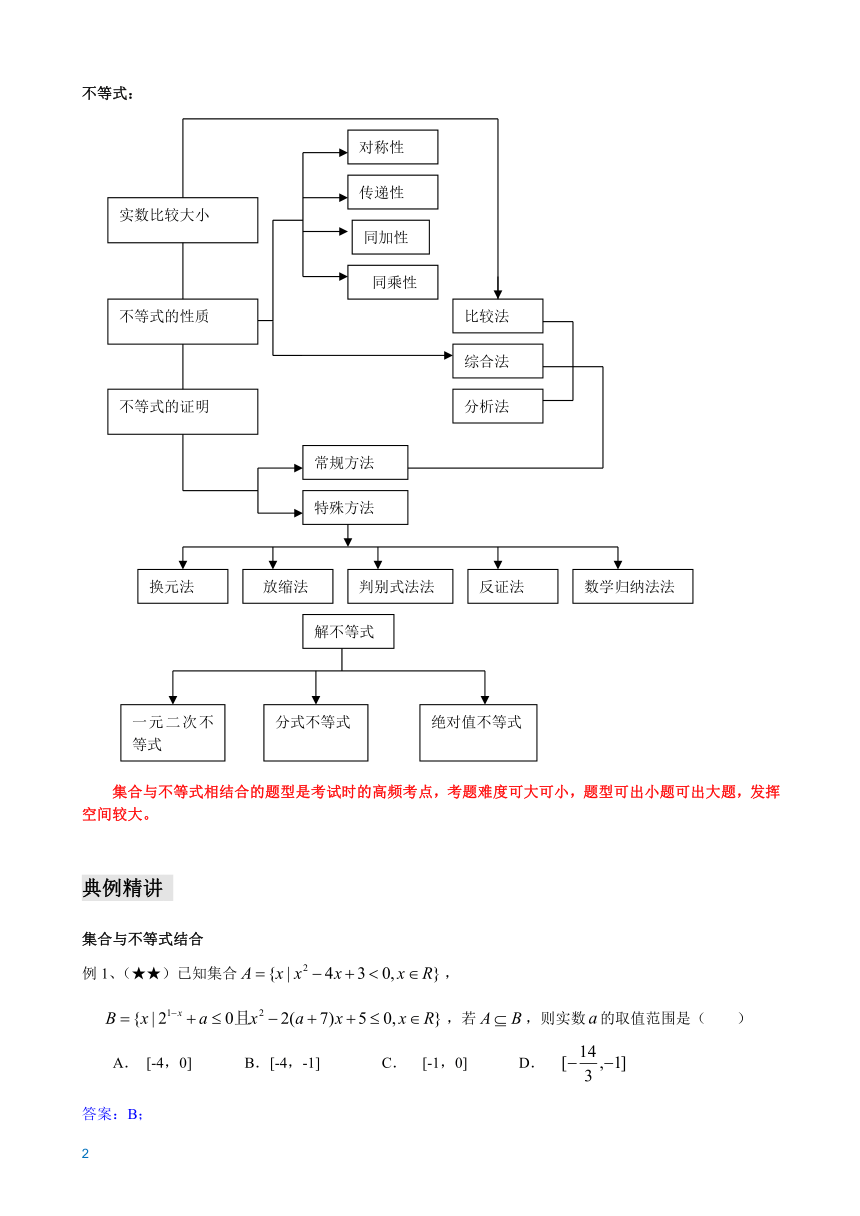
知识梳理
核心考点是集合的概念及相应关系,集合的运算,命题及充要条件。
不等式:
集合与不等式相结合的题型是考试时的高频考点,考题难度可大可小,题型可出小题可出大题,发挥空间较大。
典例精讲
集合与不等式结合
例1、(★★)已知集合,,若,则实数的取值范围是( )
A. [-4,0] B.[-4,-1] C. [-1,0] D.
答案:B;
例2、(★★★)已知集合A,B,若,
求实数的范围.
解:
例3、(★★★)求不等式解集:(1) ,(2) .
解析:(1)原不等式可化为:若时,解为,若时,
解为,若时,解为
(2). ①当.
方程有二实数根:
∴原不等式的解集为
①当时,,两根为
若则其根为-1,∴原不等式的解集为.
若则其根为1,∴原不等式的解集为.
②当时,方程无实数根.∴原不等式的解集为R.
分类讨论要注意讨论的标准始终如一,不能重复和遗漏。
巩固练习
1、(★★)已知全集,集合,,则= .
答案:;
2、(★★)已知集合,,则集合且_______.
答案:;
3、(★★)已知集合,则实数的取值范围是___
解答:
集合与方程综合
例4、(★★★)已知集合
(1)若A是空集,试求a的取值范围;
(2)若A中只有一个元素,求a的值,并把这个元素写出来;
(3)若A中至多只有一个元素,求a的取值范围.
解析 集合A是方程在实数范围内的解集.
(1)若A是空集,则显然,且方程无解,得,,即a的取值范围是.
(2)当时,,符合题意;当时,必须,,此时,符合题意;
综上所述,或.
(3) A中至多只有一个元素,包括A是空集和A中只有一个元素这两种情况,根据(1)和(2)的结果,知或,故a的取值范围是.
用分类讨论的方法解决集合中含参数的方程问题:
一般地,对于集合,其中,,均为实数,
当时,是一元二次方程的根的集合.须注意:若求非空集合中的元素之和,则应分与这两种情形,具体为
(1)若,则有两个不等的实根,于是,非空集合
中的元素之和为;
(2)若,则有两个相等的实根,于是,非空集合
中的元素之和为.
例5、(★★★)设,其中,如果,求实数a的取值范围.
解:,又,所以
(Ⅰ)时,
(Ⅱ)时,
(Ⅲ), 解得
∴综上所述实数 或
本题也可将0和-4带入集合B来解出a的值,但是要注意检验,同时要注意集合B为空集的情况。
巩固练习
1、(★★★)已知为单元素集,则实数的取值的集合为 .
.
本题是高频错题,错误原因是从到时没有注意方程是否完全等价,忘记了对原方程的类型进行讨论。
2、(★★★)设,求A中所有元素的和.
当时,和为;当时,和为-1.
3、(★★★)对于函数f(x),设,.
(1) 求证:;
(2) 若,且,求a的取值范围.
解: (1)略 (2) 提示:由知: ,中元素是方程的实根,由得方程要么没有实根,要么实根是方程的根,易得或,故的取值范围是.
根的分布问题
例6、(★★)若关于x的方程有一个正根和一个负根,则实数的取值范围是__________________.
一元二次方程根的分布问题是必须要掌握的内容,在复习时应根据学生情况将根的分布的几个基本类型都复习一遍。
巩固练习
1、(★★)若关于的二次方程有两个负实数根,则实数的取值
范围为 .
2、(★★)已知二次函数的图像在轴下方,则实数的取值范围为
.
回顾总结
1、一元一次不等式、一元二次不等的求解要正确、熟练、迅速,这是解分式不等式、无理不等式、指数不等式、对数不等式的基础 (?http:?/??/?www.xjktyg.com?/?wxc?/??) 带等号的分式不等式求解时,要注意分母不等于0,二次函数的值恒大于0的条件是且;若恒大于等于0,则且 (?http:?/??/?www.xjktyg.com?/?wxc?/??)若二次项系数中含参数且未指明该函 (?http:?/??/?www.xjktyg.com?/?wxc?/??)数是二次函数时,必须考虑二次项系数为0这一特殊情形。
2、忽略对定义域的考虑以及变形过程的不等价,是解无理不等式的常见错误,因此要强化对转化的依据的思考。
3、数形结合起来考虑,可以简化解题过程,特别是填空、选择题,还可利用图形验证,解题的结果。
4、解指数、对数不等式的过程中常用到换元法底数是参数时,须不重不漏地分类讨论。化同底是解不等式的前提。取对数也是解指数、对数不等式的常用方法之一,在取对数过程中,特别要注意必须考虑变量的取值范围。当所取对数的底数是字母时,随时要把“不等号是否变向”这一问题斟酌再三。
5、解含参数的不等式时,必须要注意参数的取值范围,并在此范围内对参数进行分类讨论。分类的标准要通过理解题意(例如能根据题意挖掘出题目的隐含条件),根据方法(例如利用单调性解题时,抓住使单调性发生变化的参数值),按照解答的需要(例如进行不等式变形时必须具备的变形条件)等方面来决定,要求做到不重复、不遗漏。
解不等式是不等式研究的主要内容,许多数学中的问题都可以转化为一个解不等式的问题,如函数的定义域、值域、最值和参数的取值范围,以及二次方程根的分布等 (?http:?/??/?www.xjktyg.com?/?wxc?/??)因此解不等式在数学中有着极其重要的地位,是高考的必考内容之一。
同加性
传递性
同乘性
对称性
不等式的性质
实数比较大小
不等式的证明
综合法
分析法
比较法
常规方法
特殊方法
换元法
放缩法
判别式法法
反证法
数学归纳法法
解不等式
一元二次不等式
绝对值不等式
分式不等式
PAGE
6
同课章节目录
