人教版九年级数学下册27.2.2相似三角形的性质 课件 (共24张PPT)
文档属性
| 名称 | 人教版九年级数学下册27.2.2相似三角形的性质 课件 (共24张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 924.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-02 13:26:17 | ||
图片预览





文档简介
(共24张PPT)
相似三角形的性质
(1)什么叫相似三角形?
对应角____、对应边成_____的三角形,叫做相似三角形.
(2)如何判定两个三角形相似?
①定义:____________________
②平行线分线段成比例定理推论:___________________
③三边___________________的两三角形相似。
④两个角_________________的两三角形相似。
⑤两边对应______,且______的两三角形相似。 ⑥直角三角形:______________________________
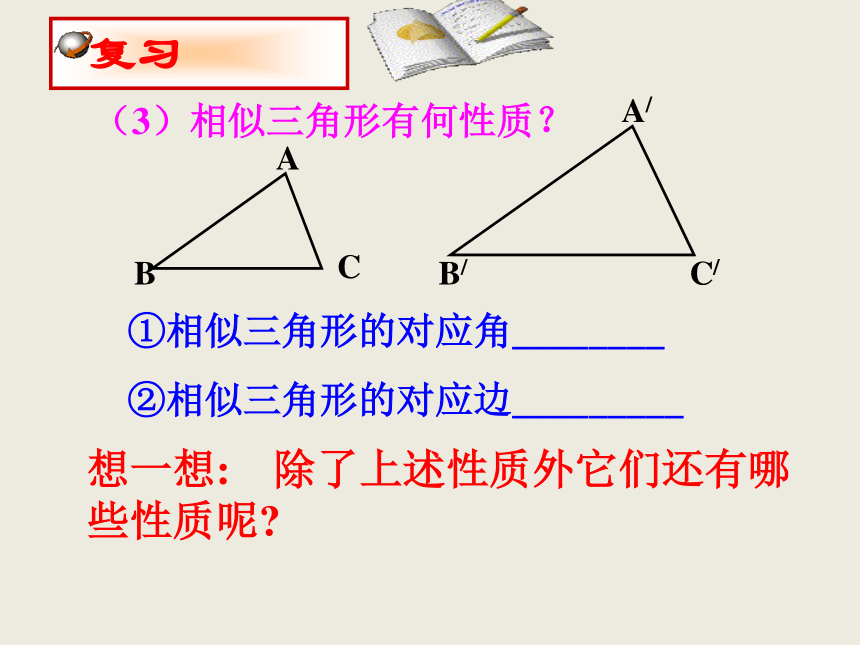
A
B
C
A/
B/
C/
①相似三角形的对应角________
②相似三角形的对应边_________
想一想: 除了上述性质外它们还有哪些性质呢?
(3)相似三角形有何性质?
(1)一个三角形有三条重要线段:
________________
(2)如果两个三角形相似,那么这些对应线段有什么关系呢?
合作交流学:
高线、?、?
思考下列问题:
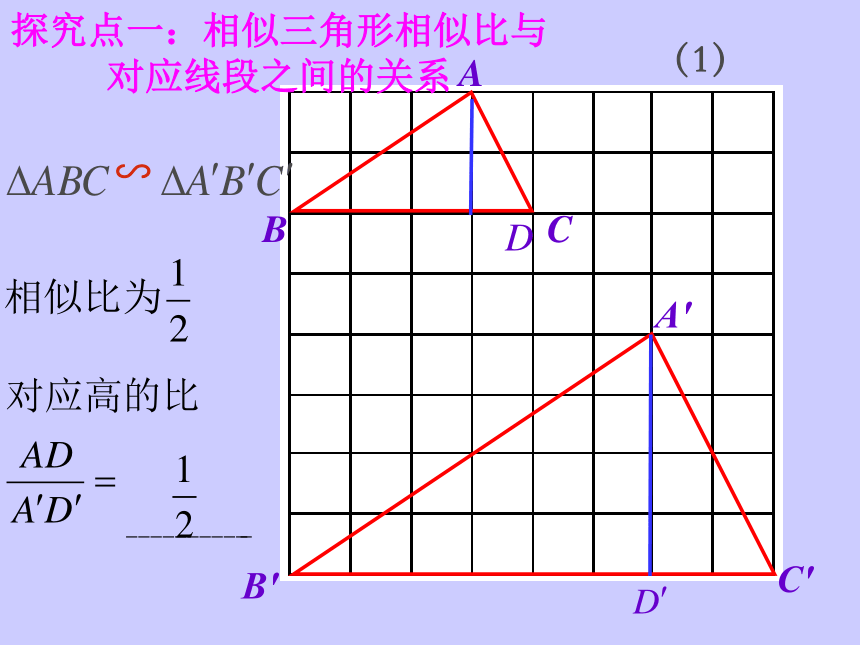
(1)
探究点一:相似三角形相似比与对应线段之间的关系
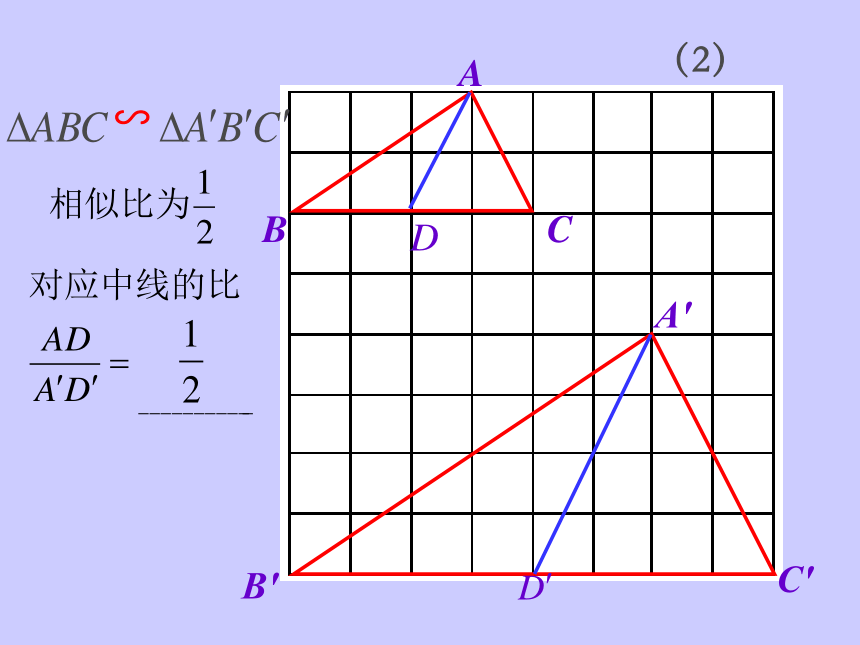
(2)
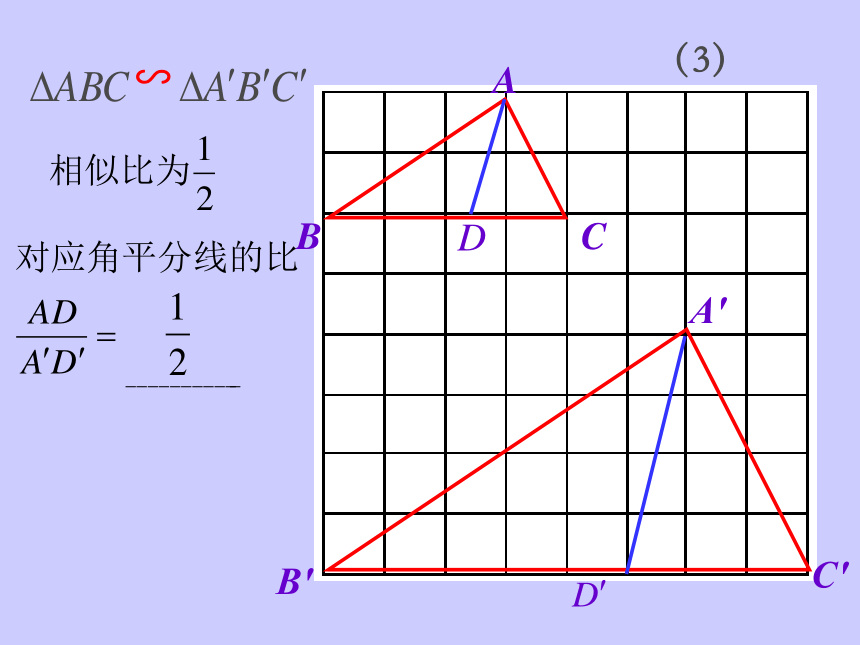
(3)
∽
可得:
观察这些数据,你会有怎样的猜想呢?
对应高的比
对应中线的比
对应角平分线的比
相
似
三
角
形
都等于相似比.
结论:相似三角形的性质
认真填一填:
1.相似三角形对应边的比为2∶3,那么相似比为_________,对应角的角平分线的比为______.
2.两个相似三角形的相似比为1:4, 则对应高的比为________,对应角的角平分线的比为_________.
3.两个相似三角形对应中线的比为 ,则相似比为___,对应高的比为_____.
4.判断题(见课本39页正上方第1题第一小题)
问题1:图中(1)(2)(3)分别是边长为1、2、3的等边三角形,它们都相似吗?
(1)
(2)
(3)
1
2
3
问题2:
(1)与(2)的相似比=____,周长比=___
(2)与(3)的相似比=____,周长比=___
探究点二:相似三角形相似比与周长比之间的关系
从数的角度去理解:
结论:相似三角形的周长比等于______.
相似比
1∶ 2
1∶ 2
2∶ 3
2∶ 3
已知△ABC∽△ ,且相似比为k。
求证:△ABC、 周长的比等于k
证明:
△ABC∽△
即△ABC、△ 的周长比等于相似比
∵
∴
∴
从形的角度去理解:
A
B
C
C'
A'
B'
总结:相似三角形的周长比等于______.
对应高的比
对应中线的比
对应角平分线的比
周长的比
相
似
三
角
形
都等于相似比.
相似三角形的性质
问题:两个相似三角形的面积
之间有什么关系呢?
相似三角形的性质
用心观察
1
2
3
1∶ 2
当相似比=k时,面积比=k2.
(1)
(2)
(3)
(1)与(2)的相似比=______,
(1)与(2)的面积比=______
(2)与(3)的相似比=______,
(2)与(3)的面积比=______
1∶ 4
2∶ 3
4∶ 9
相似三角形面积的比等于相似比的平方.
已知△ABC∽△ ,且相似比为k,AD、 分别是△ABC、△ 对应边BC、 上的高,求证:
证明:
∵△ABC∽△
∴
∴
从形的角度去理解:
结论:相似三角形面积的比等于__________
相似比的平方
对应高的比
对应中线的比
对应角平分线的比
周长的比
相
似
三
角
形
都等于相似比.
面积的比等于相似比的平方
相似三角形的性质
例3(课本38页): 已知△ABC∽ △DEF,AB=2DE,AC=2DF, ∠A=∠D,若△ABC的边BC边上的高为6,面积为12√5,求△DEF的边EF上的高和面积。
B
A
C
E
D
F
典例精析
(1)△ADE与△ABC相似吗?如果相似, 求它们的相似比。
A
B
C
D
E
(2) △ADE的周长︰△ABC的周长=____
1、如图,DE∥BC, DE = 1, BC = 4,
(4)
对点导练
____
2、思考并解决课本39页中的练习题。
1∶4
3:已知△ABC∽ △A?B ?C ?,BD和B ?D ?分别是△ABC和△A?B?C?中线,且AB=10,A?B?=2,BD=6。求B?D?的长。
解:∵ △ABC∽△A?B?C?
∴
=
=
B?D?=1.2
答:B?D?的长为1.2。
1、相似三角形对应边成____,对应角______.
2、相似三角形对应边上的高、对应边上的中线、
对应角平分线的比都等于________.
3、相似三角形周长的比等于________,
相似三角形面积的比等于______________.
课堂小结
相似比的平方
相似三角形的性质
相似多边形也有同样的结论
比例
相等
相似比
相似比
1.把一个三角形变成和它相似的三角形,
(1)如果边长扩大为原来的5倍,那么面积扩大为原来的______倍。
(2)如果面积扩大为原来的100倍,那么边长扩大为原来的______倍。
2、如图,在正方形网格上有△A1B1C1和△A2B2C2,这两个三角形相似吗? 如果相似,求出△A1B1C1和△A2B2C2的面积比.
3.如图,在 ABCD中,若E是AB的中点,则(1)?AEF与?CDF的相似比为______.(2)若?AEF的面积为5平方厘米,则?CDF的面积为______.
B
A
F
E
D
C
(第3题)
(3)若FGHI是正方形,它的边长是多少?你会把这个正方形剪出来吗?
课后思考:
4、如图,FG//BC,AE⊥FG,
AD⊥BC,E、D是垂足,FG=6,
BC=15,则(1)AE:AD是多少?
(2)若AD=10,求ED的长
再见!
相似三角形的性质
(1)什么叫相似三角形?
对应角____、对应边成_____的三角形,叫做相似三角形.
(2)如何判定两个三角形相似?
①定义:____________________
②平行线分线段成比例定理推论:___________________
③三边___________________的两三角形相似。
④两个角_________________的两三角形相似。
⑤两边对应______,且______的两三角形相似。 ⑥直角三角形:______________________________
A
B
C
A/
B/
C/
①相似三角形的对应角________
②相似三角形的对应边_________
想一想: 除了上述性质外它们还有哪些性质呢?
(3)相似三角形有何性质?
(1)一个三角形有三条重要线段:
________________
(2)如果两个三角形相似,那么这些对应线段有什么关系呢?
合作交流学:
高线、?、?
思考下列问题:
(1)
探究点一:相似三角形相似比与对应线段之间的关系
(2)
(3)
∽
可得:
观察这些数据,你会有怎样的猜想呢?
对应高的比
对应中线的比
对应角平分线的比
相
似
三
角
形
都等于相似比.
结论:相似三角形的性质
认真填一填:
1.相似三角形对应边的比为2∶3,那么相似比为_________,对应角的角平分线的比为______.
2.两个相似三角形的相似比为1:4, 则对应高的比为________,对应角的角平分线的比为_________.
3.两个相似三角形对应中线的比为 ,则相似比为___,对应高的比为_____.
4.判断题(见课本39页正上方第1题第一小题)
问题1:图中(1)(2)(3)分别是边长为1、2、3的等边三角形,它们都相似吗?
(1)
(2)
(3)
1
2
3
问题2:
(1)与(2)的相似比=____,周长比=___
(2)与(3)的相似比=____,周长比=___
探究点二:相似三角形相似比与周长比之间的关系
从数的角度去理解:
结论:相似三角形的周长比等于______.
相似比
1∶ 2
1∶ 2
2∶ 3
2∶ 3
已知△ABC∽△ ,且相似比为k。
求证:△ABC、 周长的比等于k
证明:
△ABC∽△
即△ABC、△ 的周长比等于相似比
∵
∴
∴
从形的角度去理解:
A
B
C
C'
A'
B'
总结:相似三角形的周长比等于______.
对应高的比
对应中线的比
对应角平分线的比
周长的比
相
似
三
角
形
都等于相似比.
相似三角形的性质
问题:两个相似三角形的面积
之间有什么关系呢?
相似三角形的性质
用心观察
1
2
3
1∶ 2
当相似比=k时,面积比=k2.
(1)
(2)
(3)
(1)与(2)的相似比=______,
(1)与(2)的面积比=______
(2)与(3)的相似比=______,
(2)与(3)的面积比=______
1∶ 4
2∶ 3
4∶ 9
相似三角形面积的比等于相似比的平方.
已知△ABC∽△ ,且相似比为k,AD、 分别是△ABC、△ 对应边BC、 上的高,求证:
证明:
∵△ABC∽△
∴
∴
从形的角度去理解:
结论:相似三角形面积的比等于__________
相似比的平方
对应高的比
对应中线的比
对应角平分线的比
周长的比
相
似
三
角
形
都等于相似比.
面积的比等于相似比的平方
相似三角形的性质
例3(课本38页): 已知△ABC∽ △DEF,AB=2DE,AC=2DF, ∠A=∠D,若△ABC的边BC边上的高为6,面积为12√5,求△DEF的边EF上的高和面积。
B
A
C
E
D
F
典例精析
(1)△ADE与△ABC相似吗?如果相似, 求它们的相似比。
A
B
C
D
E
(2) △ADE的周长︰△ABC的周长=____
1、如图,DE∥BC, DE = 1, BC = 4,
(4)
对点导练
____
2、思考并解决课本39页中的练习题。
1∶4
3:已知△ABC∽ △A?B ?C ?,BD和B ?D ?分别是△ABC和△A?B?C?中线,且AB=10,A?B?=2,BD=6。求B?D?的长。
解:∵ △ABC∽△A?B?C?
∴
=
=
B?D?=1.2
答:B?D?的长为1.2。
1、相似三角形对应边成____,对应角______.
2、相似三角形对应边上的高、对应边上的中线、
对应角平分线的比都等于________.
3、相似三角形周长的比等于________,
相似三角形面积的比等于______________.
课堂小结
相似比的平方
相似三角形的性质
相似多边形也有同样的结论
比例
相等
相似比
相似比
1.把一个三角形变成和它相似的三角形,
(1)如果边长扩大为原来的5倍,那么面积扩大为原来的______倍。
(2)如果面积扩大为原来的100倍,那么边长扩大为原来的______倍。
2、如图,在正方形网格上有△A1B1C1和△A2B2C2,这两个三角形相似吗? 如果相似,求出△A1B1C1和△A2B2C2的面积比.
3.如图,在 ABCD中,若E是AB的中点,则(1)?AEF与?CDF的相似比为______.(2)若?AEF的面积为5平方厘米,则?CDF的面积为______.
B
A
F
E
D
C
(第3题)
(3)若FGHI是正方形,它的边长是多少?你会把这个正方形剪出来吗?
课后思考:
4、如图,FG//BC,AE⊥FG,
AD⊥BC,E、D是垂足,FG=6,
BC=15,则(1)AE:AD是多少?
(2)若AD=10,求ED的长
再见!
