鲁教版(五四制)七年级数学下册第七章二元一次方程组复习课件(36张)
文档属性
| 名称 | 鲁教版(五四制)七年级数学下册第七章二元一次方程组复习课件(36张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-03 00:15:14 | ||
图片预览










文档简介
(共36张PPT)
二元一次方程组复习课件
二、有关二元一次方程概念
1.二元一次方程:通过化简后,只有两个未知数,并且两个未知数的次数都是1,系数都不是0的整式方程,叫做二元一次方程.
2.二元一次方程组:由两个一次方程组成,共有两个未知数的方程组,叫做二元一次方程组.
下列是二元一次方程组的是 ( )
B
什么是二元一次方程?
考点一:
m – n -1=1
m + n -7=1
8
考点二:解的定义
246
1.二元一次方程的每一个解是一对数值
2.二元一次方程有无数个解
3.二元一次方程组中各个方程的公共解,叫做这个二元一次方程组的解.
二元一次方程的解:
适合一个二元一次方程的一组未知数的值,叫做二元一次方程的一个解.
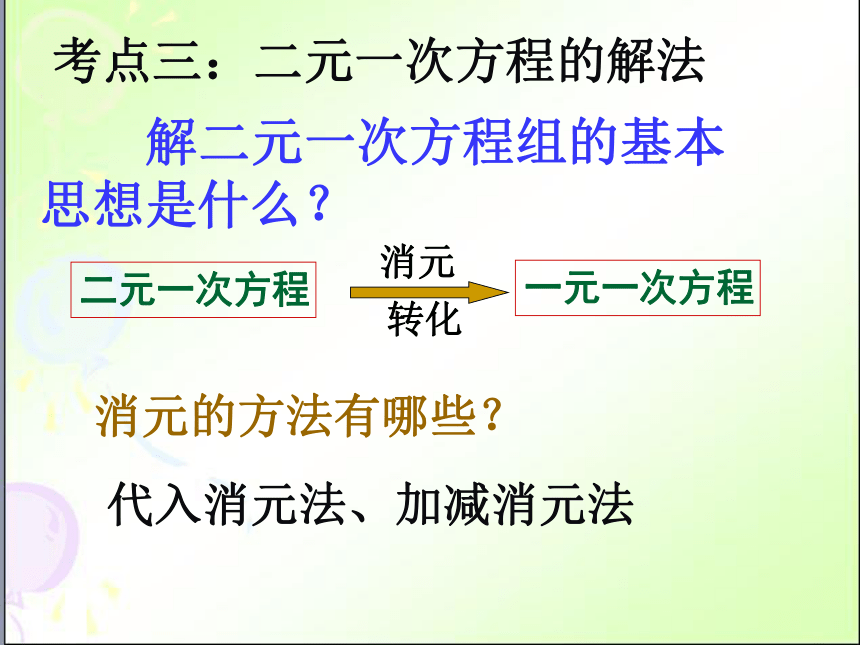
考点三:二元一次方程的解法
解二元一次方程组的基本思想是什么?
消元的方法有哪些?
代入消元法、加减消元法
1. 代入消元法
(1)有一个方程是:“用一个未知数的式子表示另一个未知数”的形式.
(2)方程组中某一未知数的系数是 1 或 -1.
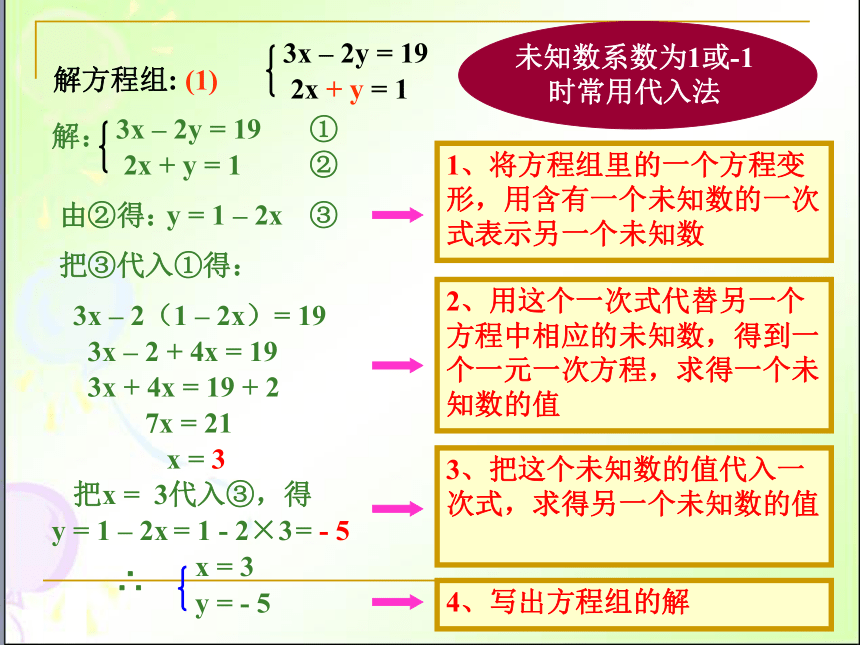
解方程组: (1)
解:
①
②
由②得:
y = 1 – 2x
③
把③代入①得:
3x – 2(1 – 2x)= 19
3x – 2 + 4x = 19
3x + 4x = 19 + 2
7x = 21
x = 3
把x = 3代入③,得
y = 1 – 2x
= 1 - 2×3
= - 5
∴
x = 3
y = - 5
1、将方程组里的一个方程变形,用含有一个未知数的一次式表示另一个未知数
2、用这个一次式代替另一个方程中相应的未知数,得到一个一元一次方程,求得一个未知数的值
3、把这个未知数的值代入一次式,求得另一个未知数的值
4、写出方程组的解
2. 加减消元法
(1)方程组中同一未知数的系数相等或相反数.
(2)方程组中同一未知数的系数是变成相同或相反数.
3x -2y= -8
2x +3y= 5
①
②
解:
①×2,得:
4x+6y=38 ③
②×3,得:
9x-6y=27 ④
③+④,得:
13x=65 x=5
把x=5代入①,得:
y=3
∴
思考:在例2中,你还能用什么方法解题?
(2).
加减法消元时,先要把相同未知数的系数化为相同或相反
1.解二元一次方程组的基本思路是
2.用加减法解方程组{ 由①与②
———— 直接消去——
3.用加减法解方程组{ 由
①与②——,可直接消去———
2x-5y=7①
2x+3y=2②
4x+5y=28①
6x-5y=12②
消元
相减
x
相加
y
A
5、方程2x+3y=8的解 ( )
A、只有一个 B、只有两个
C、只有三个 D、有无数个
6、下列属于二元一次方程组的是 ( )
A、 B
C、 x+y=5 D
x2+y2=1
D
A
7.方程组间接呈现形式举例如下:
已知 ︱4x+3y-5 ︱与 ︳x-3y-4 ︱互为相反数,求x、y之值。
已知 4x+3y-1 =x-3y=4 ,求x、y之值。
已知(4x+3y-5)2+ ︱x-3y-4︱=0,求x、y之值。
已知 3ay+5b3x与-5a2xb2-4y是同类项,求x、y之值。
11
一、行程问题
基本数量关系
路程=时间×速度
时间=路程/速度
速度=路程/时间
同时相向而行
路程=时间×速度之和
同时同向而行
路程=时间×速度之差
船在顺水中的速度=船在静水中的速度+水流的速度
船在逆水中的速度=船在静水中的速度-水流的速度
同时异地追及问题
乙的路程-甲的路程=甲乙之间的距离
例1.某站有甲、乙两辆汽车,若甲车先出发1h后乙车出发,则乙车出发后5h追上甲车;若甲车先开出30km后乙车出发,则乙车出发4h后乙车所走的路程比甲车所走路程多10km.求两车速度.
若甲车先出发1h后乙车出发,则乙车出发后5h追上甲车
解:设甲乙两车的速度分别为
x Km/h、y Km/h
根据题意,得
5y=6x
若甲车先开出30km后乙车出发,则乙车出发4h后乙车所走的路程比甲车所走路程多10km.
4y=4x+40
解之得
答:甲乙两车的速度分别为50km、60km
有大小两种货车,2辆大车与3辆小车
一次可以运货15.50吨,5辆大车与6辆小
车一次可以运货35吨。
求:3辆大车与3辆小车一次可以运货
多少吨?
列方程组解应用题的基本步骤:
1、审题,设未知数。
2、找等量关系。
3、列出方程组,并解答。
4、检验并答。
3、 已知一个两位数,十位数字比
个位数字大3 ,将十位数字与个位
数字对调所得的新数比原数小27,
求这个两位数。
若设十位数字为x,个位数字为y,则
x
y
10x+y
y
x
10y+x
十位 个位 三位数的代数式
原数
新数
四、配套问题
(一)配套与人员分配问题
例1.某车间22名工人生产螺钉与螺母,每人每天平均生产螺钉1200个或螺母2000个,一个螺钉要配两个螺母,为了使每天生产的产品刚好配套,应该分配多少名工人生产螺钉,多少名工人生产螺母?
一个螺钉配两个螺母
螺钉数:螺母数=1:2
解:设分配名x工人生产螺钉,y名工人生产螺母,则一天生产的螺钉数为1200x个,生产的螺母数为2000y个.
所以为了使每天生产的产品刚好配套,应安排10人生产螺钉,12人生产螺母
练习.一张方桌由1 个桌面、4条桌腿组成,如果1立方米木料可以做方桌的桌面50个,或桌腿300条,现有5立方米的木料,那么用多少立方米木料做桌面、多少立方米木料做桌腿,做出的桌面和桌腿恰好配成方桌?能配成 多少方桌?
解:设用x立方米做桌面,y立方米做桌腿,则可以做桌面50x个,做桌腿300y条
所以用3立方米做桌面 ,2立方米做桌腿,恰能配成方桌,共可做成150张方桌。
某企业接到任务,须在规定时间内生产一批防护服.如果按原来的生产速度,每天生产120套,那么在规定时间内只能完成任务的90%.为按时完成任务,该企业所有人员都支援到生产第一线,这样,每天能生产160套,刚好提前一天完成任务.问规定时间是多少天?生产任务是多少套防护服?
用加减法解二元一次方程组
解方程组:
二元一次方程组复习课件
二、有关二元一次方程概念
1.二元一次方程:通过化简后,只有两个未知数,并且两个未知数的次数都是1,系数都不是0的整式方程,叫做二元一次方程.
2.二元一次方程组:由两个一次方程组成,共有两个未知数的方程组,叫做二元一次方程组.
下列是二元一次方程组的是 ( )
B
什么是二元一次方程?
考点一:
m – n -1=1
m + n -7=1
8
考点二:解的定义
246
1.二元一次方程的每一个解是一对数值
2.二元一次方程有无数个解
3.二元一次方程组中各个方程的公共解,叫做这个二元一次方程组的解.
二元一次方程的解:
适合一个二元一次方程的一组未知数的值,叫做二元一次方程的一个解.
考点三:二元一次方程的解法
解二元一次方程组的基本思想是什么?
消元的方法有哪些?
代入消元法、加减消元法
1. 代入消元法
(1)有一个方程是:“用一个未知数的式子表示另一个未知数”的形式.
(2)方程组中某一未知数的系数是 1 或 -1.
解方程组: (1)
解:
①
②
由②得:
y = 1 – 2x
③
把③代入①得:
3x – 2(1 – 2x)= 19
3x – 2 + 4x = 19
3x + 4x = 19 + 2
7x = 21
x = 3
把x = 3代入③,得
y = 1 – 2x
= 1 - 2×3
= - 5
∴
x = 3
y = - 5
1、将方程组里的一个方程变形,用含有一个未知数的一次式表示另一个未知数
2、用这个一次式代替另一个方程中相应的未知数,得到一个一元一次方程,求得一个未知数的值
3、把这个未知数的值代入一次式,求得另一个未知数的值
4、写出方程组的解
2. 加减消元法
(1)方程组中同一未知数的系数相等或相反数.
(2)方程组中同一未知数的系数是变成相同或相反数.
3x -2y= -8
2x +3y= 5
①
②
解:
①×2,得:
4x+6y=38 ③
②×3,得:
9x-6y=27 ④
③+④,得:
13x=65 x=5
把x=5代入①,得:
y=3
∴
思考:在例2中,你还能用什么方法解题?
(2).
加减法消元时,先要把相同未知数的系数化为相同或相反
1.解二元一次方程组的基本思路是
2.用加减法解方程组{ 由①与②
———— 直接消去——
3.用加减法解方程组{ 由
①与②——,可直接消去———
2x-5y=7①
2x+3y=2②
4x+5y=28①
6x-5y=12②
消元
相减
x
相加
y
A
5、方程2x+3y=8的解 ( )
A、只有一个 B、只有两个
C、只有三个 D、有无数个
6、下列属于二元一次方程组的是 ( )
A、 B
C、 x+y=5 D
x2+y2=1
D
A
7.方程组间接呈现形式举例如下:
已知 ︱4x+3y-5 ︱与 ︳x-3y-4 ︱互为相反数,求x、y之值。
已知 4x+3y-1 =x-3y=4 ,求x、y之值。
已知(4x+3y-5)2+ ︱x-3y-4︱=0,求x、y之值。
已知 3ay+5b3x与-5a2xb2-4y是同类项,求x、y之值。
11
一、行程问题
基本数量关系
路程=时间×速度
时间=路程/速度
速度=路程/时间
同时相向而行
路程=时间×速度之和
同时同向而行
路程=时间×速度之差
船在顺水中的速度=船在静水中的速度+水流的速度
船在逆水中的速度=船在静水中的速度-水流的速度
同时异地追及问题
乙的路程-甲的路程=甲乙之间的距离
例1.某站有甲、乙两辆汽车,若甲车先出发1h后乙车出发,则乙车出发后5h追上甲车;若甲车先开出30km后乙车出发,则乙车出发4h后乙车所走的路程比甲车所走路程多10km.求两车速度.
若甲车先出发1h后乙车出发,则乙车出发后5h追上甲车
解:设甲乙两车的速度分别为
x Km/h、y Km/h
根据题意,得
5y=6x
若甲车先开出30km后乙车出发,则乙车出发4h后乙车所走的路程比甲车所走路程多10km.
4y=4x+40
解之得
答:甲乙两车的速度分别为50km、60km
有大小两种货车,2辆大车与3辆小车
一次可以运货15.50吨,5辆大车与6辆小
车一次可以运货35吨。
求:3辆大车与3辆小车一次可以运货
多少吨?
列方程组解应用题的基本步骤:
1、审题,设未知数。
2、找等量关系。
3、列出方程组,并解答。
4、检验并答。
3、 已知一个两位数,十位数字比
个位数字大3 ,将十位数字与个位
数字对调所得的新数比原数小27,
求这个两位数。
若设十位数字为x,个位数字为y,则
x
y
10x+y
y
x
10y+x
十位 个位 三位数的代数式
原数
新数
四、配套问题
(一)配套与人员分配问题
例1.某车间22名工人生产螺钉与螺母,每人每天平均生产螺钉1200个或螺母2000个,一个螺钉要配两个螺母,为了使每天生产的产品刚好配套,应该分配多少名工人生产螺钉,多少名工人生产螺母?
一个螺钉配两个螺母
螺钉数:螺母数=1:2
解:设分配名x工人生产螺钉,y名工人生产螺母,则一天生产的螺钉数为1200x个,生产的螺母数为2000y个.
所以为了使每天生产的产品刚好配套,应安排10人生产螺钉,12人生产螺母
练习.一张方桌由1 个桌面、4条桌腿组成,如果1立方米木料可以做方桌的桌面50个,或桌腿300条,现有5立方米的木料,那么用多少立方米木料做桌面、多少立方米木料做桌腿,做出的桌面和桌腿恰好配成方桌?能配成 多少方桌?
解:设用x立方米做桌面,y立方米做桌腿,则可以做桌面50x个,做桌腿300y条
所以用3立方米做桌面 ,2立方米做桌腿,恰能配成方桌,共可做成150张方桌。
某企业接到任务,须在规定时间内生产一批防护服.如果按原来的生产速度,每天生产120套,那么在规定时间内只能完成任务的90%.为按时完成任务,该企业所有人员都支援到生产第一线,这样,每天能生产160套,刚好提前一天完成任务.问规定时间是多少天?生产任务是多少套防护服?
用加减法解二元一次方程组
解方程组:
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
