人教版七年级数学下册 5.1.1 相交线 导学案(无答案)
文档属性
| 名称 | 人教版七年级数学下册 5.1.1 相交线 导学案(无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 306.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-02 00:00:00 | ||
图片预览

文档简介
第5章 相交线和平行线
第1课时 相交线
学习目标:
1.理解对顶角、邻补角的概念;
2.探索并掌握对顶角相等的性质.
学习重点:
对顶角的性质.
学习难点:
对顶角相等性质的证明.
一、复习回顾
1.平面中不重合的两条直线的位置关系_______和_______.
列举生活中有相交线和平行线形象的例子.
2、探索新知
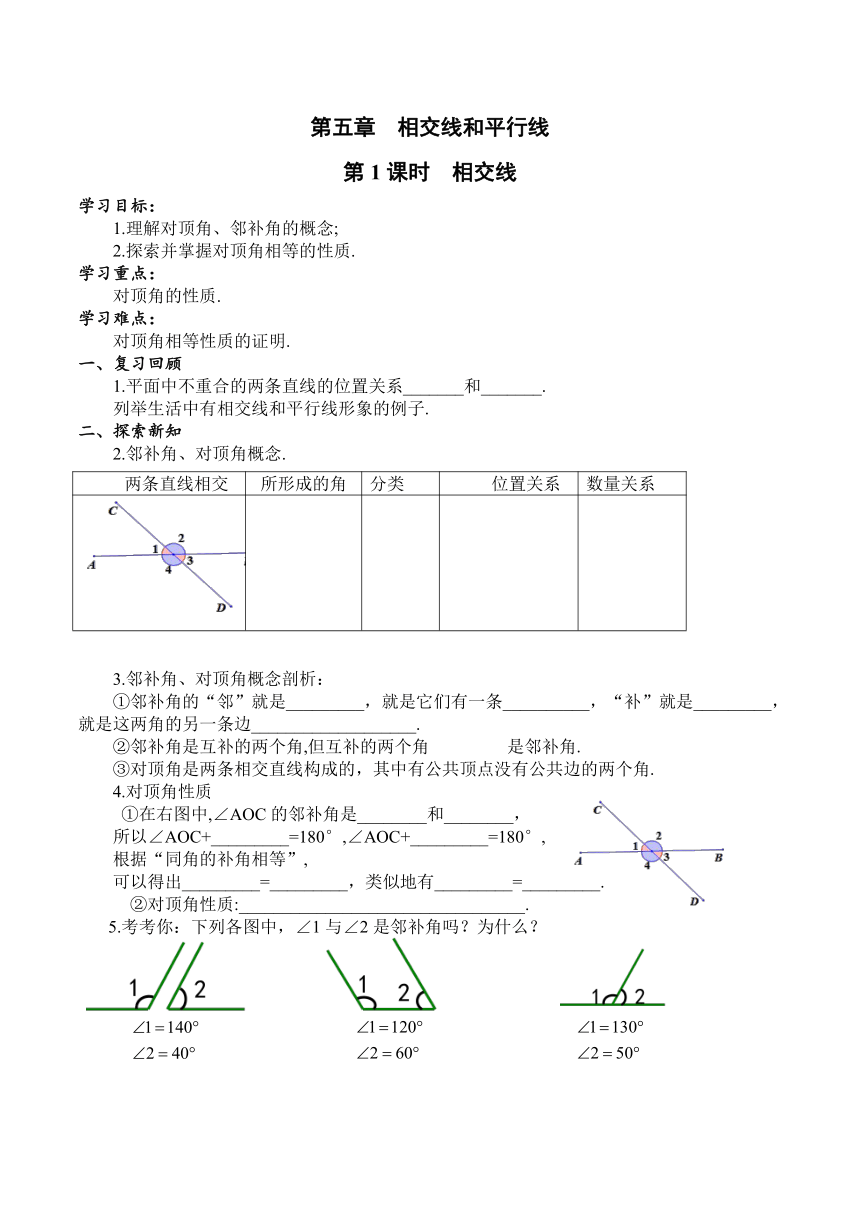
2.邻补角、对顶角概念.
两条直线相交 所形成的角 分类 位置关系 数量关系
3.邻补角、对顶角概念剖析:
①邻补角的“邻”就是_________,就是它们有一条__________,“补”就是_________,就是这两角的另一条边___________________.
②邻补角是互补的两个角,但互补的两个角 是邻补角.
③对顶角是两条相交直线构成的,其中有公共顶点没有公共边的两个角.
4.对顶角性质
①在右图中,∠AOC的邻补角是________和________,
所以∠AOC+_________=180°,∠AOC+_________=180°,
根据“同角的补角相等”,
可以得出_________=_________,类似地有_________=_________.
②对顶角性质:_________________________________.
5.考考你:下列各图中,∠1与∠2是邻补角吗?为什么?
6.考考你:下列各图中,∠1与∠2是对顶角的是( ).
三、例题解析
例1 如图,直线AB,CD相交,∠1=40°,求∠2,∠3,∠4的度数.
变式1:若则_______,_______.
变式2:若∠2是∠1的3倍,求∠3的度数.
四、课后练习
1. 若∠1与∠2是对顶角,∠1=160,则∠2=______°;
若∠3与∠4是邻补角,则∠3+∠4 =______°.
2.若∠1与∠2为对顶角,∠1与∠3互补,则∠2+∠3= °.
3.图中是对顶角量角器,你能说出用它测量角的原理吗?
4.如图1,直线AB、CD相交于O,OE是射线.则
∠3的对顶角是_____________, ∠1的对顶角是_____________,
∠1的邻补角是_____________,∠2的邻补角是_____________.
5.如图2,∠2与∠3为邻补角,∠1=∠2,则∠1与∠3的关系为 .
6.已知两条直线相交成的四个角,其中一个角是90°,其余各角是___________.
7.如图3,三条直线a,b,c相交于点O,∠1=40°,∠2=55°,则∠3=_____.
8.如图两堵墙围一个角AOB,但人不能进入围墙,我们如何去测量这个角的大小呢?
9.如图,已知直线AB,CD相交于点O,OA平分∠EOC,∠EOC=70°,求∠BOD,∠BOC的度数.
图1
图2
图3
A
B
O
第1课时 相交线
学习目标:
1.理解对顶角、邻补角的概念;
2.探索并掌握对顶角相等的性质.
学习重点:
对顶角的性质.
学习难点:
对顶角相等性质的证明.
一、复习回顾
1.平面中不重合的两条直线的位置关系_______和_______.
列举生活中有相交线和平行线形象的例子.
2、探索新知
2.邻补角、对顶角概念.
两条直线相交 所形成的角 分类 位置关系 数量关系
3.邻补角、对顶角概念剖析:
①邻补角的“邻”就是_________,就是它们有一条__________,“补”就是_________,就是这两角的另一条边___________________.
②邻补角是互补的两个角,但互补的两个角 是邻补角.
③对顶角是两条相交直线构成的,其中有公共顶点没有公共边的两个角.
4.对顶角性质
①在右图中,∠AOC的邻补角是________和________,
所以∠AOC+_________=180°,∠AOC+_________=180°,
根据“同角的补角相等”,
可以得出_________=_________,类似地有_________=_________.
②对顶角性质:_________________________________.
5.考考你:下列各图中,∠1与∠2是邻补角吗?为什么?
6.考考你:下列各图中,∠1与∠2是对顶角的是( ).
三、例题解析
例1 如图,直线AB,CD相交,∠1=40°,求∠2,∠3,∠4的度数.
变式1:若则_______,_______.
变式2:若∠2是∠1的3倍,求∠3的度数.
四、课后练习
1. 若∠1与∠2是对顶角,∠1=160,则∠2=______°;
若∠3与∠4是邻补角,则∠3+∠4 =______°.
2.若∠1与∠2为对顶角,∠1与∠3互补,则∠2+∠3= °.
3.图中是对顶角量角器,你能说出用它测量角的原理吗?
4.如图1,直线AB、CD相交于O,OE是射线.则
∠3的对顶角是_____________, ∠1的对顶角是_____________,
∠1的邻补角是_____________,∠2的邻补角是_____________.
5.如图2,∠2与∠3为邻补角,∠1=∠2,则∠1与∠3的关系为 .
6.已知两条直线相交成的四个角,其中一个角是90°,其余各角是___________.
7.如图3,三条直线a,b,c相交于点O,∠1=40°,∠2=55°,则∠3=_____.
8.如图两堵墙围一个角AOB,但人不能进入围墙,我们如何去测量这个角的大小呢?
9.如图,已知直线AB,CD相交于点O,OA平分∠EOC,∠EOC=70°,求∠BOD,∠BOC的度数.
图1
图2
图3
A
B
O
