人教版九年级数学下册26.1 :反比例函数 同步练习(含答案)
文档属性
| 名称 | 人教版九年级数学下册26.1 :反比例函数 同步练习(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 206.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-02 12:59:38 | ||
图片预览


文档简介
反比例函数 同步练习
1、选择题
1、下列函数,①y=2x,②y=x,③y=x-1,④y=是反比例函数的个数有(? )
A.0个??? B.1个??? C.2个??? D.3个
2、反比例函数y=的图象位于(? )
A.第一、二象限??? B.第一、三象限??? C.第二、三象限??? D.第二、四象限
3、关于反比例函数y=的图象,下列说法正确的是( )
A.必经过点(1,1) B.两个分支分布在第二、四象限
C.两个分支关于x轴成轴对称 D.两个分支关于原点成中心对称
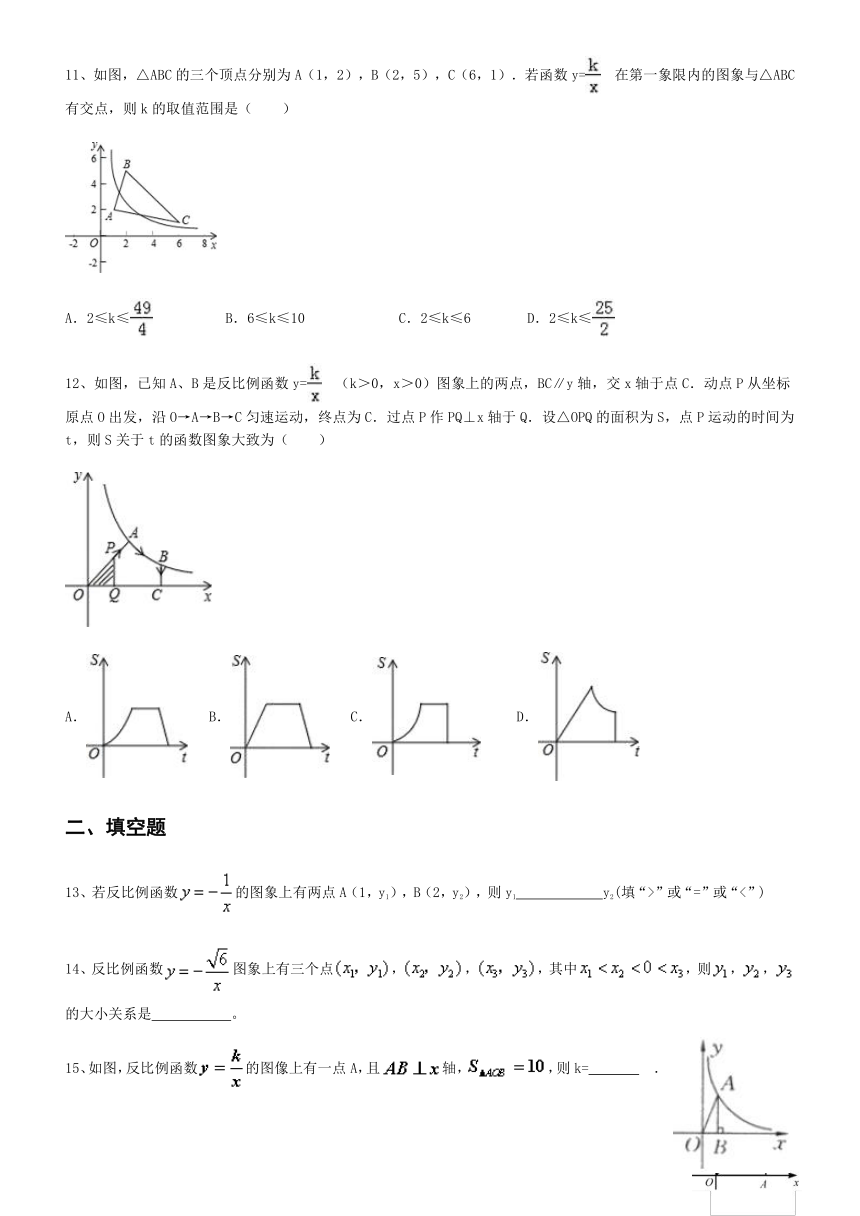
4、已知矩形的面积为10,则它的长y与宽x之间的关系用图象表示大致为(? )
5、如图,过反比例函数y=(x>0)的图象上一点A作AB⊥x轴于点B,连接AO,若S△AOB=2,则k的值为( )
A.2???? B.3????? C.4???? D.5
6、.如图,A,B两点在反比例函数y=的图象上,C,D两点在反比例函数y=的图象上,AC⊥y轴于点E,BD⊥y轴于点F,AC=2,BD=1,EF=3,则k1-k2的值是( ??)
A.6? B.4? C.3 ? D.2
7、如图,在平面直角坐标系中,?OABC的顶点A的坐标为(-4,0),顶点B在第二象限,∠BAO=60°,BC交y轴于点D,DB∶DC=3∶1.若函数y=(k>0,x>0)的图象经过点C,则k的值为( ?)
A.? B.? C. ? D.
8、如图,点A在双曲线y=上,点B在双曲线y=(k≠0)上,AB∥x轴,分别过点A,B向x轴作垂线,垂足分别为D,C,若矩形ABCD的面积是8,则k的值为( ?)
A.12? B.10? C.8? D.6
9、如图,正比例函数y1=k1x的图象与反比例函数y2=的图象相交于A,B两点,其中点A的横坐标为2,当y1>y2时,x的取值范围是( ?)
A.x<-2或x>2? B.x<-2或0<x<2
C.-2<x<0或0<x<-2? D.-2<x<0或x>2
10、一次函数y=ax+a(a为常数,a≠0)与反比例函数y=(a为常数,a≠0)在同一平面直角坐标系内的图象大致为( ?)
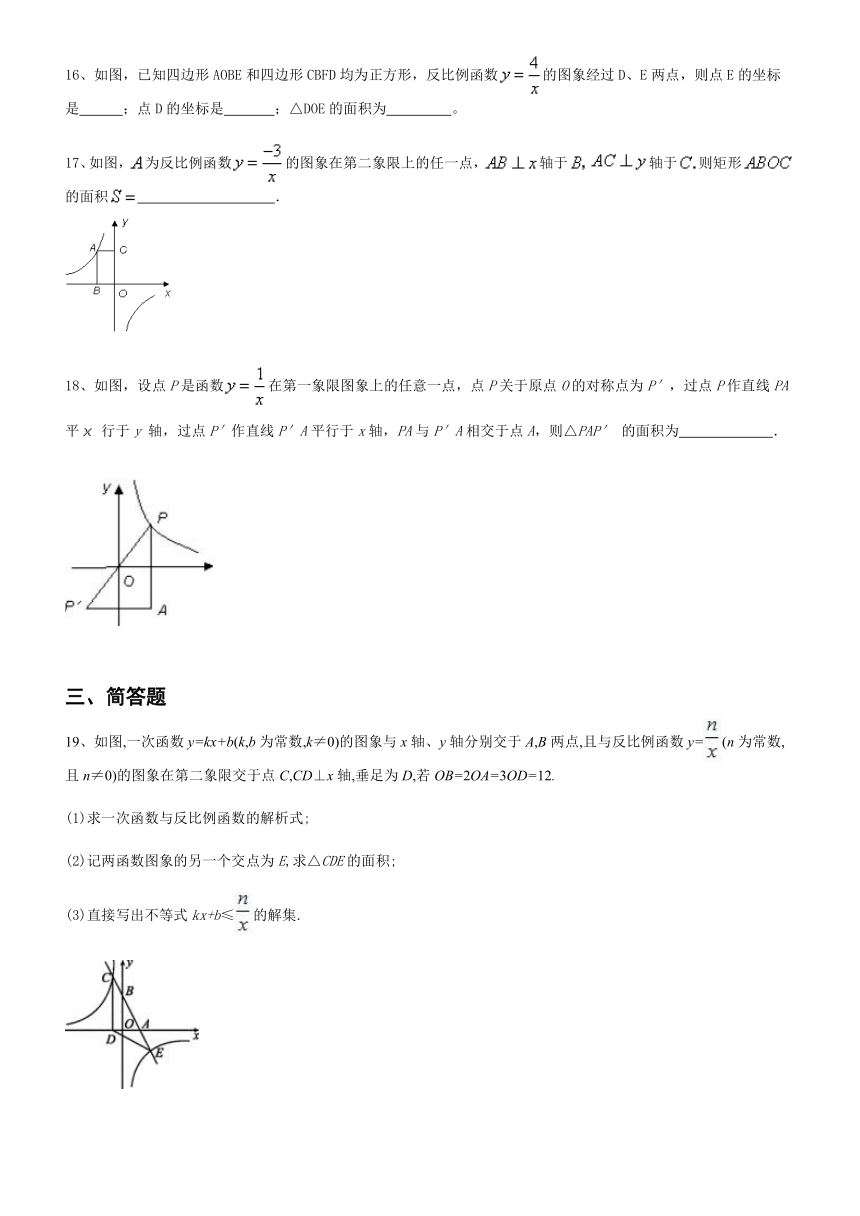
11、如图,△ABC的三个顶点分别为A(1,2),B(2,5),C(6,1).若函数y=在第一象限内的图象与△ABC有交点,则k的取值范围是( )
A.2≤k≤??? B.6≤k≤10 C.2≤k≤6? D.2≤k≤
12、如图,已知A、B是反比例函数y=(k>0,x>0)图象上的两点,BC∥y轴,交x轴于点C.动点P从坐标原点O出发,沿O→A→B→C匀速运动,终点为C.过点P作PQ⊥x轴于Q.设△OPQ的面积为S,点P运动的时间为t,则S关于t的函数图象大致为( )
A.? B.? C.?? D.
二、填空题
13、若反比例函数的图象上有两点A(1,y1),B(2,y2),则y1??????y2(填“>”或“=”或“<”)??
14、反比例函数图象上有三个点,,,其中,则,,的大小关系是????? 。
15、如图,反比例函数的图像上有一点A,且轴,,则k=??? ?.
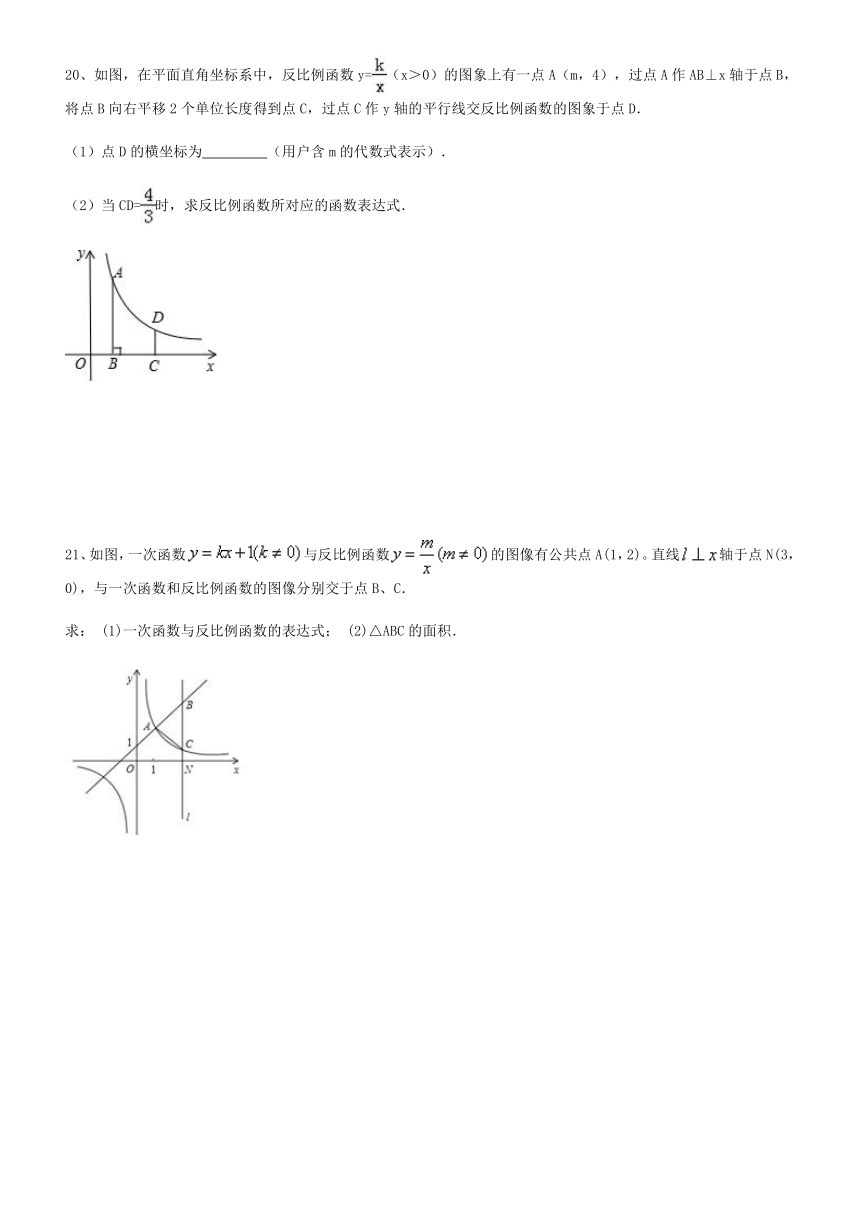
16、如图,已知四边形AOBE和四边形CBFD均为正方形,反比例函数的图象经过D、E两点,则点E的坐标是 ?;点D的坐标是 ?;△DOE的面积为??? 。
17、如图,为反比例函数的图象在第二象限上的任一点,轴于轴于则矩形的面积??????? ??.
18、如图,设点P是函数在第一象限图象上的任意一点,点P关于原点O的对称点为P′,过点P作直线PA平行于y 轴,过点P′作直线P′A平行于x轴,PA与P′A相交于点A,则△PAP′ 的面积为?????? .
?
三、简答题
19、如图,一次函数y=kx+b(k,b为常数,k≠0)的图象与x轴、y轴分别交于A,B两点,且与反比例函数y=(n为常数,且n≠0)的图象在第二象限交于点C,CD⊥x轴,垂足为D,若OB=2OA=3OD=12.
(1)求一次函数与反比例函数的解析式;
(2)记两函数图象的另一个交点为E,求△CDE的面积;
(3)直接写出不等式kx+b≤的解集.
20、如图,在平面直角坐标系中,反比例函数y=(x>0)的图象上有一点A(m,4),过点A作AB⊥x轴于点B,将点B向右平移2个单位长度得到点C,过点C作y轴的平行线交反比例函数的图象于点D.
(1)点D的横坐标为 ?? (用户含m的代数式表示).
(2)当CD=时,求反比例函数所对应的函数表达式.
21、如图,一次函数与反比例函数的图像有公共点A(1,2)。直线轴于点N(3,0),与一次函数和反比例函数的图像分别交于点B、C.
求: (1)一次函数与反比例函数的表达式; (2)△ABC的面积.
22、如图,一次函数y=k1x+b与反比例函数y=的图象交于A(2,m),B(n,﹣2)两点.过点B作BC⊥x轴,垂足为C,且S△ABC=5.
(1)求一次函数与反比例函数的解析式;
(2)根据所给条件,请直接写出不等式k1x+b>的解集;
(3)若P(p,y1),Q(﹣2,y2)是函数y=图象上的两点,且y1≥y2,求实数p的取值范围.
23、如图,在直角坐标系中,Rt△ABC的直角边AC在x轴上,∠ACB=90°,AC=1,反比例函数y=(k>0)的图象经过BC边的中点D(3,1).
(1)求这个反比例函数的表达式;
(2)若△ABC与△EFG成中心对称,且△EFG的边FG在y轴的正半轴上,点E在这个函数的图象上.
①求OF的长;
②连接AF,BE,证明四边形ABEF是正方形.
24、已知反比例函数的图像和一次函数的图像都经过点P(m,2).
(1)求点P的坐标;
(2)求这个一次函数的表达式.
参考答案
一、选择题
1、B;2、D;3、D.;4、A;5、C;6、D;7、D;8、A;9、D;10、C;11、A;12、A;
二、填空题
13、14、y2>y1>y3?? ??
15、20
16、E(2,2) , D? , ??
17、3
18、2? ;???????
三、简答题
19、解:(1)y=-.
(2)140.
(3)由图象可得-4≤x<0或x≥10.
20、【解答】解:(1)∵A(m,4),AB⊥x轴于点B,
∴B的坐标为(m,0),
∵将点B向右平移2个单位长度得到点C,
∴点C的坐标为:(m+2,0),
∵CD∥y轴,
∴点D的横坐标为:m+2;
故答案为:m+2;
(2)∵CD∥y轴,CD=,
∴点D的坐标为:(m+2,),
∵A,D在反比例函数y=(x>0)的图象上,
∴4m=(m+2),
解得:m=1,
∴点A的坐标为(1,4),
∴k=4m=4,
∴反比例函数的解析式为:y=.
21、(1)将A(1,2)代入一次函数解析式得:k+1=2,即k=1,∴一次函数解析式为y=x+1。
将A(1,2)代入反比例解析式得:m=2,
∴反比例解析式为
(2)设一次函数与x轴交于D点,过点A作AE垂直于x轴于点E,
在y=x+1中,令y=0,求出x=﹣1,即OD=1。
∴A(1,2)。∴AE=2,OE=1。
∵N(3,0),∴到B横坐标为3。
将x=3代入一次函数得:y=4,
22、【解答】解:(1)把A(2,m),B(n,﹣2)代入y=得:k2=2m=﹣2n,
即m=﹣n,
则A(2,﹣n),
过A作AE⊥x轴于E,过B作BF⊥y轴于F,延长AE、BF交于D,
∵A(2,﹣n),B(n,﹣2),
∴BD=2﹣n,AD=﹣n+2,BC=|﹣2|=2,
∵S△ABC=?BC?BD
∴×2×(2﹣n)=5,解得:n=﹣3,
即A(2,3),B(﹣3,﹣2),
把A(2,3)代入y=得:k2=6,
即反比例函数的解析式是y=;
把A(2,3),B(﹣3,﹣2)代入y=k1x+b得:,
解得:k1=1,b=1,
即一次函数的解析式是y=x+1;
(2)∵A(2,3),B(﹣3,﹣2),
∴不等式k1x+b>的解集是﹣3<x<0或x>2;
(3)分为两种情况:当点P在第三象限时,要使y1≥y2,实数p的取值范围是P≤﹣2,
当点P在第一象限时,要使y1≥y2,实数p的取值范围是P>0,
即P的取值范围是p≤﹣2或p>0.
23、【解答】解:
(1)∵反比例函数y=(k>0)的图象经过点D(3,1),
∴k=3×1=3,
∴反比例函数表达式为y=;
(2)①∵D为BC的中点,
∴BC=2,
∵△ABC与△EFG成中心对称,
∴△ABC≌△EFG,
∴GF=BC=2,GE=AC=1,
∵点E在反比例函数的图象上,
∴E(1,3),即OG=3,
∴OF=OG﹣GF=1;
②如图,连接AF、BE,
∵AC=1,OC=3,
∴OA=GF=2,
在△AOF和△FGE中
∴△AOF≌△FGE(SAS),
∴∠GFE=∠FAO=∠ABC,
∴∠GFE+∠AFO=∠FAO+∠BAC=90°,
∴EF∥AB,且EF=AB,
∴四边形ABEF为平行四边形,
∴AF=EF,
∴四边形ABEF为菱形,
∵AF⊥EF,
∴四边形ABEF为正方形.
24、(1)P(6,2);(2)
1、选择题
1、下列函数,①y=2x,②y=x,③y=x-1,④y=是反比例函数的个数有(? )
A.0个??? B.1个??? C.2个??? D.3个
2、反比例函数y=的图象位于(? )
A.第一、二象限??? B.第一、三象限??? C.第二、三象限??? D.第二、四象限
3、关于反比例函数y=的图象,下列说法正确的是( )
A.必经过点(1,1) B.两个分支分布在第二、四象限
C.两个分支关于x轴成轴对称 D.两个分支关于原点成中心对称
4、已知矩形的面积为10,则它的长y与宽x之间的关系用图象表示大致为(? )
5、如图,过反比例函数y=(x>0)的图象上一点A作AB⊥x轴于点B,连接AO,若S△AOB=2,则k的值为( )
A.2???? B.3????? C.4???? D.5
6、.如图,A,B两点在反比例函数y=的图象上,C,D两点在反比例函数y=的图象上,AC⊥y轴于点E,BD⊥y轴于点F,AC=2,BD=1,EF=3,则k1-k2的值是( ??)
A.6? B.4? C.3 ? D.2
7、如图,在平面直角坐标系中,?OABC的顶点A的坐标为(-4,0),顶点B在第二象限,∠BAO=60°,BC交y轴于点D,DB∶DC=3∶1.若函数y=(k>0,x>0)的图象经过点C,则k的值为( ?)
A.? B.? C. ? D.
8、如图,点A在双曲线y=上,点B在双曲线y=(k≠0)上,AB∥x轴,分别过点A,B向x轴作垂线,垂足分别为D,C,若矩形ABCD的面积是8,则k的值为( ?)
A.12? B.10? C.8? D.6
9、如图,正比例函数y1=k1x的图象与反比例函数y2=的图象相交于A,B两点,其中点A的横坐标为2,当y1>y2时,x的取值范围是( ?)
A.x<-2或x>2? B.x<-2或0<x<2
C.-2<x<0或0<x<-2? D.-2<x<0或x>2
10、一次函数y=ax+a(a为常数,a≠0)与反比例函数y=(a为常数,a≠0)在同一平面直角坐标系内的图象大致为( ?)
11、如图,△ABC的三个顶点分别为A(1,2),B(2,5),C(6,1).若函数y=在第一象限内的图象与△ABC有交点,则k的取值范围是( )
A.2≤k≤??? B.6≤k≤10 C.2≤k≤6? D.2≤k≤
12、如图,已知A、B是反比例函数y=(k>0,x>0)图象上的两点,BC∥y轴,交x轴于点C.动点P从坐标原点O出发,沿O→A→B→C匀速运动,终点为C.过点P作PQ⊥x轴于Q.设△OPQ的面积为S,点P运动的时间为t,则S关于t的函数图象大致为( )
A.? B.? C.?? D.
二、填空题
13、若反比例函数的图象上有两点A(1,y1),B(2,y2),则y1??????y2(填“>”或“=”或“<”)??
14、反比例函数图象上有三个点,,,其中,则,,的大小关系是????? 。
15、如图,反比例函数的图像上有一点A,且轴,,则k=??? ?.
16、如图,已知四边形AOBE和四边形CBFD均为正方形,反比例函数的图象经过D、E两点,则点E的坐标是 ?;点D的坐标是 ?;△DOE的面积为??? 。
17、如图,为反比例函数的图象在第二象限上的任一点,轴于轴于则矩形的面积??????? ??.
18、如图,设点P是函数在第一象限图象上的任意一点,点P关于原点O的对称点为P′,过点P作直线PA平行于y 轴,过点P′作直线P′A平行于x轴,PA与P′A相交于点A,则△PAP′ 的面积为?????? .
?
三、简答题
19、如图,一次函数y=kx+b(k,b为常数,k≠0)的图象与x轴、y轴分别交于A,B两点,且与反比例函数y=(n为常数,且n≠0)的图象在第二象限交于点C,CD⊥x轴,垂足为D,若OB=2OA=3OD=12.
(1)求一次函数与反比例函数的解析式;
(2)记两函数图象的另一个交点为E,求△CDE的面积;
(3)直接写出不等式kx+b≤的解集.
20、如图,在平面直角坐标系中,反比例函数y=(x>0)的图象上有一点A(m,4),过点A作AB⊥x轴于点B,将点B向右平移2个单位长度得到点C,过点C作y轴的平行线交反比例函数的图象于点D.
(1)点D的横坐标为 ?? (用户含m的代数式表示).
(2)当CD=时,求反比例函数所对应的函数表达式.
21、如图,一次函数与反比例函数的图像有公共点A(1,2)。直线轴于点N(3,0),与一次函数和反比例函数的图像分别交于点B、C.
求: (1)一次函数与反比例函数的表达式; (2)△ABC的面积.
22、如图,一次函数y=k1x+b与反比例函数y=的图象交于A(2,m),B(n,﹣2)两点.过点B作BC⊥x轴,垂足为C,且S△ABC=5.
(1)求一次函数与反比例函数的解析式;
(2)根据所给条件,请直接写出不等式k1x+b>的解集;
(3)若P(p,y1),Q(﹣2,y2)是函数y=图象上的两点,且y1≥y2,求实数p的取值范围.
23、如图,在直角坐标系中,Rt△ABC的直角边AC在x轴上,∠ACB=90°,AC=1,反比例函数y=(k>0)的图象经过BC边的中点D(3,1).
(1)求这个反比例函数的表达式;
(2)若△ABC与△EFG成中心对称,且△EFG的边FG在y轴的正半轴上,点E在这个函数的图象上.
①求OF的长;
②连接AF,BE,证明四边形ABEF是正方形.
24、已知反比例函数的图像和一次函数的图像都经过点P(m,2).
(1)求点P的坐标;
(2)求这个一次函数的表达式.
参考答案
一、选择题
1、B;2、D;3、D.;4、A;5、C;6、D;7、D;8、A;9、D;10、C;11、A;12、A;
二、填空题
13、14、y2>y1>y3?? ??
15、20
16、E(2,2) , D? , ??
17、3
18、2? ;???????
三、简答题
19、解:(1)y=-.
(2)140.
(3)由图象可得-4≤x<0或x≥10.
20、【解答】解:(1)∵A(m,4),AB⊥x轴于点B,
∴B的坐标为(m,0),
∵将点B向右平移2个单位长度得到点C,
∴点C的坐标为:(m+2,0),
∵CD∥y轴,
∴点D的横坐标为:m+2;
故答案为:m+2;
(2)∵CD∥y轴,CD=,
∴点D的坐标为:(m+2,),
∵A,D在反比例函数y=(x>0)的图象上,
∴4m=(m+2),
解得:m=1,
∴点A的坐标为(1,4),
∴k=4m=4,
∴反比例函数的解析式为:y=.
21、(1)将A(1,2)代入一次函数解析式得:k+1=2,即k=1,∴一次函数解析式为y=x+1。
将A(1,2)代入反比例解析式得:m=2,
∴反比例解析式为
(2)设一次函数与x轴交于D点,过点A作AE垂直于x轴于点E,
在y=x+1中,令y=0,求出x=﹣1,即OD=1。
∴A(1,2)。∴AE=2,OE=1。
∵N(3,0),∴到B横坐标为3。
将x=3代入一次函数得:y=4,
22、【解答】解:(1)把A(2,m),B(n,﹣2)代入y=得:k2=2m=﹣2n,
即m=﹣n,
则A(2,﹣n),
过A作AE⊥x轴于E,过B作BF⊥y轴于F,延长AE、BF交于D,
∵A(2,﹣n),B(n,﹣2),
∴BD=2﹣n,AD=﹣n+2,BC=|﹣2|=2,
∵S△ABC=?BC?BD
∴×2×(2﹣n)=5,解得:n=﹣3,
即A(2,3),B(﹣3,﹣2),
把A(2,3)代入y=得:k2=6,
即反比例函数的解析式是y=;
把A(2,3),B(﹣3,﹣2)代入y=k1x+b得:,
解得:k1=1,b=1,
即一次函数的解析式是y=x+1;
(2)∵A(2,3),B(﹣3,﹣2),
∴不等式k1x+b>的解集是﹣3<x<0或x>2;
(3)分为两种情况:当点P在第三象限时,要使y1≥y2,实数p的取值范围是P≤﹣2,
当点P在第一象限时,要使y1≥y2,实数p的取值范围是P>0,
即P的取值范围是p≤﹣2或p>0.
23、【解答】解:
(1)∵反比例函数y=(k>0)的图象经过点D(3,1),
∴k=3×1=3,
∴反比例函数表达式为y=;
(2)①∵D为BC的中点,
∴BC=2,
∵△ABC与△EFG成中心对称,
∴△ABC≌△EFG,
∴GF=BC=2,GE=AC=1,
∵点E在反比例函数的图象上,
∴E(1,3),即OG=3,
∴OF=OG﹣GF=1;
②如图,连接AF、BE,
∵AC=1,OC=3,
∴OA=GF=2,
在△AOF和△FGE中
∴△AOF≌△FGE(SAS),
∴∠GFE=∠FAO=∠ABC,
∴∠GFE+∠AFO=∠FAO+∠BAC=90°,
∴EF∥AB,且EF=AB,
∴四边形ABEF为平行四边形,
∴AF=EF,
∴四边形ABEF为菱形,
∵AF⊥EF,
∴四边形ABEF为正方形.
24、(1)P(6,2);(2)
