六年级下册数学课件小升初行程问题——追及问题(共18张PPT)北师大版
文档属性
| 名称 | 六年级下册数学课件小升初行程问题——追及问题(共18张PPT)北师大版 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-02 00:00:00 | ||
图片预览



文档简介
(共18张PPT)
追及问题
一、情景引入
警察追小偷,警察发现前面的小偷在偷东西,大喊:“站住!别跑”,小偷看到警察后立马撒腿就跑。与此同时,警察也跑去追小偷。警察每分钟跑110米,小偷每分钟跑80米,经过5分钟警察追上小偷,问:警察发现小偷时距离多少米?
站住! 别跑
不跑的是傻子
警察比小偷多跑的路程
追及路程
二、合作探索
追及路程=速度差×追及时间
甲
乙
=V甲×T追及
=V乙×T追及
S甲
S乙
S追及
=S甲—S乙
=V甲×T追及—V乙×T追及
=(V甲—V乙)×T追及
=V差×T追及
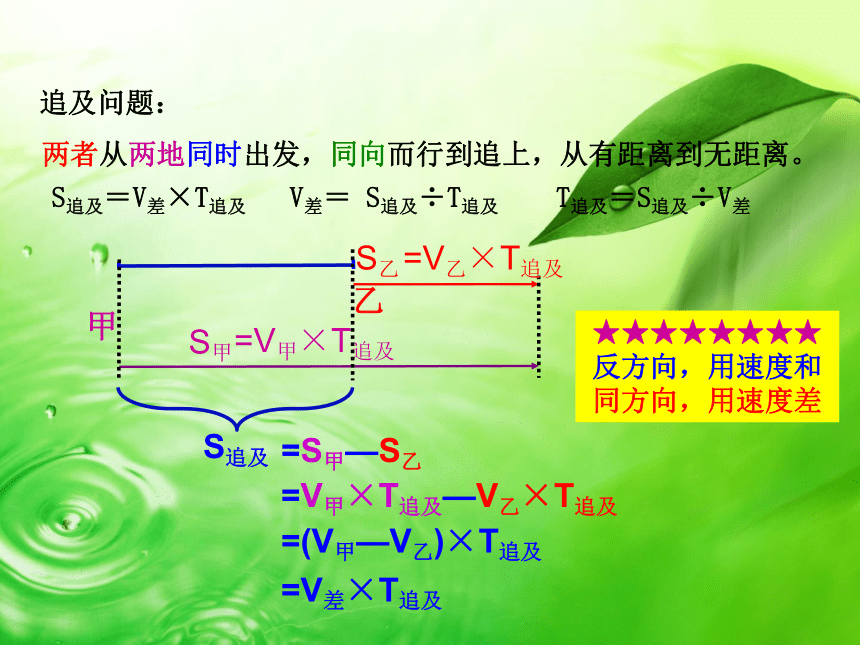
S追及=V差×T追及 V差= S追及÷T追及 T追及=S追及÷V差
追及问题:
两者从两地同时出发,同向而行到追上,从有距离到无距离。
★★★★★★★★
反方向,用速度和
同方向,用速度差
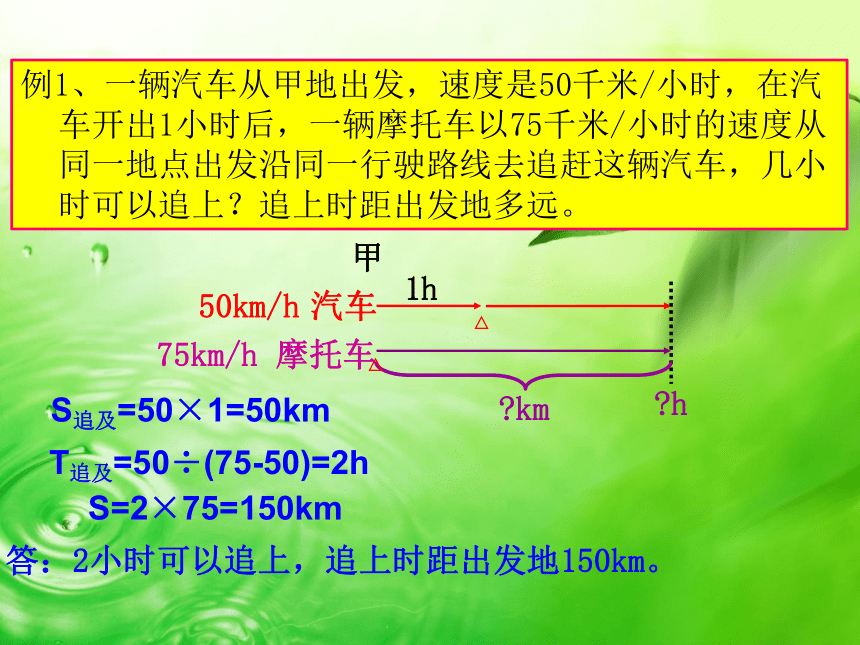
例1、一辆汽车从甲地出发,速度是50千米/小时,在汽车开出1小时后,一辆摩托车以75千米/小时的速度从同一地点出发沿同一行驶路线去追赶这辆汽车,几小时可以追上?追上时距出发地多远。
甲
汽车
50km/h
1h
摩托车
75km/h
?h
?km
△
△
S追及=50×1=50km
T追及=50÷(75-50)=2h
S=2×75=150km
答:2小时可以追上,追上时距出发地150km。
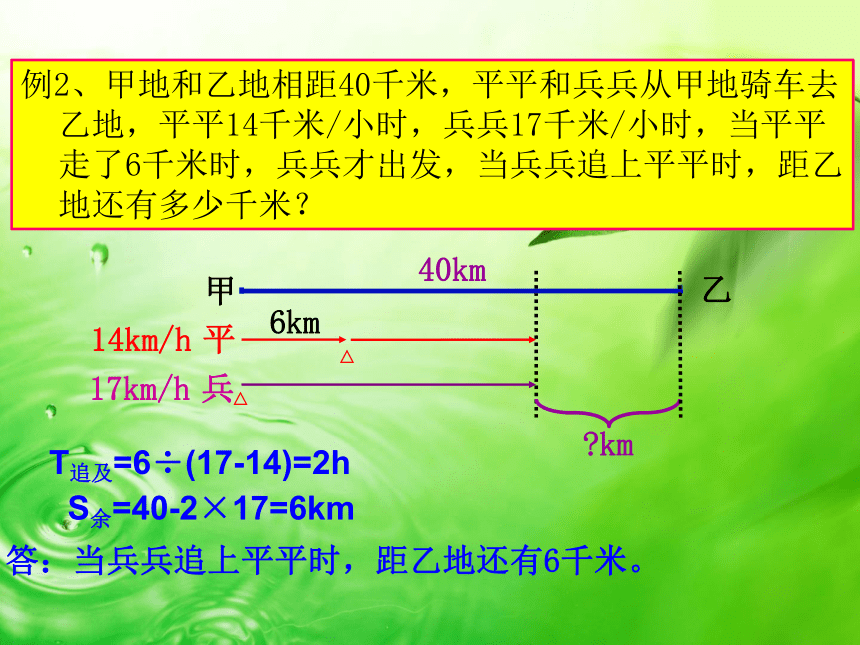
例2、甲地和乙地相距40千米,平平和兵兵从甲地骑车去乙地,平平14千米/小时,兵兵17千米/小时,当平平走了6千米时,兵兵才出发,当兵兵追上平平时,距乙地还有多少千米?
甲
平
14km/h
6km
兵
17km/h
?km
△
△
T追及=6÷(17-14)=2h
S余=40-2×17=6km
答:当兵兵追上平平时,距乙地还有6千米。
乙
40km
例4、玲玲从学校出发步行去电影院看电影,速度为60米/分钟,走了10分钟后,李老师从学校骑自行车去追玲玲,结果在距学校900米的地方遇到玲玲,李老师每分钟行多少米?
学校
玲玲
60m/分
10分钟
老师
?m/分
900m
△
△
T玲玲=900÷60=15(分)
T追及=15-10=5(分)
答:李老师每分钟行180米。
电影院
5分钟
5分钟
V老师=900÷5=180(米/分)
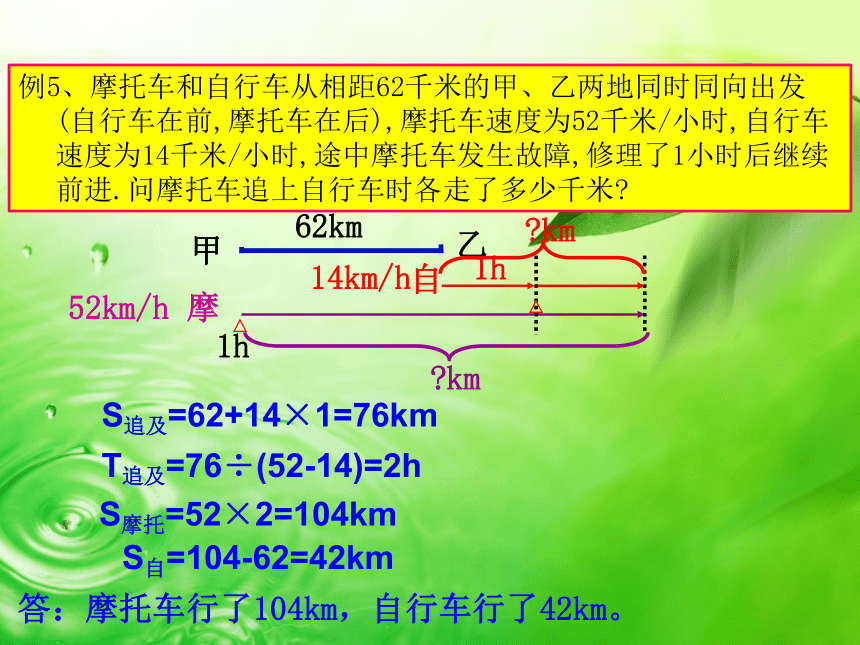
例5、摩托车和自行车从相距62千米的甲、乙两地同时同向出发(自行车在前,摩托车在后),摩托车速度为52千米/小时,自行车速度为14千米/小时,途中摩托车发生故障,修理了1小时后继续前进.问摩托车追上自行车时各走了多少千米?
甲
自
14km/h
1h
摩
52km/h
?km
△
△
S追及=62+14×1=76km
T追及=76÷(52-14)=2h
答:摩托车行了104km,自行车行了42km。
乙
S摩托=52×2=104km
62km
1h
?km
S自=104-62=42km
例3、甲、乙两人沿运动场的跑道跑步,甲每分钟跑300米,乙每分钟跑280米,跑道一圈长400米。如果两人同时由同地向同方向起跑,那么甲经过多少分钟才能第一次追上乙?
★★★★★★★★
在环形行程问题中:
两者同时同地同向而行,当快者第一次追上慢者时,S差=1圈,当快着第N次追上慢者时,S差=N圈。
两者同时同地背向而行,第一次相遇时,S和=1圈,第N次相遇时,S和=N圈。
400÷(300-280)=20(分)
答:甲经过20分钟才能第一次追上乙。
例5、家离图书馆4.8km,弟弟从家出发以60m/分速度步行去图书馆。15分钟后,哥哥骑自行车从家出发去追赶弟弟,自行车的速度是240m/分。问: (1) 哥哥在离家多远处追上弟弟?(2) 哥哥追上弟弟后不久到达图书馆,又马上折回,过不久与弟弟相遇,那么相遇处离图书馆多少km?
4.8千米
弟60米/分
S追及=60×15=900m
△
△
哥240米/分
家
图书馆
T追及=900÷(240—60)=5(分)
S哥=5×240=1200(米)
S相遇=2×(4.8×1000—1200)=7200(米)
T相遇=7200÷(60+240)=24(分)
S=4.8×1000-(15+5+24)×60=2160(米)
多次相遇问题:
两者从两地同时出发,相向而行并往返行驶:
第1次相遇时S和=1个全程,第n次相遇时S和=(2n-1)个全程;
第1次相遇:S和=1个全程
第2次相遇:S和=3个全程
第3次相遇:S和=5个全程
A
B
甲
乙
一遇
二遇
两者从两地同时出发,相向而行并往返行驶:
当S和=奇数个全程时,相遇次数=(奇数+1)÷2; 当S和=偶数个全程时,相遇次数=偶数÷2。
当S和=1个全程时,第1次相遇
当S和=2个全程时,相遇1次并错过
当S和=3个全程时,第2次相遇
当S和=4个全程时,相遇2次并错过
两者从同一地点同时出发同向而行,并往返行驶:
第1次相遇时S和=2个全程;第N次相遇时S和=2N个全程;
A
B
甲
乙
1遇
2遇
第1次相遇:S和=2个全程
第2次相遇:S和=4个全程
第N次相遇:S和=2N个全程
第1次追上:S差=2个全程
第2次追上:S差=4个全程
第N次追上:S差=2N个全程
两者从同一地点同时出发同向而行,并往返行驶:
当快者第1次追上慢者时S差=2个全程;
当快者第N次追上慢者时S差=2N个全程;
1追
例1、两辆汽车同时从南北两站同时出发,相对开出,
(一)、第一次在离南站100千米的地方相遇,之后两车继续以
原来的速度前进,各自到 达对方出发站后立即返回,又在
①离南站20千米处相遇; ②离北站20千米处相遇;
③离中点南侧30千米处相遇; ④离中点北侧30千米处相遇;
⑤二次相遇点在中点南侧,且与中点的距离相当于南北两站间距离的10%;
⑥二次相遇点在中点北侧,且与中点的距离相当于南北两站间距离的30%;
⑦二次相遇点与南站的距离相当于南北两站间距离的20%;
⑧二次相遇点与北站的距离相当于南北两站间距离的20%;
八种不同情况下南北两站之间的距离是多少千米?
(100×3+20)÷2=160m
100×3—20=280m
(100×3—30)÷1.5=180m
(100×3+30)÷1.5=220m
100×3÷(2-20%)=500/3 m
100×3÷(1+20%)=250m
100×3÷(1.5+10%)=187.5 m
100×3÷(1.5-30%)=250 m
二、第一次在中点南侧100米处相遇,之后两车继续以原来的速度
前进,各自到达对方出发站后立即返回,
又在①离南站800米处相遇;
②离北站300米处相遇;
③二次相遇点与南站的距离相当于南北两站间距离的80%;
④二次相遇点与北站的距离相当于南北两站间距离的30%;
⑤二次相遇点与中点的距离相当于南北两站间距离的30%;
求以上五种不同情况下南北两站之间的距离是多少千米?
( 800—100×3)×2=1000m
(100×3+300)×2=1200m
100×3÷(80%—0.5)=1000m
100×3÷(0.5—30%)=1500m
100×3÷30%=1000m
☆例2.两辆汽车同时从南北两站相对开出,第一次在离南站55km的
地方相遇,之后两车继续以原来的速度前进。各自到站后都
立即返回,又在距离南站15km处相遇。两站相距多少km?
南
北
①
②
15km
55km
一遇
二遇
分析:
第一次相遇时
S①+S②=1个全程,
其中S①=55km
第二次相遇时
S①+S②=3个全程,
其中S①=55×3=165km
=2个全程-15km
解:(55×3+15)÷2=90km
答:两站相距90km。
☆例3. 甲、乙、丙三人在一条公路上同时出发,甲从A地到B地,速 度为60m/min,乙、丙从B地到A地,乙的速度为50m/min,丙 的速度为45m/min,甲乙相遇后2min,与丙相遇。求A、B两 地之间的距离。
甲:
乙
丙
60m
50m
45m
甲、丙2min的S相遇(60+45) ×2
甲、乙相遇时,
乙、丙的S差
(60+45)×2
A
B
÷(50-45)
×(60+50)=4620m
答:A、B两地之间的距离为4620米。
多人相遇2种类型:S=V后和×T÷V同差×V先和
例4、A、B两地相距1800米。甲乙两人同时从A、B两地出发,若相向而行,12分钟相遇;若同向而行,90分钟甲追上乙。甲从A地出发走到B地要用几分钟?
V和=1800÷12=150(米/分)
V差=1800÷90=20(米/分)
V甲=(150+20)÷2=85(米/分)
例5、甲、乙两人在一条长90米的路上来回跑步,甲的速度是每秒3米,乙的速度是每秒2米,如果它们分别从直路的两端出发,12分钟时,他们共相遇几次?
两者从两地同时出发,相向而行并往返行驶:
当S和=奇数个全程时,相遇次数=(奇数+1)÷2; 当S和=偶数个全程时,相遇次数=偶数÷2。
S和=(3+2)×12×60=3600(米)
3600÷90=40(个)
相遇次数=40÷2=20(次)
答:他们共相遇20次。
☆例6、甲、乙两人同时从A地出发,在直道A、B两地往返跑步,甲每分钟72米,乙每分钟48米,甲乙第二次迎面相遇与甲第二次从后面追上乙的两地相距80米,求A、B两地相距多少米?
两者从同一地点同时出发同向而行,并往返行驶:
第1次相遇时S和=2个全程;第N次相遇时S和=2N个全程;
两者从同一地点同时出发同向而行,并往返行驶:
当快者第1次追上慢者时S差=2个全程;
当快者第N次追上慢者时S差=2N个全程;
二遇:S和=4个全程
二遇时的S甲=4÷(72+48)×72=2.4
二追:S差=4个全程
二追时的S甲=4÷(72-48)×72=12
S=80÷0.4=200(米)
答:A、B两地相距200米
追及问题
一、情景引入
警察追小偷,警察发现前面的小偷在偷东西,大喊:“站住!别跑”,小偷看到警察后立马撒腿就跑。与此同时,警察也跑去追小偷。警察每分钟跑110米,小偷每分钟跑80米,经过5分钟警察追上小偷,问:警察发现小偷时距离多少米?
站住! 别跑
不跑的是傻子
警察比小偷多跑的路程
追及路程
二、合作探索
追及路程=速度差×追及时间
甲
乙
=V甲×T追及
=V乙×T追及
S甲
S乙
S追及
=S甲—S乙
=V甲×T追及—V乙×T追及
=(V甲—V乙)×T追及
=V差×T追及
S追及=V差×T追及 V差= S追及÷T追及 T追及=S追及÷V差
追及问题:
两者从两地同时出发,同向而行到追上,从有距离到无距离。
★★★★★★★★
反方向,用速度和
同方向,用速度差
例1、一辆汽车从甲地出发,速度是50千米/小时,在汽车开出1小时后,一辆摩托车以75千米/小时的速度从同一地点出发沿同一行驶路线去追赶这辆汽车,几小时可以追上?追上时距出发地多远。
甲
汽车
50km/h
1h
摩托车
75km/h
?h
?km
△
△
S追及=50×1=50km
T追及=50÷(75-50)=2h
S=2×75=150km
答:2小时可以追上,追上时距出发地150km。
例2、甲地和乙地相距40千米,平平和兵兵从甲地骑车去乙地,平平14千米/小时,兵兵17千米/小时,当平平走了6千米时,兵兵才出发,当兵兵追上平平时,距乙地还有多少千米?
甲
平
14km/h
6km
兵
17km/h
?km
△
△
T追及=6÷(17-14)=2h
S余=40-2×17=6km
答:当兵兵追上平平时,距乙地还有6千米。
乙
40km
例4、玲玲从学校出发步行去电影院看电影,速度为60米/分钟,走了10分钟后,李老师从学校骑自行车去追玲玲,结果在距学校900米的地方遇到玲玲,李老师每分钟行多少米?
学校
玲玲
60m/分
10分钟
老师
?m/分
900m
△
△
T玲玲=900÷60=15(分)
T追及=15-10=5(分)
答:李老师每分钟行180米。
电影院
5分钟
5分钟
V老师=900÷5=180(米/分)
例5、摩托车和自行车从相距62千米的甲、乙两地同时同向出发(自行车在前,摩托车在后),摩托车速度为52千米/小时,自行车速度为14千米/小时,途中摩托车发生故障,修理了1小时后继续前进.问摩托车追上自行车时各走了多少千米?
甲
自
14km/h
1h
摩
52km/h
?km
△
△
S追及=62+14×1=76km
T追及=76÷(52-14)=2h
答:摩托车行了104km,自行车行了42km。
乙
S摩托=52×2=104km
62km
1h
?km
S自=104-62=42km
例3、甲、乙两人沿运动场的跑道跑步,甲每分钟跑300米,乙每分钟跑280米,跑道一圈长400米。如果两人同时由同地向同方向起跑,那么甲经过多少分钟才能第一次追上乙?
★★★★★★★★
在环形行程问题中:
两者同时同地同向而行,当快者第一次追上慢者时,S差=1圈,当快着第N次追上慢者时,S差=N圈。
两者同时同地背向而行,第一次相遇时,S和=1圈,第N次相遇时,S和=N圈。
400÷(300-280)=20(分)
答:甲经过20分钟才能第一次追上乙。
例5、家离图书馆4.8km,弟弟从家出发以60m/分速度步行去图书馆。15分钟后,哥哥骑自行车从家出发去追赶弟弟,自行车的速度是240m/分。问: (1) 哥哥在离家多远处追上弟弟?(2) 哥哥追上弟弟后不久到达图书馆,又马上折回,过不久与弟弟相遇,那么相遇处离图书馆多少km?
4.8千米
弟60米/分
S追及=60×15=900m
△
△
哥240米/分
家
图书馆
T追及=900÷(240—60)=5(分)
S哥=5×240=1200(米)
S相遇=2×(4.8×1000—1200)=7200(米)
T相遇=7200÷(60+240)=24(分)
S=4.8×1000-(15+5+24)×60=2160(米)
多次相遇问题:
两者从两地同时出发,相向而行并往返行驶:
第1次相遇时S和=1个全程,第n次相遇时S和=(2n-1)个全程;
第1次相遇:S和=1个全程
第2次相遇:S和=3个全程
第3次相遇:S和=5个全程
A
B
甲
乙
一遇
二遇
两者从两地同时出发,相向而行并往返行驶:
当S和=奇数个全程时,相遇次数=(奇数+1)÷2; 当S和=偶数个全程时,相遇次数=偶数÷2。
当S和=1个全程时,第1次相遇
当S和=2个全程时,相遇1次并错过
当S和=3个全程时,第2次相遇
当S和=4个全程时,相遇2次并错过
两者从同一地点同时出发同向而行,并往返行驶:
第1次相遇时S和=2个全程;第N次相遇时S和=2N个全程;
A
B
甲
乙
1遇
2遇
第1次相遇:S和=2个全程
第2次相遇:S和=4个全程
第N次相遇:S和=2N个全程
第1次追上:S差=2个全程
第2次追上:S差=4个全程
第N次追上:S差=2N个全程
两者从同一地点同时出发同向而行,并往返行驶:
当快者第1次追上慢者时S差=2个全程;
当快者第N次追上慢者时S差=2N个全程;
1追
例1、两辆汽车同时从南北两站同时出发,相对开出,
(一)、第一次在离南站100千米的地方相遇,之后两车继续以
原来的速度前进,各自到 达对方出发站后立即返回,又在
①离南站20千米处相遇; ②离北站20千米处相遇;
③离中点南侧30千米处相遇; ④离中点北侧30千米处相遇;
⑤二次相遇点在中点南侧,且与中点的距离相当于南北两站间距离的10%;
⑥二次相遇点在中点北侧,且与中点的距离相当于南北两站间距离的30%;
⑦二次相遇点与南站的距离相当于南北两站间距离的20%;
⑧二次相遇点与北站的距离相当于南北两站间距离的20%;
八种不同情况下南北两站之间的距离是多少千米?
(100×3+20)÷2=160m
100×3—20=280m
(100×3—30)÷1.5=180m
(100×3+30)÷1.5=220m
100×3÷(2-20%)=500/3 m
100×3÷(1+20%)=250m
100×3÷(1.5+10%)=187.5 m
100×3÷(1.5-30%)=250 m
二、第一次在中点南侧100米处相遇,之后两车继续以原来的速度
前进,各自到达对方出发站后立即返回,
又在①离南站800米处相遇;
②离北站300米处相遇;
③二次相遇点与南站的距离相当于南北两站间距离的80%;
④二次相遇点与北站的距离相当于南北两站间距离的30%;
⑤二次相遇点与中点的距离相当于南北两站间距离的30%;
求以上五种不同情况下南北两站之间的距离是多少千米?
( 800—100×3)×2=1000m
(100×3+300)×2=1200m
100×3÷(80%—0.5)=1000m
100×3÷(0.5—30%)=1500m
100×3÷30%=1000m
☆例2.两辆汽车同时从南北两站相对开出,第一次在离南站55km的
地方相遇,之后两车继续以原来的速度前进。各自到站后都
立即返回,又在距离南站15km处相遇。两站相距多少km?
南
北
①
②
15km
55km
一遇
二遇
分析:
第一次相遇时
S①+S②=1个全程,
其中S①=55km
第二次相遇时
S①+S②=3个全程,
其中S①=55×3=165km
=2个全程-15km
解:(55×3+15)÷2=90km
答:两站相距90km。
☆例3. 甲、乙、丙三人在一条公路上同时出发,甲从A地到B地,速 度为60m/min,乙、丙从B地到A地,乙的速度为50m/min,丙 的速度为45m/min,甲乙相遇后2min,与丙相遇。求A、B两 地之间的距离。
甲:
乙
丙
60m
50m
45m
甲、丙2min的S相遇(60+45) ×2
甲、乙相遇时,
乙、丙的S差
(60+45)×2
A
B
÷(50-45)
×(60+50)=4620m
答:A、B两地之间的距离为4620米。
多人相遇2种类型:S=V后和×T÷V同差×V先和
例4、A、B两地相距1800米。甲乙两人同时从A、B两地出发,若相向而行,12分钟相遇;若同向而行,90分钟甲追上乙。甲从A地出发走到B地要用几分钟?
V和=1800÷12=150(米/分)
V差=1800÷90=20(米/分)
V甲=(150+20)÷2=85(米/分)
例5、甲、乙两人在一条长90米的路上来回跑步,甲的速度是每秒3米,乙的速度是每秒2米,如果它们分别从直路的两端出发,12分钟时,他们共相遇几次?
两者从两地同时出发,相向而行并往返行驶:
当S和=奇数个全程时,相遇次数=(奇数+1)÷2; 当S和=偶数个全程时,相遇次数=偶数÷2。
S和=(3+2)×12×60=3600(米)
3600÷90=40(个)
相遇次数=40÷2=20(次)
答:他们共相遇20次。
☆例6、甲、乙两人同时从A地出发,在直道A、B两地往返跑步,甲每分钟72米,乙每分钟48米,甲乙第二次迎面相遇与甲第二次从后面追上乙的两地相距80米,求A、B两地相距多少米?
两者从同一地点同时出发同向而行,并往返行驶:
第1次相遇时S和=2个全程;第N次相遇时S和=2N个全程;
两者从同一地点同时出发同向而行,并往返行驶:
当快者第1次追上慢者时S差=2个全程;
当快者第N次追上慢者时S差=2N个全程;
二遇:S和=4个全程
二遇时的S甲=4÷(72+48)×72=2.4
二追:S差=4个全程
二追时的S甲=4÷(72-48)×72=12
S=80÷0.4=200(米)
答:A、B两地相距200米
