沪科版九年级数学下册24.1.2 中心对称与中心对称图形 课件(共28张PPT)
文档属性
| 名称 | 沪科版九年级数学下册24.1.2 中心对称与中心对称图形 课件(共28张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-03 00:00:00 | ||
图片预览




文档简介
(共28张PPT)
第2课时 中心对称
与中心对称图形
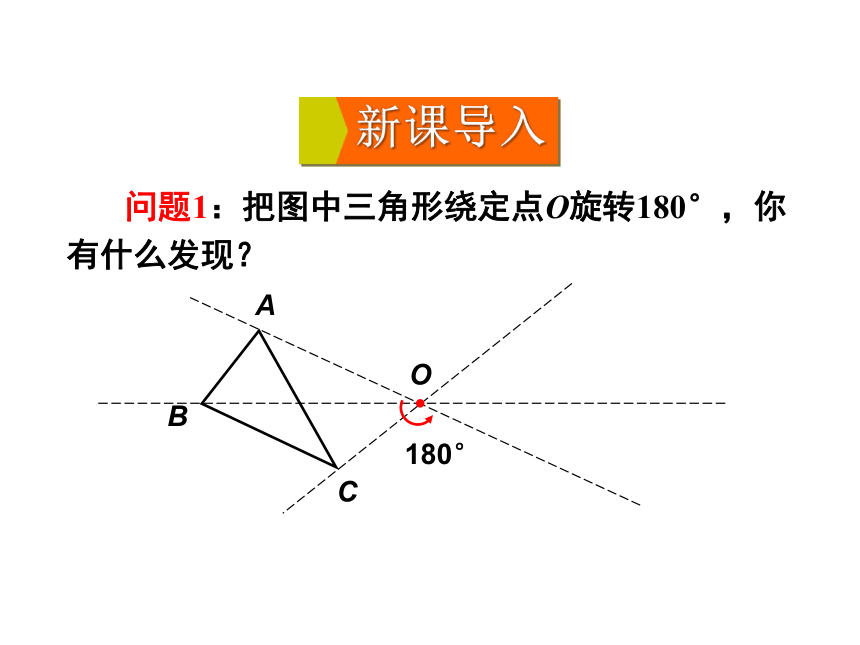
问题1:把图中三角形绕定点O旋转180°,你有什么发现?
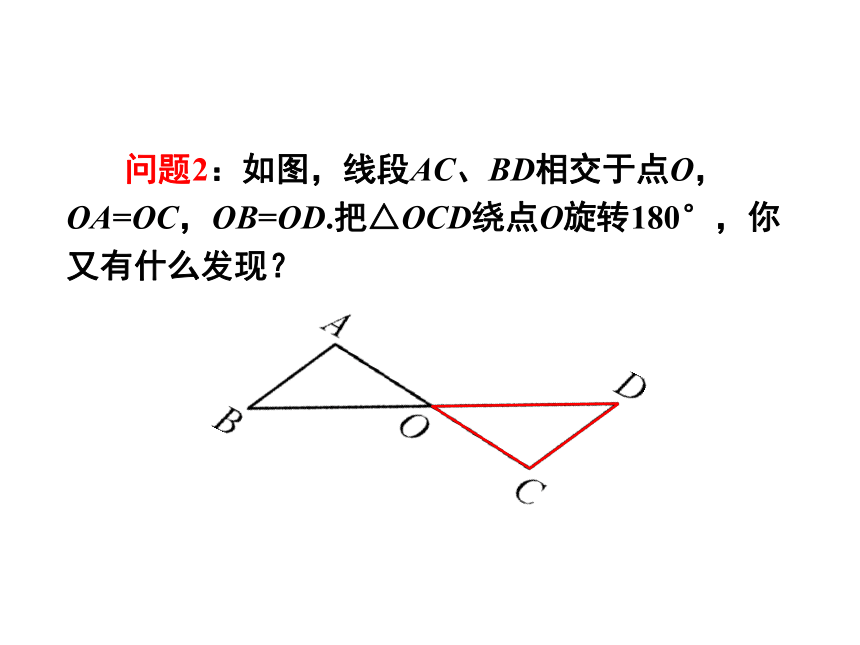
问题2:如图,线段AC、BD相交于点O,OA=OC,OB=OD.把△OCD绕点O旋转180°,你又有什么发现?
你发现了什么?
把一个图形 ,如果它 ,那么就说这两个图形关于这个点 或 ,这个点叫做 . 这两个图形在旋转后能重合的对应点叫做关于对称中心的对称点.
绕着某一点旋转180°
能够与另一个图形重合
对称
中心对称
对称中心(简称中心)
A′
B′
C′
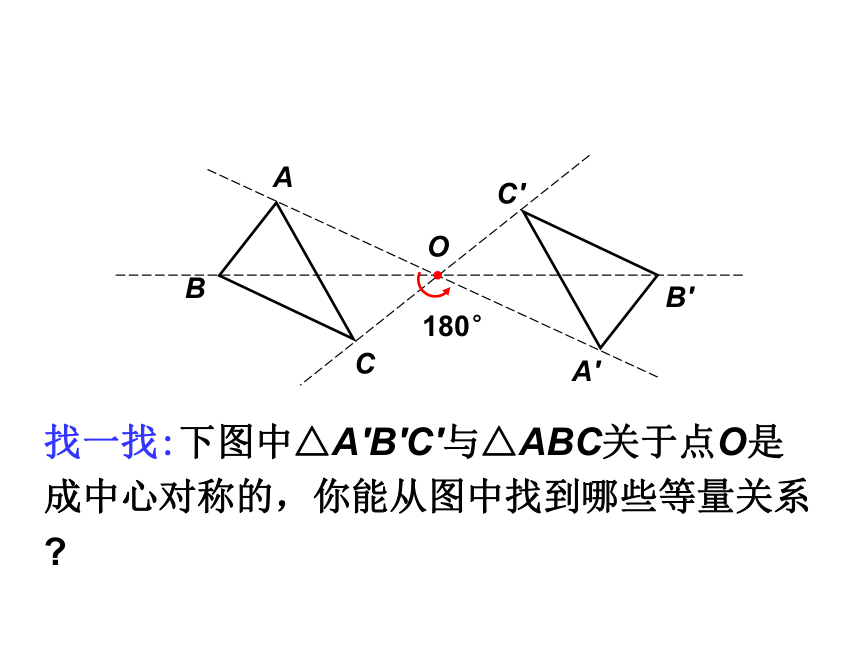
找一找:下图中△A′B′C′与△ABC关于点O是成中心对称的,你能从图中找到哪些等量关系?
思考:观察上图,两个图形形成中心对称,说一说中心对称有什么特性?
1.关于中心对称的两个图形,对称点所连线段都经过对称中心,并且被对称中心所平分.
2.关于中心对称的两个图形是全等形.
归纳:中心对称的性质
想一想:中心对称与轴对称有什么区别?又有什么联系?
轴对称 中心对称
有一条对称轴---直线 有一个对称中心—点
图形沿对称轴对折(翻折180°)后重合 图形绕对称中心旋转180°后重合
对称点的连线被对称轴垂直平分 对称点连线经过对称中心,且被对称中心平分
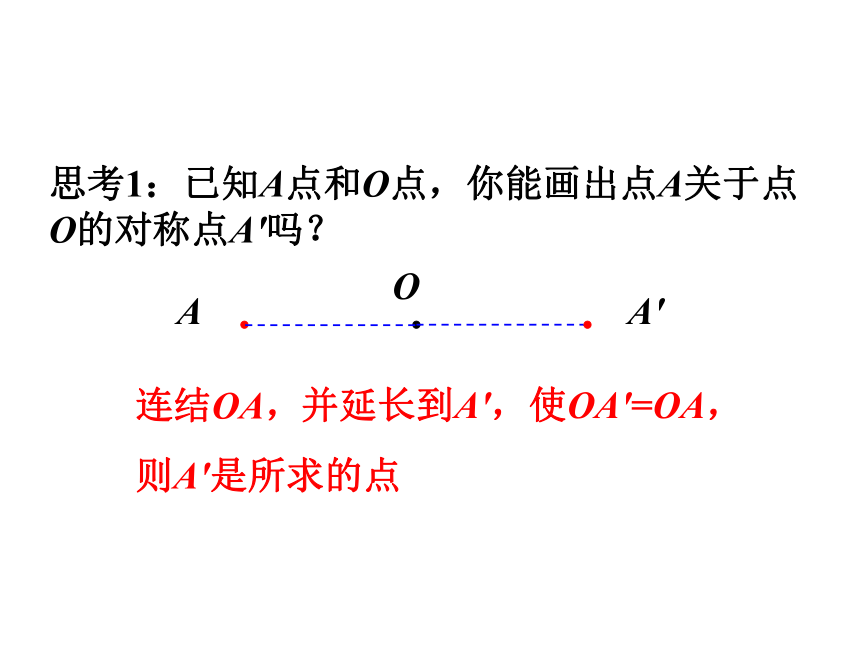
思考1:已知A点和O点,你能画出点A关于点O的对称点A'吗?
A
O
A'
连结OA,
并延长到A',使OA'=OA,
则A'是所求的点
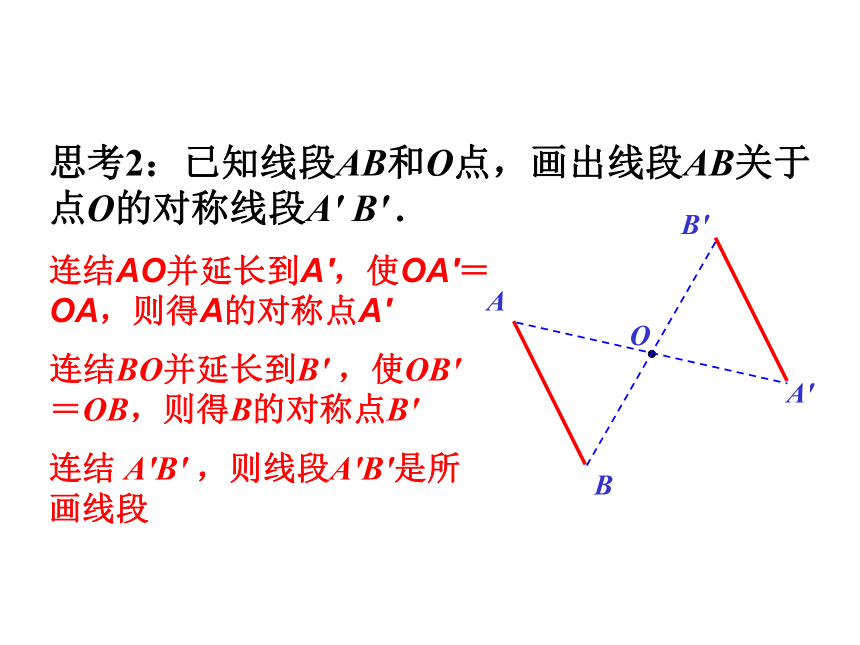
思考2:已知线段AB和O点,画出线段AB关于点O的对称线段A' B' .
O
A
B
连结AO并延长到A',使OA'=OA,则得A的对称点A'
A'
连结BO并延长到B' ,使OB' =OB,则得B的对称点B'
B'
连结 A'B' ,则线段A'B'是所画线段
例 如图,已知四边形ABCD和点O,试画出四边形ABCD关于点O成中心对称的图形A'B'C'D'.
怎么办?
分析:要画出四边形ABCD关于点O成中心对称的图形,只要画出A,B,C,D四点关于点O的对应点,再顺次连接各对应点即可.
1.连结AO并延长到A',使OA'=OA,得到点A的对应点A'
A′
2.同理,可作出点B,C,D的对应点B',C',D'.
B′
C′
D′
3.顺次连接点A',B',C',D'.则四边形A'B'C'D'即为所作.
想一想:如图,已知△ABC与△A′B′C′中心对称,怎样求出它们的对称中心O?
观察:将下面的图形绕O点旋转180°,你有什么发现?
A
B
O
B
A
C
D
如果一个图形绕一个点旋转180°后,能和原来的图形互相重合,那么这个图形叫做中心对称图形;这个点叫做它的对称中心;互相重合的点叫做对称点.
下面哪些图形是中心对称图形?
问题:我们平时见过的几何图形中,有哪些是中心对称图形?并指出对称中心.
比较中心对称和中心对称图形的概念,试说明它们有何区别与联系.
区别:中心对称是针对两个图形而言的,而中心对称图形是针对单个图形而言的.
联系:如果把成中心对称的两个图形看成一个整体,则该图形为中心对称图形;如果把一个中心对称图形相互对称的两部分看成两个图形,则它们成中心对称.
中心对称图形
1.下列图形中既是轴对称图形又是中心对称图形的是( )
A.角 B.等边三角形 C.线段 D.平行四边形
2.下列多边形中,是中心对称图形而不是轴对称图形的是( )
A.平行四边形 B.矩形 C.菱形 D.正方形
C
A
3.下列标志中,可以看做是中心对称图形的是( )
D
4. 如图,△ABC与△A1B1C1关于点O成中心对称,下列说法:①∠BAC=∠B1A1C1;②AC=A1C1; ③OA=OA1;④△ABC与△A1B1C1的面积相等.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
D
o
5. 如图,在△ABC中,AB=AC,若将△ABC绕点C顺时针旋转180°得到△FEC.
(1)试猜想AE与BF有何关系?说明理由;
(2)若△ABC的面积为3cm2,求四边形ABFE的面积.
解:(1)AE∥BF,AE=BF;
理由:∵△ABC绕点C顺时针旋转180°得到△FEC,
∴△ABC≌△FEC,
∴AB=FE,∠ABC=∠FEC,
∴AB∥FE,
∴四边形ABFE为平行四边形,AE∥BF,AE=BF .
(2)S四边形ABFE=4S△ABC=12 cm2.
中心对称是针对两个图形而言的,中心对称图形是针对一个图形而言的.
把一个图形绕着某一个点旋转180°后,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形.
1.从课后习题中选取;
2.完成练习册本课时的习题。
第2课时 中心对称
与中心对称图形
问题1:把图中三角形绕定点O旋转180°,你有什么发现?
问题2:如图,线段AC、BD相交于点O,OA=OC,OB=OD.把△OCD绕点O旋转180°,你又有什么发现?
你发现了什么?
把一个图形 ,如果它 ,那么就说这两个图形关于这个点 或 ,这个点叫做 . 这两个图形在旋转后能重合的对应点叫做关于对称中心的对称点.
绕着某一点旋转180°
能够与另一个图形重合
对称
中心对称
对称中心(简称中心)
A′
B′
C′
找一找:下图中△A′B′C′与△ABC关于点O是成中心对称的,你能从图中找到哪些等量关系?
思考:观察上图,两个图形形成中心对称,说一说中心对称有什么特性?
1.关于中心对称的两个图形,对称点所连线段都经过对称中心,并且被对称中心所平分.
2.关于中心对称的两个图形是全等形.
归纳:中心对称的性质
想一想:中心对称与轴对称有什么区别?又有什么联系?
轴对称 中心对称
有一条对称轴---直线 有一个对称中心—点
图形沿对称轴对折(翻折180°)后重合 图形绕对称中心旋转180°后重合
对称点的连线被对称轴垂直平分 对称点连线经过对称中心,且被对称中心平分
思考1:已知A点和O点,你能画出点A关于点O的对称点A'吗?
A
O
A'
连结OA,
并延长到A',使OA'=OA,
则A'是所求的点
思考2:已知线段AB和O点,画出线段AB关于点O的对称线段A' B' .
O
A
B
连结AO并延长到A',使OA'=OA,则得A的对称点A'
A'
连结BO并延长到B' ,使OB' =OB,则得B的对称点B'
B'
连结 A'B' ,则线段A'B'是所画线段
例 如图,已知四边形ABCD和点O,试画出四边形ABCD关于点O成中心对称的图形A'B'C'D'.
怎么办?
分析:要画出四边形ABCD关于点O成中心对称的图形,只要画出A,B,C,D四点关于点O的对应点,再顺次连接各对应点即可.
1.连结AO并延长到A',使OA'=OA,得到点A的对应点A'
A′
2.同理,可作出点B,C,D的对应点B',C',D'.
B′
C′
D′
3.顺次连接点A',B',C',D'.则四边形A'B'C'D'即为所作.
想一想:如图,已知△ABC与△A′B′C′中心对称,怎样求出它们的对称中心O?
观察:将下面的图形绕O点旋转180°,你有什么发现?
A
B
O
B
A
C
D
如果一个图形绕一个点旋转180°后,能和原来的图形互相重合,那么这个图形叫做中心对称图形;这个点叫做它的对称中心;互相重合的点叫做对称点.
下面哪些图形是中心对称图形?
问题:我们平时见过的几何图形中,有哪些是中心对称图形?并指出对称中心.
比较中心对称和中心对称图形的概念,试说明它们有何区别与联系.
区别:中心对称是针对两个图形而言的,而中心对称图形是针对单个图形而言的.
联系:如果把成中心对称的两个图形看成一个整体,则该图形为中心对称图形;如果把一个中心对称图形相互对称的两部分看成两个图形,则它们成中心对称.
中心对称图形
1.下列图形中既是轴对称图形又是中心对称图形的是( )
A.角 B.等边三角形 C.线段 D.平行四边形
2.下列多边形中,是中心对称图形而不是轴对称图形的是( )
A.平行四边形 B.矩形 C.菱形 D.正方形
C
A
3.下列标志中,可以看做是中心对称图形的是( )
D
4. 如图,△ABC与△A1B1C1关于点O成中心对称,下列说法:①∠BAC=∠B1A1C1;②AC=A1C1; ③OA=OA1;④△ABC与△A1B1C1的面积相等.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
D
o
5. 如图,在△ABC中,AB=AC,若将△ABC绕点C顺时针旋转180°得到△FEC.
(1)试猜想AE与BF有何关系?说明理由;
(2)若△ABC的面积为3cm2,求四边形ABFE的面积.
解:(1)AE∥BF,AE=BF;
理由:∵△ABC绕点C顺时针旋转180°得到△FEC,
∴△ABC≌△FEC,
∴AB=FE,∠ABC=∠FEC,
∴AB∥FE,
∴四边形ABFE为平行四边形,AE∥BF,AE=BF .
(2)S四边形ABFE=4S△ABC=12 cm2.
中心对称是针对两个图形而言的,中心对称图形是针对一个图形而言的.
把一个图形绕着某一个点旋转180°后,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形.
1.从课后习题中选取;
2.完成练习册本课时的习题。
