人教版七年级下册 第五章 相交线与平行线 5.2 平行线及其判定 同步练习(含答案)
文档属性
| 名称 | 人教版七年级下册 第五章 相交线与平行线 5.2 平行线及其判定 同步练习(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 88.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-02 00:00:00 | ||
图片预览


文档简介
平行线及其判定 同步练习
一.选择题(共12小题)
1.下列命题,其中为真命题的是( )
①经过直线外一点,有且只有一条直线与已知直线平行;
②同位角相等;
③过一点有且只有一条直线与已知直线垂直;
④对顶角相等.
A.①② B.①③④ C.①④ D.②③④
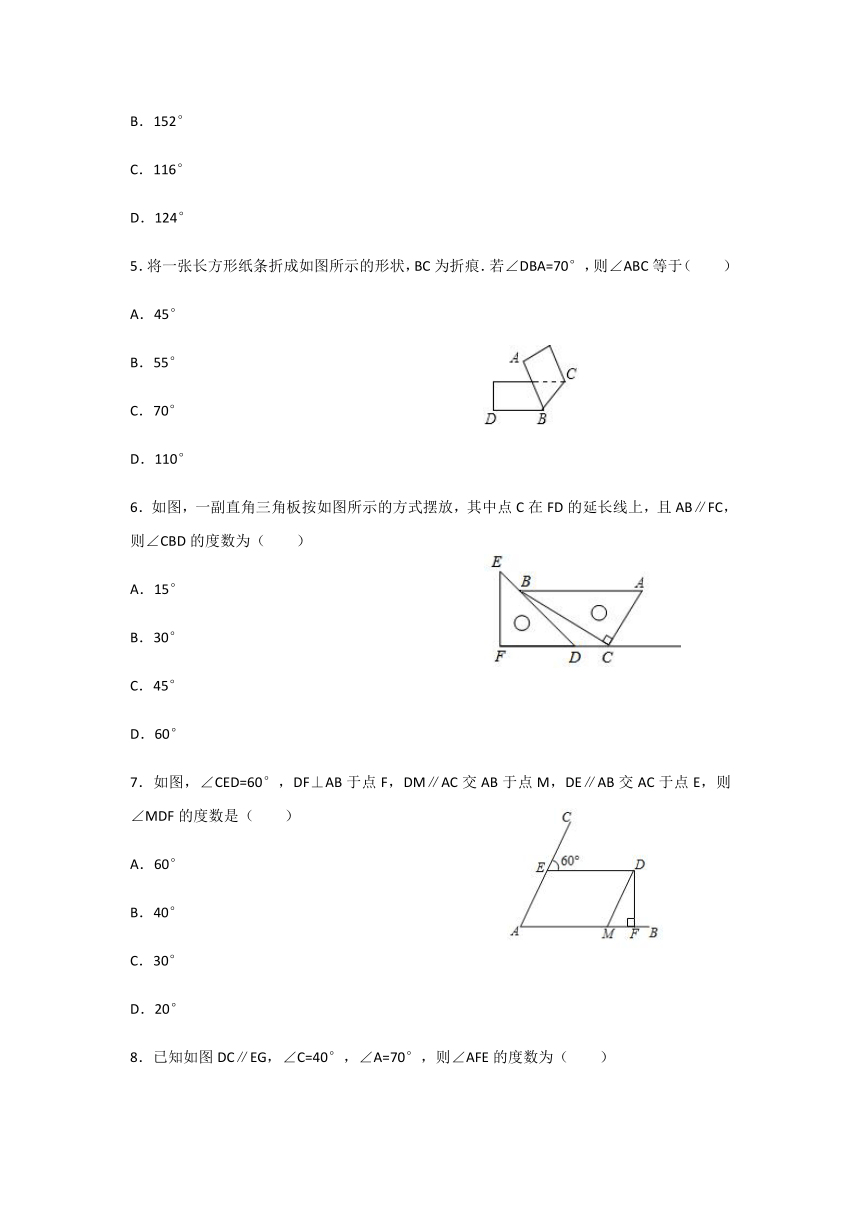
2.如图,已知AB∥CD,直线AB,CD被BC所截,E点在BC上,若∠1=45°,∠2=35°,则∠3=( )
A.65°
B.70°
C.75°
D.80°
3.如图,直线a,b被直线m所截,若a∥b,∠2=62°,则∠1=( )
A.62°
B.108°
C.118°
D.128°
4.如图,AB∥CD,∠1=56°,FG平分∠EFD,则∠FGB的度数等于( )
A.122°
B.152°
C.116°
D.124°
5.将一张长方形纸条折成如图所示的形状,BC为折痕.若∠DBA=70°,则∠ABC等于( )
A.45°
B.55°
C.70°
D.110°
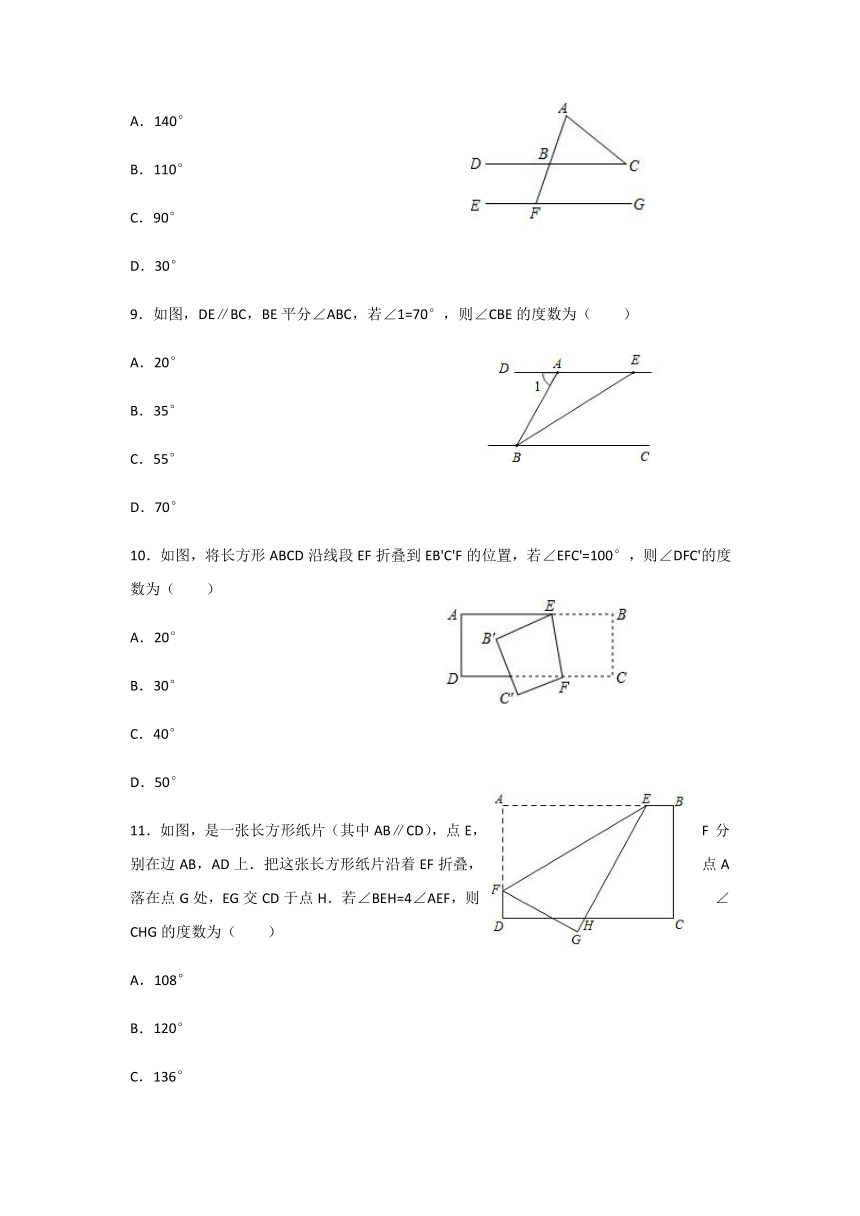
6.如图,一副直角三角板按如图所示的方式摆放,其中点C在FD的延长线上,且AB∥FC,则∠CBD的度数为( )
A.15°
B.30°
C.45°
D.60°
7.如图,∠CED=60°,DF⊥AB于点F,DM∥AC交AB于点M,DE∥AB交AC于点E,则∠MDF的度数是( )
A.60°
B.40°
C.30°
D.20°
8.已知如图DC∥EG,∠C=40°,∠A=70°,则∠AFE的度数为( )
A.140°
B.110°
C.90°
D.30°
9.如图,DE∥BC,BE平分∠ABC,若∠1=70°,则∠CBE的度数为( )
A.20°
B.35°
C.55°
D.70°
10.如图,将长方形ABCD沿线段EF折叠到EB'C'F的位置,若∠EFC'=100°,则∠DFC'的度数为( )
A.20°
B.30°
C.40°
D.50°
11.如图,是一张长方形纸片(其中AB∥CD),点E,F分别在边AB,AD上.把这张长方形纸片沿着EF折叠,点A落在点G处,EG交CD于点H.若∠BEH=4∠AEF,则∠CHG的度数为( )
A.108°
B.120°
C.136°
D.144°
12.如图,AB∥CD,EF与AB,CD分别交于点G,H,∠CHG的平分线HM交AB于点M,若∠EGB=50°,则∠GMH的度数为( )
A.50°
B.55°
C.60°
D.65°
二.填空题(共5小题)
13.如图,在△ABC中,CD平分∠ACB,DE∥BC,交AC于点E.若∠AED=50°,则∠D的度数为 .
14.如图,AB∥CD,AC∥BD,∠1=28°,则∠2的度数为
15.如图AB∥CD,CB∥DE,∠B=50°,则∠D=
16.如图,E为△ABC边CA延长线上一点,过点E作ED∥BC.若∠BAC=70°,∠CED=50°,则∠B=
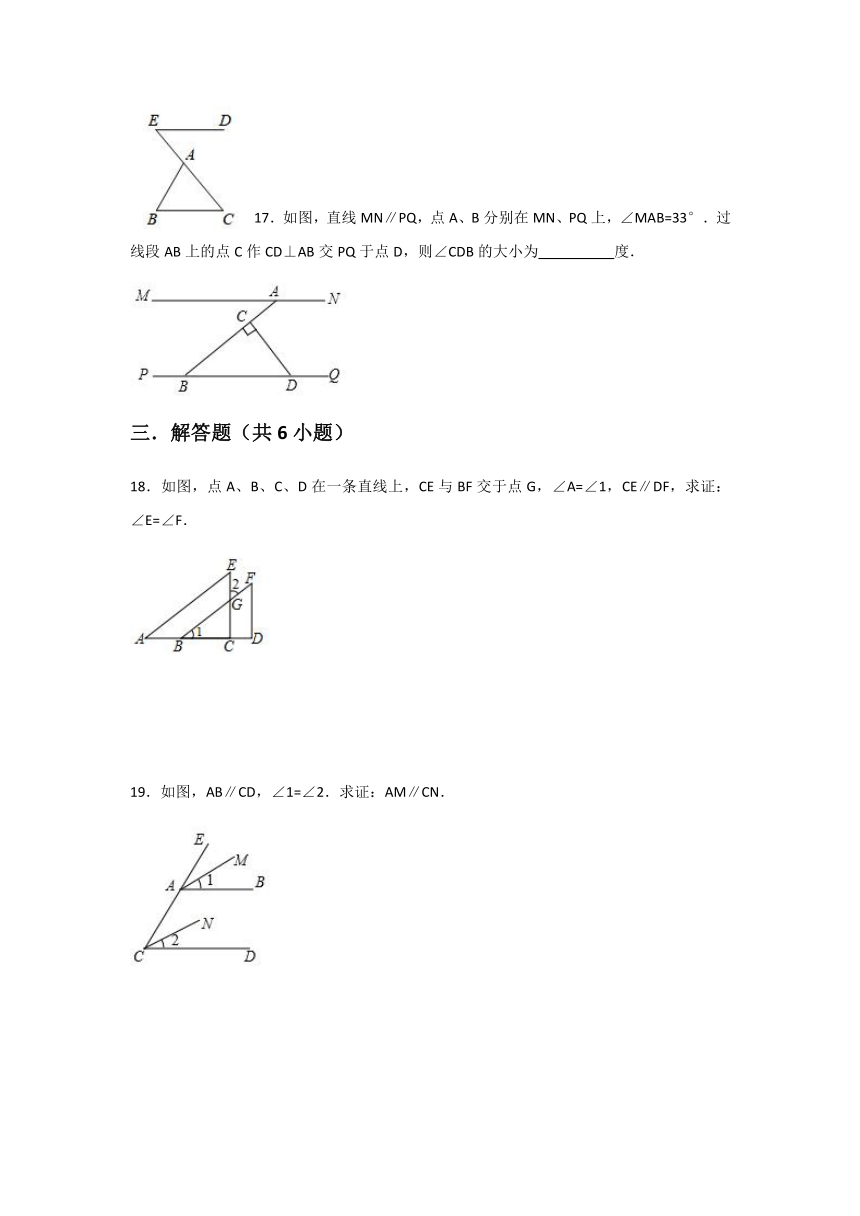
17.如图,直线MN∥PQ,点A、B分别在MN、PQ上,∠MAB=33°.过线段AB上的点C作CD⊥AB交PQ于点D,则∠CDB的大小为 度.
三.解答题(共6小题)
18.如图,点A、B、C、D在一条直线上,CE与BF交于点G,∠A=∠1,CE∥DF,求证:∠E=∠F.
19.如图,AB∥CD,∠1=∠2.求证:AM∥CN.
20.如图,直线AB∥CD,BC平分∠ABD,∠1=54°,求∠2的度数.
21.如图,AB∥CD,△EFG的顶点F,G分别落在直线AB,CD上,GE交AB于点H,GE平分∠FGD.若∠EFG=90°,∠E=35°,求∠EFB的度数.
22.如图,直线EF∥GH,点A在EF上,AC交GH于点B,若∠FAC=72°,∠ACD=58°,点D在GH上,求∠BDC的度数.
23.如图1,E是直线AB,CD内部一点,AB∥CD,连接EA,ED.
(1)探究猜想:
①若∠A=30°,∠D=40°,则∠AED等于多少度?
②若∠A=20°,∠D=60°,则∠AED等于多少度?
③猜想图1中∠AED,∠EAB,∠EDC的关系并证明你的结论.
(2)拓展应用:
如图2,射线FE与矩形ABCD的边AB交于点E,与边CD交于点F,①②③④分别是被射线FE隔开的4个区域(不含边界,其中区域③、④位于直线AB上方,P是位于以上四个区域上的点,猜想:∠PEB,∠PFC,∠EPF的关系(不要求证明).
参考答案
1-5:CDCBB 6-10:ACBBA 11-12:BD
13、25°
14、28°
15、130
16、60
17、57
18、:∵CE∥DF,
∴∠ACE=∠D,
∵∠A=∠1,
∴180°-∠ACE-∠A=180°-∠D-∠1,
又∵∠E=180°-∠ACE-∠A,∠F=180°-∠D-∠1,
∴∠E=∠F.
19、:∵AB∥CD,
∴∠EAB=∠ECD,
∵∠1=∠2,
∴∠EAM=∠ECN,
∴AM∥CN.
20、:∵直线AB∥CD,
∴∠1=∠3
∵∠1=54°,
∴∠3=54°
∵BC平分∠ABD,
∴∠ABD=2∠3=108°,
∵AB∥CD,
∴∠BDC=180°-∠ABD=72°,
∴∠2=∠BDC=72°.
21、:∵∠EFG=90°,∠E=35°,
∴∠FGH=55°,
∵GE平分∠FGD,AB∥CD,
∴∠FHG=∠HGD=∠FGH=55°,
∵∠FHG是△EFH的外角,
∴∠EFB=55°-35°=20
22、:∵EF∥GH,
∴∠ABD+∠FAC=180°,
∴∠ABD=180°-72°=108°,
∵∠ABD=∠ACD+∠BDC,
∴∠BDC=∠ABD-∠ACD=108°-58°=50°.
23、:(1)①∠AED=70°;
②∠AED=80°;
③猜想:∠AED=∠EAB+∠EDC,
证明:延长AE交DC于点F,
∵AB∥DC,
∴∠EAB=∠EFD,
∵∠AED为△EDF的外角,
∴∠AED=∠EDF+∠EFD=∠EAB+∠EDC;
(2)根据题意得:
点P在区域①时,∠EPF=360°-(∠PEB+∠PFC);
点P在区域②时,∠EPF=∠PEB+∠PFC;
点P在区域③时,∠EPF=∠PEB-∠PFC;
点P在区域④时,∠EPF=∠PFC-∠PEB
