2.1平面向量的实际背景及基本概念(共21张PPT)
文档属性
| 名称 | 2.1平面向量的实际背景及基本概念(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 504.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-03 00:00:00 | ||
图片预览






文档简介
(共31张PPT)
平面向量的实际背景
及基本概念
问题:如图,一只老鼠和一只猫相距6米,老鼠以每秒4米的速度逃窜,猫以每秒7米的速度追,猫在多少时间里会追上老鼠?
猫与老鼠
嘻嘻!大笨猫!
唉, 哪儿去了?
方向
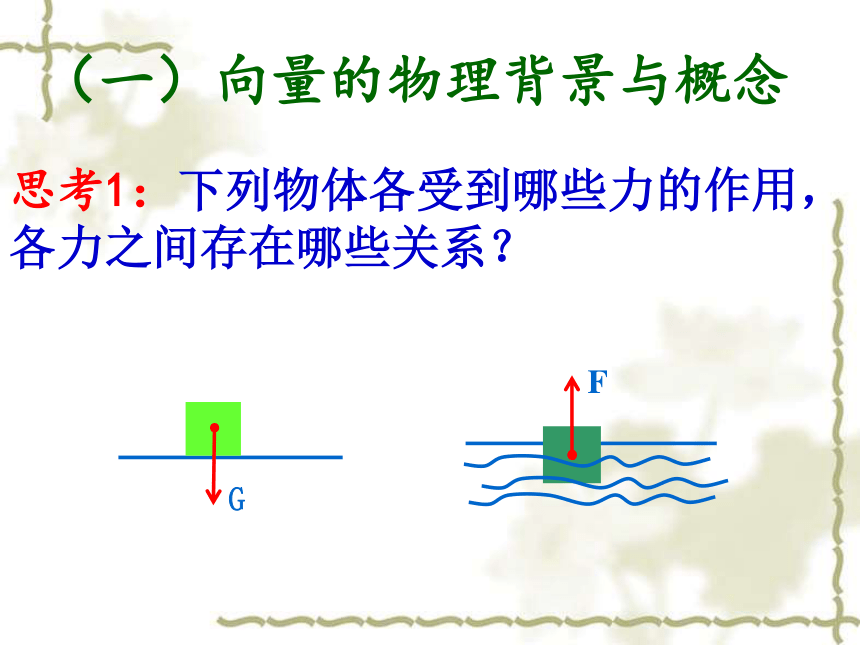
思考1:下列物体各受到哪些力的作用,各力之间存在哪些关系?
(一)向量的物理背景与概念
F
G
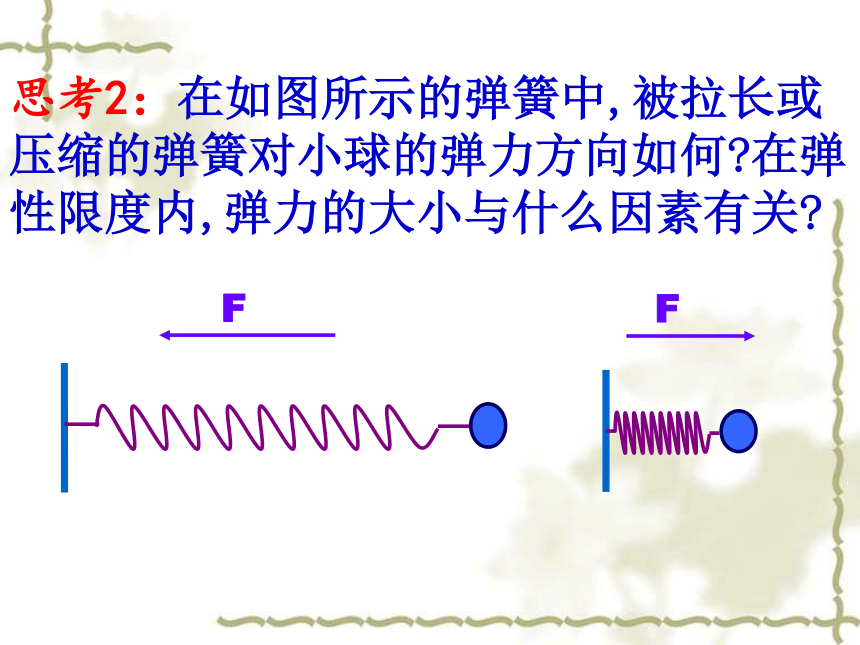
思考2:在如图所示的弹簧中,被拉长或压缩的弹簧对小球的弹力方向如何?在弹性限度内,弹力的大小与什么因素有关?
F
F
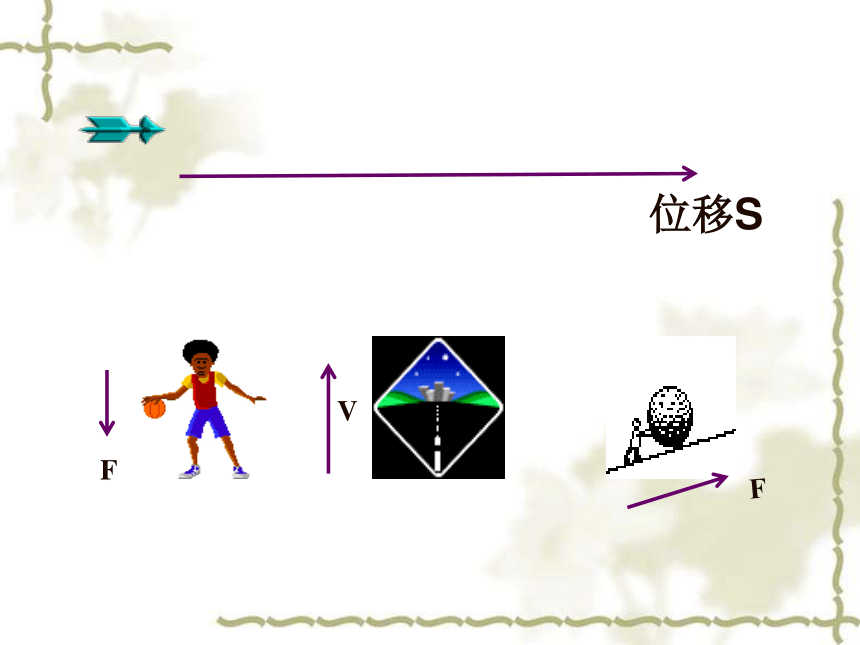
位移S
F
V
F
数学中,把既有大小,又有方向的量叫做向量(vector).
向量的概念:
向量——矢量
数量——标量
思考3:如何用几何方式表示向量?
有向线段:
带有方向的线段叫做有向线段.
.
.
A
B
(起点)
(终点)
向量的字母表示
a,b,c,…
(二)向量的几何表示
起点
方向
长度
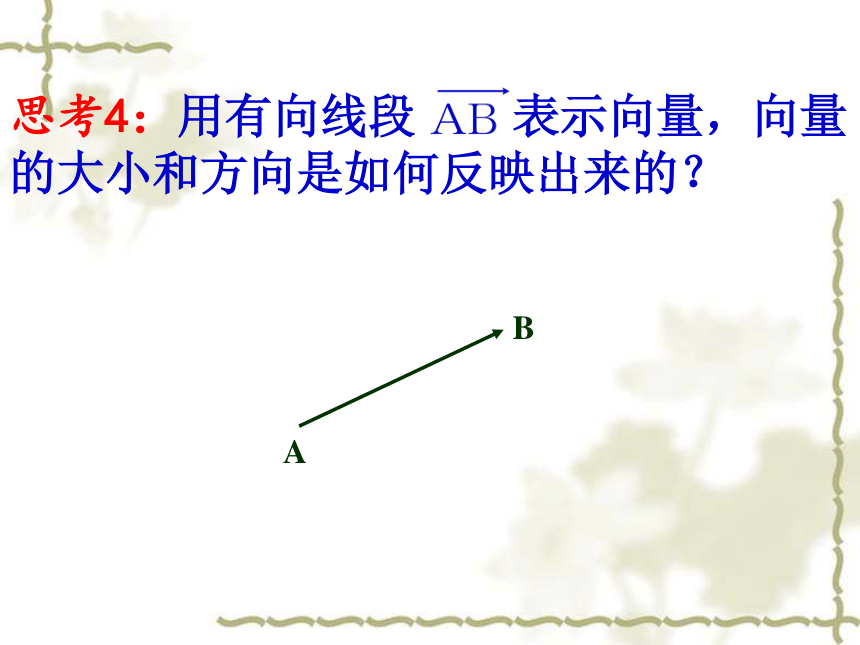
思考4:用有向线段 表示向量,向量的大小和方向是如何反映出来的?
A
B
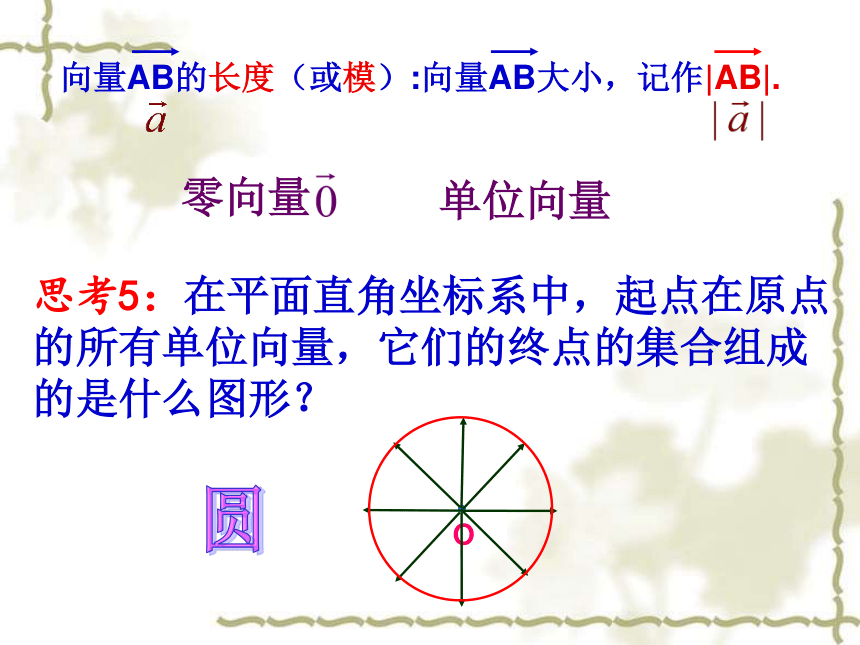
向量AB的长度(或模):向量AB大小,记作|AB|.
零向量
单位向量
思考5:在平面直角坐标系中,起点在原点的所有单位向量,它们的终点的集合组成的是什么图形?
O
圆
相等向量:长度相等且方向相同的向量.
(三)相等向量与平行向量
思考6:两个向量能否比较大小?
规定:0 = 0
B
A
C
D
对于一个向量,只要不改变它的长度和方向,就可以任意平行移动。
规定:零向量与任一向量平行.
思考7:平行向量所在的直线一定互相平行吗?
向量相等 向量平行
平行向量:方向相同或相反的非零向量.
平行向量也叫做共线向量
l
平行向量:
思考8:如果非零向量 是共线向量,那么点A、B、C、D是否一定共线?
B
A
D
C
思考9:用有向线段表示非零向量
,如果 ,那么A、B、C、D四点的位置关系有哪几种可能情形?
A
B
C
D
练 习
练习1.对于向量a、b、c,若a =b,
b =c,那么a = c吗?
变式:对于非零向量a、b、c,若a // b, b // c,那么a // c吗?
练习2.对于向量a、b、c,若a // b, b // c,那么a // c吗?
O
A
B
C
D
E
F
例1. 如图,设O是正六边形ABCDEF的中心,分别写出图中与 相等的向量.
变式一:与向量 长度相等的向量有多少个?
变式二:是否存在与向量 长度相等、方向相反的向量,若存在,共有几个?
变式三:与向量 共线的向量有哪些,共几个?
11
1
3
练习3:如图,EF是△ABC的中位线,AD是BC边的中线,在以A、B、C、D、E、F为端点的有向线段表示的向量中请分别写出
(1)与向量CD共线的向量有___个,
分别是______________________;
(2)与向量DF的模一定相等的向
量有__个,分别是_______________;
(3)与向量DE相等的向量有__个,
分别是___________.
A
B
C
D
E
F
7
5
2
根据下列小题的条件,分别判断四边形ABCD
的形状:
(1) ; (2) 且
(1)四边形ABCD是
平行四边形。
(2)四边形ABCD是菱形。
探究
练习4:一辆汽车从A点出发向西行驶了100公里到达B点,然后又改变方向向西偏北50度走了200公里到达C点,最后又改变方向,向东行驶了100公里到达D点.
(1)做出向量
(2)求
A
B
C
D
向量
定义
长度(模)
表示
几何表示法:有向线段
符号表示法:
零向量
单位向量
向量间
的关系
相等
平行(共线)
a ,b,
AB
向量的有关概念
特殊向量
大小
大小和方向
方向
小 结
作 业
平面向量的实际背景
及基本概念
问题:如图,一只老鼠和一只猫相距6米,老鼠以每秒4米的速度逃窜,猫以每秒7米的速度追,猫在多少时间里会追上老鼠?
猫与老鼠
嘻嘻!大笨猫!
唉, 哪儿去了?
方向
思考1:下列物体各受到哪些力的作用,各力之间存在哪些关系?
(一)向量的物理背景与概念
F
G
思考2:在如图所示的弹簧中,被拉长或压缩的弹簧对小球的弹力方向如何?在弹性限度内,弹力的大小与什么因素有关?
F
F
位移S
F
V
F
数学中,把既有大小,又有方向的量叫做向量(vector).
向量的概念:
向量——矢量
数量——标量
思考3:如何用几何方式表示向量?
有向线段:
带有方向的线段叫做有向线段.
.
.
A
B
(起点)
(终点)
向量的字母表示
a,b,c,…
(二)向量的几何表示
起点
方向
长度
思考4:用有向线段 表示向量,向量的大小和方向是如何反映出来的?
A
B
向量AB的长度(或模):向量AB大小,记作|AB|.
零向量
单位向量
思考5:在平面直角坐标系中,起点在原点的所有单位向量,它们的终点的集合组成的是什么图形?
O
圆
相等向量:长度相等且方向相同的向量.
(三)相等向量与平行向量
思考6:两个向量能否比较大小?
规定:0 = 0
B
A
C
D
对于一个向量,只要不改变它的长度和方向,就可以任意平行移动。
规定:零向量与任一向量平行.
思考7:平行向量所在的直线一定互相平行吗?
向量相等 向量平行
平行向量:方向相同或相反的非零向量.
平行向量也叫做共线向量
l
平行向量:
思考8:如果非零向量 是共线向量,那么点A、B、C、D是否一定共线?
B
A
D
C
思考9:用有向线段表示非零向量
,如果 ,那么A、B、C、D四点的位置关系有哪几种可能情形?
A
B
C
D
练 习
练习1.对于向量a、b、c,若a =b,
b =c,那么a = c吗?
变式:对于非零向量a、b、c,若a // b, b // c,那么a // c吗?
练习2.对于向量a、b、c,若a // b, b // c,那么a // c吗?
O
A
B
C
D
E
F
例1. 如图,设O是正六边形ABCDEF的中心,分别写出图中与 相等的向量.
变式一:与向量 长度相等的向量有多少个?
变式二:是否存在与向量 长度相等、方向相反的向量,若存在,共有几个?
变式三:与向量 共线的向量有哪些,共几个?
11
1
3
练习3:如图,EF是△ABC的中位线,AD是BC边的中线,在以A、B、C、D、E、F为端点的有向线段表示的向量中请分别写出
(1)与向量CD共线的向量有___个,
分别是______________________;
(2)与向量DF的模一定相等的向
量有__个,分别是_______________;
(3)与向量DE相等的向量有__个,
分别是___________.
A
B
C
D
E
F
7
5
2
根据下列小题的条件,分别判断四边形ABCD
的形状:
(1) ; (2) 且
(1)四边形ABCD是
平行四边形。
(2)四边形ABCD是菱形。
探究
练习4:一辆汽车从A点出发向西行驶了100公里到达B点,然后又改变方向向西偏北50度走了200公里到达C点,最后又改变方向,向东行驶了100公里到达D点.
(1)做出向量
(2)求
A
B
C
D
向量
定义
长度(模)
表示
几何表示法:有向线段
符号表示法:
零向量
单位向量
向量间
的关系
相等
平行(共线)
a ,b,
AB
向量的有关概念
特殊向量
大小
大小和方向
方向
小 结
作 业
