2.4.1平面向量的数量积 40张ppt
文档属性
| 名称 | 2.4.1平面向量的数量积 40张ppt |

|
|
| 格式 | zip | ||
| 文件大小 | 829.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-03 00:00:00 | ||
图片预览




文档简介
2.4 平面向量的数量积
2.4.1 平面向量数量积的物理
背景及其含义
向量的夹角
O A
B
?
已知两个非零向量 和 ,作 , ,则
叫做向量 和 的夹角.
OA a? OB b? ???AOB
)1800(
?? ??? a
ba
b
a
b
,a b记作
复习
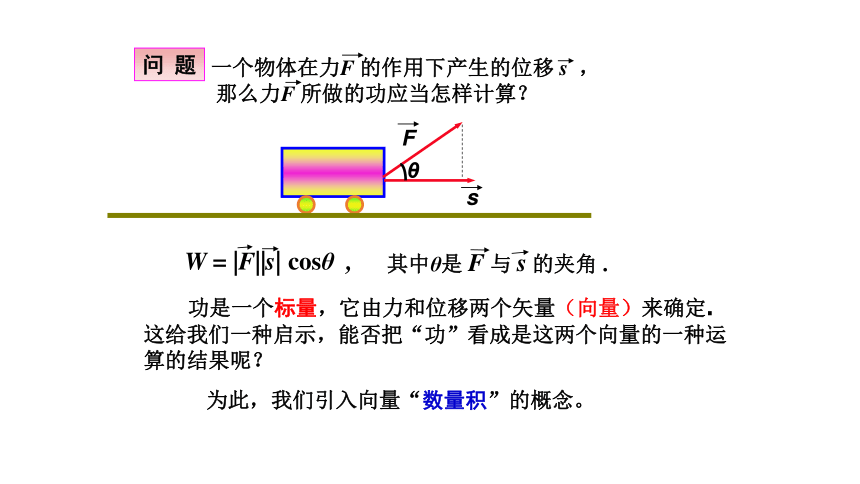
问 题
θ
s
F
一个物体在力F 的作用下产生的位移 s ,
那么力F 所做的功应当怎样计算?
为此,我们引入向量“数量积”的概念。
功是一个标量,它由力和位移两个矢量(向量)来确定.
这给我们一种启示,能否把“功”看成是这两个向量的一种运
算的结果呢?
其中θ是 F 与 s 的夹角 .W = |F||s| cosθ ,
问题:如果我们将公式中的力与位移类比推广到两个一
般向量,其结果又该如何表述?
?cos??? SFW
|| a || b ?cos??ba
功是力与位移的大小及其夹角余弦的乘积;
向量的数量积是两个向量的大小及其夹角余弦的乘积。
要点 1 平面向量数量积的概念
(1)数量积的定义
已知两个非零向量 a 和 b,它们的夹角为θ,则数量_______
叫做 a 与 b 的数量积(内积),记作 a·b,即 a·b=|a|·|b|cosθ.
_______叫做向量 a 在 b 方向上的投影.
(2)数量积的几何意义
数量积 a·b 等于|a|与________________________的乘积.
要点 2 平面向量数量积的性质及其运算律
(1)平面向量数量积的性质
若 a,b 是非零向量,则
①a⊥b?_________;
②若 a 与 b 同向,则 a·b=______;若 a 与 b 反向,则 a·b
=_______.
③a·a=|a|2或|a|=____.常用此性质进行实数与向量的转化.
④cosθ=______.
⑤|a·b|______|a||b|.
(2)平面向量数量积的运算律
①a·b=_____ (交换律);
②(λa)·b=_____=______ (数乘向量结合律);
③(a+b)·c=________ (分配律).
1.实数与向量的积与数量积有何区别?
2.当 a·b=0,则 a⊥b 对吗?
3.a·b=b·c?a=c,对吗?
4.(a·b)·c=a·(b·c)对吗?
1.实数与向量的积与数量积有何区别?
2.当 a·b=0,则 a⊥b 对吗?
答:实数与向量的积仍是向量;向量的数量积是实数,而不是
向量.
答:不对,也可能 a=0 或 b=0.
3.a·b=b·c?a=c,对吗?
答:不对,a·b=b·c?b·(a-c)=0?b⊥(a-c);或 b=0 或 a
=c.
4.(a·b)·c=a·(b·c)对吗?
答:不对,因为(a·b)·c 表示一个与 c 共线的向量,而 a·(b·c)表
示一个与 a 共线的向量,而 c 与 a 不一定共线.
5.一组常用公式
①(a+b)2=a2+2a·b+b2;
②(a-b)2=a2-2a·b+b2;
③(a+b)(a-b)=a2-b2;
④(a+b+c)2=a2+b2+c2+2a·b+2a·c+2b·c.
授 人 以 渔
题型一 数量积的运算
例 1 (1)已知|a|=2,|b|=5,若:①a∥b;②a⊥b;③a 与 b
的夹角为 30°,分别求 a·b.
【解析】 ①当 a∥b 时,若 a 与 b 同向,则它们的夹角为 0°.
∴a·b=|a||b|cos0°=2×5×1=10.
若 a 与 b 反向,则它们的夹角为 180°.
∴a·b=|a||b|cos180°=2×5×(-1)=-10.
②当 a⊥b 时,它们的夹角为 90°.
∴a·b=|a||b|cos90°=2×5×0=0.
③当 a 与 b 的夹角为 30°时,
a·b=|a||b|cos30°=2×5×
3
2
=5 3.
(2)已知点 A,B,C 满足|AB
→
|=3,|BC
→
|=4,|CA
→
|=5,则AB
→
·BC
→
+BC
→
·CA
→
+CA
→
·AB
→
的值是________.
AB
C
∟
【解析】 方法一:如图,根据题意可得△ABC
为直角三角形,且 B=
π
2
,cosA=
3
5
,cosC=
4
5
,
∴AB
→
·BC
→
+BC
→
·CA
→
+CA
→
·AB
→
=BC
→
·CA
→
+CA
→
·AB
→
=4×5cos(π-C)+5×3cos(π-A)
=-20cosC-15cosA
=-20×
4
5
-15×
3
5
=-25.
方法二:如图,建立平面直角坐标系,
则 A(3,0),B(0,0),C(0,4).
∴AB
→
=(-3,0),BC
→
=(0,4),CA
→
=(3,-
4).
∴AB
→
·BC
→
=-3×0+0×4=0,BC
→
·CA
→
=0×3+4×(-4)
=-16,CA
→
·AB
→
=3×(-3)+(-4)×0=-9.
∴AB
→
·BC
→
+BC
→
·CA
→
+CA
→
·AB
→
=-25.
探究 1 向量数量积的运算方法:
(1)当已知向量的模和夹角时,可利用定义法求解,即 a·b=
|a||b|cos〈a,b〉;
(2)注意共线时 θ=0°或 180°,垂直时 θ=90°,三种特殊
情况.
思考题 1 (1)已知 a,b 为单位向量,其夹角为 60°,则
(2a-b)·b=( )
A.-1 B.0
C.1 D.2
【解析】 由已知得|a|=|b|=1,〈a,b〉=60°,
∴(2a-b)·b=2a·b-b2=2|a||b|cos〈a,b〉-|b|2=2×1×1×cos60
°-12=0,故选 B.
【答案】 B
(2)已知正方形 ABCD 的边长为 2,E 为 CD 的中点,则AE
→
·BD
→
=________.
【解析】 AE
→
·BD
→
=
?
?
?
?
?
?
?
?
AD
→
+
1
2
AB
→
·(AD
→
-AB
→
)=AD
→ 2-
1
2
AB
→ 2=
2
2-
1
2
×22=2.
【答案】 2
A B
CD
E
题型二 向量的模
例 2 已知|a|=2,|b|=3,a 与 b 的夹角为 120°,求:
(1)a·b; (2)a2-b2; (3)|a+b|; (4)|a-b|.
【解析】 (1)a·b=|a||b|cos θ=2×3×cos 120°=-3.
(2)a
2-b2=|a|2-|b|2=4-9=-5.
(3)|a+b|= (a+b)2= a2+2a·b+b2
= |a|2+2|a||b|cosθ+|b|2
= 4-6+9= 7.
(4)|a-b|= (a-b)2=
a
2-2a·b+b2= 4+6+9= 19.
题型二 向量的模
例 2 已知|a|=2,|b|=3,a 与 b 的夹角为 120°,求:
(1)a·b; (2)a2-b2; (3)|a+b|; (4)|a-b|.
探究 2 对于向量的数量积的运算,有类似于多项式的运算
法则,但数量积不满足结合律,对于模的计算一般使用|a|= a2,
但|a·b|≠|a||b|,而是|a·b|≤|a||b|,因此在本例中第(4)小题不能如此
来解:
∵a2-b2=-5,∴|a2-b2|=5.
又|a+b|= 7,
∴|a-b|=
|a
2-b2|
|a+b|
=
5 7
7
.
这个结论显然错误.
思考题 2 (1)已知向量 a b 满足|a|=1,|b|=2,a 与 b 的
夹角为 60°,则|a-b|=________.
(2)已知|a|=3,|b|=2,a 与 b 的夹角为
π
6
.求 a·b,(2a+b)·b
和|a+b|.
思考题 2 (1)已知向量 a,b 满足|a|=1,|b|=2,a 与 b 的
夹角为 60°,则|a-b|=________.
【解析】 因为 |a- b|
2 = (a- b)2 = a2 - 2a·b + b2 = 12 -
2×1×2cos 60°+22=3,故|a-b|= 3.
【答案】 3
(2)已知|a|=3,|b|=2,a 与 b 的夹角为
π
6
.求 a·b,(2a+b)·b
和|a+b|.
【解析】 a·b=|a||b|cosθ=3×2×cos
π
6
=3 3,
(2a+b)·b=2a·b+b2=2×3 3+22=6 3+4,
|a+b|2=a2+2a·b+b2=13+6 3.
故|a+b|= 13+6 3.
题型三 向量的夹角
例 3 已知|a|=1,a·b=
1
2
,(a-b)·(a+b)=
1
2
,求:
(1)a 与 b 的夹角;
(2)a-b 与 a+b 的夹角的余弦值.
【思路分析】 解决本题的关键是求|b|,|a-b|和|a+b|的值,
然后运用夹角公式求出.
【解析】 (1)∵(a-b)·(a+b)=|a|2-|b|2=
1
2
,
又∵|a|=1,∴|b|=
2
2
.
设a与 b的夹角为 θ,则 cosθ=
a·b
|a|·|b|
=
1
2
1·
2
2
=
2
2
. ∴θ=45°.
(2)∵(a-b)2=a2-2a·b+b2=1-2×
1
2
+
1
2
=
1
2
,
∴|a-b|=
2
2
.
∵(a+b)2=a2+2a·b+b2=1+2×
1
2
+
1
2
=
5
2
,
∴|a+b|=
10
2
.
设 a-b 与 a+b 的夹角为 φ,
则 cosφ=
(a-b)·(a+b)
|a-b|·|a+b|
=
1
2
2
2
×
10
2
=
5
5
.∴cosφ=
5
5
.
探究 3 求两向量夹角的方法:
(1)一般是利用夹角公式:cosθ=
a·b
|a|·|b|
.
(2)注意:数量积大于 0 说明不共线的两向量的夹角为锐角,
数量积等于 0 说明两向量的夹角为直角,数量积小于 0 且两向量
不能共线时两向量的夹角为钝角.
(2)已知向量 a,b 满足(a+2b)·(a-b)=-6,且|a|=1,|b|
=2,则 a 与 b 的夹角为________.
思考题3 (1)已知|a|=8,|b|=5,|a+b|=7,求a与b的夹角θ.
【解析】 由|a+b|=7,得 a2+2a·b+b2=49.
∴a·b=-20.∴cosθ=
a·b
|a||b|
=-
1
2
即 θ=
2
3
π.
(2)已知向量 a,b 满足(a+2b)·(a-b)=-6,且|a|=1,|b|
=2,则 a 与 b 的夹角为________.
【解析】 设 a 与 b 的夹角为 θ,依题意有(a+2b)·(a-b)=a2
+a·b-2b2=-7+2cosθ=-6,所以 cosθ=
1
2
.因为 0≤θ≤π,所
以 θ=
π
3
.
思考题3 (1)已知|a|=8,|b|=5,|a+b|=7,求a与b的夹角θ.
用数量积求解垂直问题
例 1 已知非零向量 a,b,若 a+2b 与 a-2b 互相垂直,则
|a|
|b|
=________.
用数量积求解垂直问题
例 1 已知非零向量 a,b,若 a+2b 与 a-2b 互相垂直,则
|a|
|b|
=________.
【解析】 ∵(a+2b)·(a-2b)=a2-4b2=0,
∴|a|=2|b|,∴
|a|
|b|
=2.
【答案】 2
例 2 已知|a|=5,|b|=4,a 与 b 的夹角为 60°,问当 k 为
何值时,向量 ka-b 与 a+2b 垂直?
例 2 已知|a|=5,|b|=4,a 与 b 的夹角为 60°,问当 k 为
何值时,向量 ka-b 与 a+2b 垂直?
【解析】 (ka-b)·(a+2b)=ka2-a·b+2ka·b-2b2
=k|a|2-2|b|2-(1-2k)a·b
=25k-32-(1-2k)a·b
=25k-32-(1-2k)×5×4×cos60°=45k-42,
当 k=
14
15
时,45k-42=0,即(ka-b)·(a+2b)=0.
∴k=
14
15
时,(ka-b)⊥(a+2b).
题型四 数量积的几何意义
例 4 (1)已知|a|=6,e 为单位向量,当它们之间的夹角 θ 分
别等于 45°,90°,135°时,求出 a 在 e 方向上的投影,并画
图说明.
【思路分析】 a 在 e 方向上的投影为|a|·cosθ.
【解析】 如下图所示,当 θ=45°时,a 在 e 方向上的正
投影的数量为 3 2;
当 θ=90°时,a 在 e 方向上的投影的数量为 0;
当θ=135°时,a 在 e 方向上的投影的数量为-3 2.
∴|a|·cos45°=3 2,|a|·cos90°=0,
|a|·cos135°=-3 2.
(2)已知|a|=4,a 与 b 的夹角为 30°,则 a 在 b 方向上的投
影为________.
探究 4 数量积 a·b等于 a长度与 b在 a的方向上的投影|b|cos
θ乘积.
思考题 4 (1)已知|a|=3,|b|=4,a·b=-6.
①向量 a 在向量 b 方向上的投影为________.
②向量 b 在向量 a 方向上的投影为________.
(2)在边长为 2 的正三角形 ABC 中,AB
→
在BC
→
方向上的投影
为______.
课堂小结
5种题型(求数量积、模、夹角 数、投影)
4个性质
2个概念(数量积、投影)
3种运算(交换律、数乘结合律、分配律)
几个注意(数量积不是向量;投影不是长度;
数量积没有结合律、消去律)
这
一
节
课
1) 0a b a b? ? ? ?
cosa b a b ?? ?
? ?4
| || |
a b
a b
a b
? ?
?
)cos = 为 ,的夹角
3 | | | || |a b a b? ?)
2)︱a︱= ?a a
请做:课时作业(二十五)
2.4.1 平面向量数量积的物理
背景及其含义
向量的夹角
O A
B
?
已知两个非零向量 和 ,作 , ,则
叫做向量 和 的夹角.
OA a? OB b? ???AOB
)1800(
?? ??? a
ba
b
a
b
,a b记作
复习
问 题
θ
s
F
一个物体在力F 的作用下产生的位移 s ,
那么力F 所做的功应当怎样计算?
为此,我们引入向量“数量积”的概念。
功是一个标量,它由力和位移两个矢量(向量)来确定.
这给我们一种启示,能否把“功”看成是这两个向量的一种运
算的结果呢?
其中θ是 F 与 s 的夹角 .W = |F||s| cosθ ,
问题:如果我们将公式中的力与位移类比推广到两个一
般向量,其结果又该如何表述?
?cos??? SFW
|| a || b ?cos??ba
功是力与位移的大小及其夹角余弦的乘积;
向量的数量积是两个向量的大小及其夹角余弦的乘积。
要点 1 平面向量数量积的概念
(1)数量积的定义
已知两个非零向量 a 和 b,它们的夹角为θ,则数量_______
叫做 a 与 b 的数量积(内积),记作 a·b,即 a·b=|a|·|b|cosθ.
_______叫做向量 a 在 b 方向上的投影.
(2)数量积的几何意义
数量积 a·b 等于|a|与________________________的乘积.
要点 2 平面向量数量积的性质及其运算律
(1)平面向量数量积的性质
若 a,b 是非零向量,则
①a⊥b?_________;
②若 a 与 b 同向,则 a·b=______;若 a 与 b 反向,则 a·b
=_______.
③a·a=|a|2或|a|=____.常用此性质进行实数与向量的转化.
④cosθ=______.
⑤|a·b|______|a||b|.
(2)平面向量数量积的运算律
①a·b=_____ (交换律);
②(λa)·b=_____=______ (数乘向量结合律);
③(a+b)·c=________ (分配律).
1.实数与向量的积与数量积有何区别?
2.当 a·b=0,则 a⊥b 对吗?
3.a·b=b·c?a=c,对吗?
4.(a·b)·c=a·(b·c)对吗?
1.实数与向量的积与数量积有何区别?
2.当 a·b=0,则 a⊥b 对吗?
答:实数与向量的积仍是向量;向量的数量积是实数,而不是
向量.
答:不对,也可能 a=0 或 b=0.
3.a·b=b·c?a=c,对吗?
答:不对,a·b=b·c?b·(a-c)=0?b⊥(a-c);或 b=0 或 a
=c.
4.(a·b)·c=a·(b·c)对吗?
答:不对,因为(a·b)·c 表示一个与 c 共线的向量,而 a·(b·c)表
示一个与 a 共线的向量,而 c 与 a 不一定共线.
5.一组常用公式
①(a+b)2=a2+2a·b+b2;
②(a-b)2=a2-2a·b+b2;
③(a+b)(a-b)=a2-b2;
④(a+b+c)2=a2+b2+c2+2a·b+2a·c+2b·c.
授 人 以 渔
题型一 数量积的运算
例 1 (1)已知|a|=2,|b|=5,若:①a∥b;②a⊥b;③a 与 b
的夹角为 30°,分别求 a·b.
【解析】 ①当 a∥b 时,若 a 与 b 同向,则它们的夹角为 0°.
∴a·b=|a||b|cos0°=2×5×1=10.
若 a 与 b 反向,则它们的夹角为 180°.
∴a·b=|a||b|cos180°=2×5×(-1)=-10.
②当 a⊥b 时,它们的夹角为 90°.
∴a·b=|a||b|cos90°=2×5×0=0.
③当 a 与 b 的夹角为 30°时,
a·b=|a||b|cos30°=2×5×
3
2
=5 3.
(2)已知点 A,B,C 满足|AB
→
|=3,|BC
→
|=4,|CA
→
|=5,则AB
→
·BC
→
+BC
→
·CA
→
+CA
→
·AB
→
的值是________.
AB
C
∟
【解析】 方法一:如图,根据题意可得△ABC
为直角三角形,且 B=
π
2
,cosA=
3
5
,cosC=
4
5
,
∴AB
→
·BC
→
+BC
→
·CA
→
+CA
→
·AB
→
=BC
→
·CA
→
+CA
→
·AB
→
=4×5cos(π-C)+5×3cos(π-A)
=-20cosC-15cosA
=-20×
4
5
-15×
3
5
=-25.
方法二:如图,建立平面直角坐标系,
则 A(3,0),B(0,0),C(0,4).
∴AB
→
=(-3,0),BC
→
=(0,4),CA
→
=(3,-
4).
∴AB
→
·BC
→
=-3×0+0×4=0,BC
→
·CA
→
=0×3+4×(-4)
=-16,CA
→
·AB
→
=3×(-3)+(-4)×0=-9.
∴AB
→
·BC
→
+BC
→
·CA
→
+CA
→
·AB
→
=-25.
探究 1 向量数量积的运算方法:
(1)当已知向量的模和夹角时,可利用定义法求解,即 a·b=
|a||b|cos〈a,b〉;
(2)注意共线时 θ=0°或 180°,垂直时 θ=90°,三种特殊
情况.
思考题 1 (1)已知 a,b 为单位向量,其夹角为 60°,则
(2a-b)·b=( )
A.-1 B.0
C.1 D.2
【解析】 由已知得|a|=|b|=1,〈a,b〉=60°,
∴(2a-b)·b=2a·b-b2=2|a||b|cos〈a,b〉-|b|2=2×1×1×cos60
°-12=0,故选 B.
【答案】 B
(2)已知正方形 ABCD 的边长为 2,E 为 CD 的中点,则AE
→
·BD
→
=________.
【解析】 AE
→
·BD
→
=
?
?
?
?
?
?
?
?
AD
→
+
1
2
AB
→
·(AD
→
-AB
→
)=AD
→ 2-
1
2
AB
→ 2=
2
2-
1
2
×22=2.
【答案】 2
A B
CD
E
题型二 向量的模
例 2 已知|a|=2,|b|=3,a 与 b 的夹角为 120°,求:
(1)a·b; (2)a2-b2; (3)|a+b|; (4)|a-b|.
【解析】 (1)a·b=|a||b|cos θ=2×3×cos 120°=-3.
(2)a
2-b2=|a|2-|b|2=4-9=-5.
(3)|a+b|= (a+b)2= a2+2a·b+b2
= |a|2+2|a||b|cosθ+|b|2
= 4-6+9= 7.
(4)|a-b|= (a-b)2=
a
2-2a·b+b2= 4+6+9= 19.
题型二 向量的模
例 2 已知|a|=2,|b|=3,a 与 b 的夹角为 120°,求:
(1)a·b; (2)a2-b2; (3)|a+b|; (4)|a-b|.
探究 2 对于向量的数量积的运算,有类似于多项式的运算
法则,但数量积不满足结合律,对于模的计算一般使用|a|= a2,
但|a·b|≠|a||b|,而是|a·b|≤|a||b|,因此在本例中第(4)小题不能如此
来解:
∵a2-b2=-5,∴|a2-b2|=5.
又|a+b|= 7,
∴|a-b|=
|a
2-b2|
|a+b|
=
5 7
7
.
这个结论显然错误.
思考题 2 (1)已知向量 a b 满足|a|=1,|b|=2,a 与 b 的
夹角为 60°,则|a-b|=________.
(2)已知|a|=3,|b|=2,a 与 b 的夹角为
π
6
.求 a·b,(2a+b)·b
和|a+b|.
思考题 2 (1)已知向量 a,b 满足|a|=1,|b|=2,a 与 b 的
夹角为 60°,则|a-b|=________.
【解析】 因为 |a- b|
2 = (a- b)2 = a2 - 2a·b + b2 = 12 -
2×1×2cos 60°+22=3,故|a-b|= 3.
【答案】 3
(2)已知|a|=3,|b|=2,a 与 b 的夹角为
π
6
.求 a·b,(2a+b)·b
和|a+b|.
【解析】 a·b=|a||b|cosθ=3×2×cos
π
6
=3 3,
(2a+b)·b=2a·b+b2=2×3 3+22=6 3+4,
|a+b|2=a2+2a·b+b2=13+6 3.
故|a+b|= 13+6 3.
题型三 向量的夹角
例 3 已知|a|=1,a·b=
1
2
,(a-b)·(a+b)=
1
2
,求:
(1)a 与 b 的夹角;
(2)a-b 与 a+b 的夹角的余弦值.
【思路分析】 解决本题的关键是求|b|,|a-b|和|a+b|的值,
然后运用夹角公式求出.
【解析】 (1)∵(a-b)·(a+b)=|a|2-|b|2=
1
2
,
又∵|a|=1,∴|b|=
2
2
.
设a与 b的夹角为 θ,则 cosθ=
a·b
|a|·|b|
=
1
2
1·
2
2
=
2
2
. ∴θ=45°.
(2)∵(a-b)2=a2-2a·b+b2=1-2×
1
2
+
1
2
=
1
2
,
∴|a-b|=
2
2
.
∵(a+b)2=a2+2a·b+b2=1+2×
1
2
+
1
2
=
5
2
,
∴|a+b|=
10
2
.
设 a-b 与 a+b 的夹角为 φ,
则 cosφ=
(a-b)·(a+b)
|a-b|·|a+b|
=
1
2
2
2
×
10
2
=
5
5
.∴cosφ=
5
5
.
探究 3 求两向量夹角的方法:
(1)一般是利用夹角公式:cosθ=
a·b
|a|·|b|
.
(2)注意:数量积大于 0 说明不共线的两向量的夹角为锐角,
数量积等于 0 说明两向量的夹角为直角,数量积小于 0 且两向量
不能共线时两向量的夹角为钝角.
(2)已知向量 a,b 满足(a+2b)·(a-b)=-6,且|a|=1,|b|
=2,则 a 与 b 的夹角为________.
思考题3 (1)已知|a|=8,|b|=5,|a+b|=7,求a与b的夹角θ.
【解析】 由|a+b|=7,得 a2+2a·b+b2=49.
∴a·b=-20.∴cosθ=
a·b
|a||b|
=-
1
2
即 θ=
2
3
π.
(2)已知向量 a,b 满足(a+2b)·(a-b)=-6,且|a|=1,|b|
=2,则 a 与 b 的夹角为________.
【解析】 设 a 与 b 的夹角为 θ,依题意有(a+2b)·(a-b)=a2
+a·b-2b2=-7+2cosθ=-6,所以 cosθ=
1
2
.因为 0≤θ≤π,所
以 θ=
π
3
.
思考题3 (1)已知|a|=8,|b|=5,|a+b|=7,求a与b的夹角θ.
用数量积求解垂直问题
例 1 已知非零向量 a,b,若 a+2b 与 a-2b 互相垂直,则
|a|
|b|
=________.
用数量积求解垂直问题
例 1 已知非零向量 a,b,若 a+2b 与 a-2b 互相垂直,则
|a|
|b|
=________.
【解析】 ∵(a+2b)·(a-2b)=a2-4b2=0,
∴|a|=2|b|,∴
|a|
|b|
=2.
【答案】 2
例 2 已知|a|=5,|b|=4,a 与 b 的夹角为 60°,问当 k 为
何值时,向量 ka-b 与 a+2b 垂直?
例 2 已知|a|=5,|b|=4,a 与 b 的夹角为 60°,问当 k 为
何值时,向量 ka-b 与 a+2b 垂直?
【解析】 (ka-b)·(a+2b)=ka2-a·b+2ka·b-2b2
=k|a|2-2|b|2-(1-2k)a·b
=25k-32-(1-2k)a·b
=25k-32-(1-2k)×5×4×cos60°=45k-42,
当 k=
14
15
时,45k-42=0,即(ka-b)·(a+2b)=0.
∴k=
14
15
时,(ka-b)⊥(a+2b).
题型四 数量积的几何意义
例 4 (1)已知|a|=6,e 为单位向量,当它们之间的夹角 θ 分
别等于 45°,90°,135°时,求出 a 在 e 方向上的投影,并画
图说明.
【思路分析】 a 在 e 方向上的投影为|a|·cosθ.
【解析】 如下图所示,当 θ=45°时,a 在 e 方向上的正
投影的数量为 3 2;
当 θ=90°时,a 在 e 方向上的投影的数量为 0;
当θ=135°时,a 在 e 方向上的投影的数量为-3 2.
∴|a|·cos45°=3 2,|a|·cos90°=0,
|a|·cos135°=-3 2.
(2)已知|a|=4,a 与 b 的夹角为 30°,则 a 在 b 方向上的投
影为________.
探究 4 数量积 a·b等于 a长度与 b在 a的方向上的投影|b|cos
θ乘积.
思考题 4 (1)已知|a|=3,|b|=4,a·b=-6.
①向量 a 在向量 b 方向上的投影为________.
②向量 b 在向量 a 方向上的投影为________.
(2)在边长为 2 的正三角形 ABC 中,AB
→
在BC
→
方向上的投影
为______.
课堂小结
5种题型(求数量积、模、夹角 数、投影)
4个性质
2个概念(数量积、投影)
3种运算(交换律、数乘结合律、分配律)
几个注意(数量积不是向量;投影不是长度;
数量积没有结合律、消去律)
这
一
节
课
1) 0a b a b? ? ? ?
cosa b a b ?? ?
? ?4
| || |
a b
a b
a b
? ?
?
)cos = 为 ,的夹角
3 | | | || |a b a b? ?)
2)︱a︱= ?a a
请做:课时作业(二十五)
