人教A版高中数学选修2-2《1.1.3导数的几何意义》课件(共18张PPT)
文档属性
| 名称 | 人教A版高中数学选修2-2《1.1.3导数的几何意义》课件(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 665.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-03 00:00:00 | ||
图片预览



文档简介
(共18张PPT)
1.1.3导数的几何意义
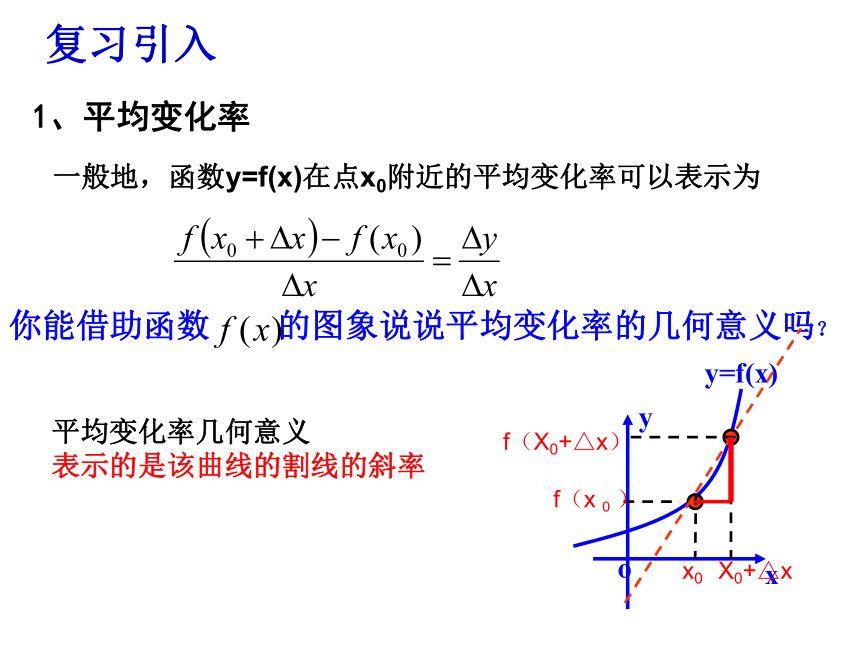
1、平均变化率
一般地,函数y=f(x)在点x0附近的平均变化率可以表示为
复习引入
平均变化率几何意义
表示的是该曲线的割线的斜率
2.导数的概念
从代数的角度:
当△x→0时,割线PQ的斜率的极限,
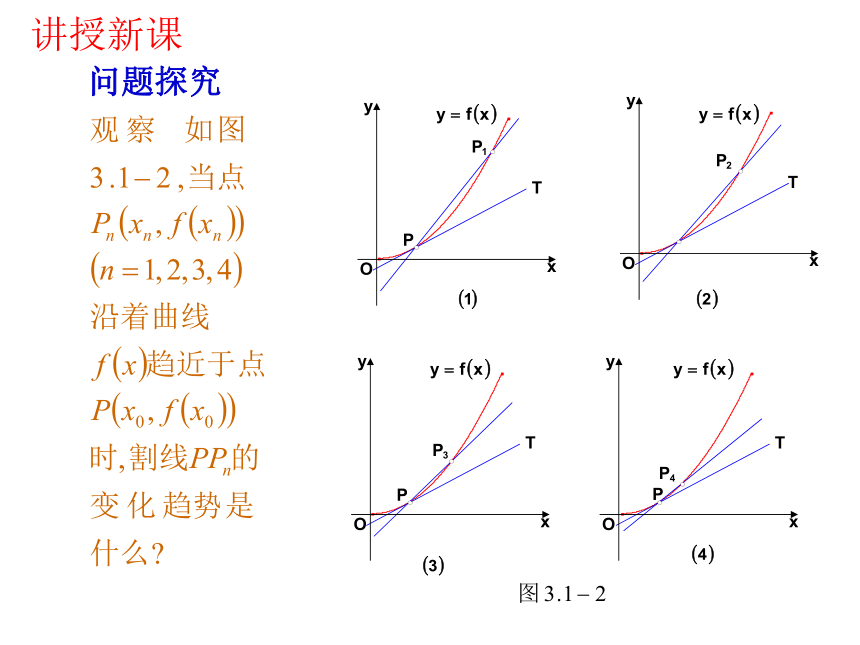
问题探究
讲授新课
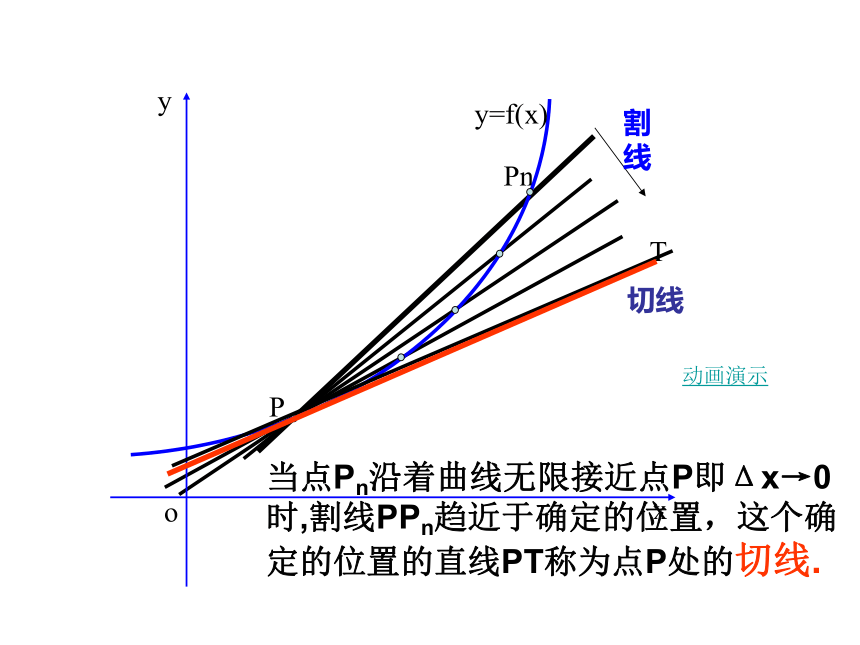
切线
当点Pn沿着曲线无限接近点P即Δx→0时,割线PPn趋近于确定的位置,这个确定的位置的直线PT称为点P处的切线.
动画演示
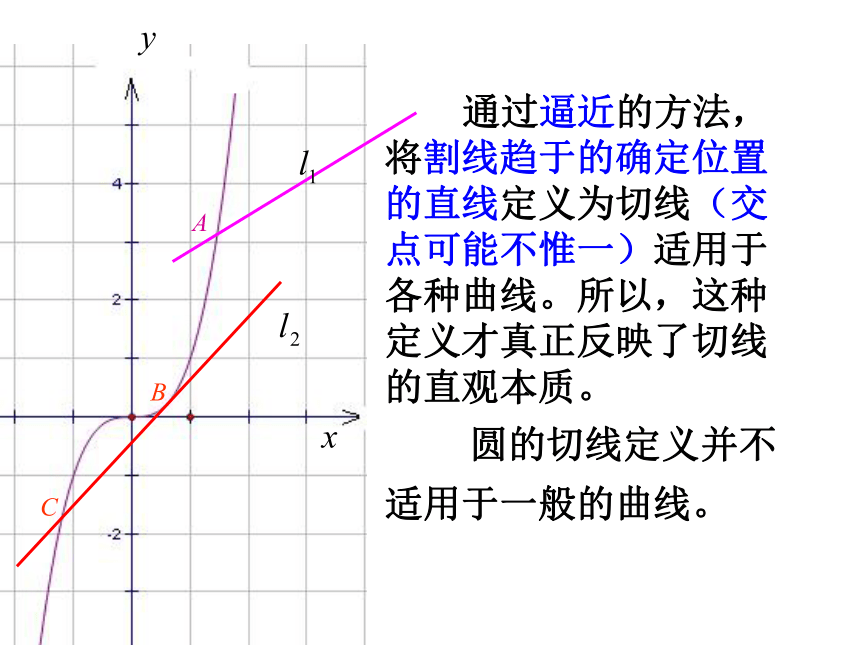
通过逼近的方法,将割线趋于的确定位置的直线定义为切线(交点可能不惟一)适用于各种曲线。所以,这种定义才真正反映了切线的直观本质。
圆的切线定义并不适用于一般的曲线。
大多数函数曲线就一小范围来看,大致可看作直线,所以,某点附近的曲线可以用过此点的切线近似代替,即“以直代曲” (以简单的对象刻画复杂的对象)的思想方法.
M
△x
△y
割线的斜率与切线的斜率有什么关系呢?
即:当△x→0时,割线PQ的斜率的极限,就是曲线在点P处的切线的斜率,
合作交流
导数的几何意义
归纳小结
典例精讲
动画演示
例2:
-2
典例精讲
(3)在曲线y=x2上切线倾斜角为π/ 4的切点是( )
A.(0,0) B.(2,4) C.(1/4,1/6 ) D.(1/2,1/4 )
D
(2)设曲线y=ax2在点(1,a)处的切线与直线
2x-y-6=0平行,则a等于_______.
1
动画演示
拓展提升:
例1:求曲线y=x2+1在点P(1,2)处 的切线方程.
动画演示
当堂检测:
B
2.已知曲线y=2x2上的点(1,2),求过该点且与过该点的切线垂直的直线方程.
x+4y-9=0
3、求切线方程的步骤:
总结
1、导数的几何意义:
2、切线的斜率:
4.求曲线的切线方程时,要注意区分“过”一点与“在”某点求切线问题
无限逼近的极限思想、以直代曲的思想以及数形结合的思想。
5. 三种数学思想
课后作业
习题1.1 A组 第5、6题
1.1.3导数的几何意义
1、平均变化率
一般地,函数y=f(x)在点x0附近的平均变化率可以表示为
复习引入
平均变化率几何意义
表示的是该曲线的割线的斜率
2.导数的概念
从代数的角度:
当△x→0时,割线PQ的斜率的极限,
问题探究
讲授新课
切线
当点Pn沿着曲线无限接近点P即Δx→0时,割线PPn趋近于确定的位置,这个确定的位置的直线PT称为点P处的切线.
动画演示
通过逼近的方法,将割线趋于的确定位置的直线定义为切线(交点可能不惟一)适用于各种曲线。所以,这种定义才真正反映了切线的直观本质。
圆的切线定义并不适用于一般的曲线。
大多数函数曲线就一小范围来看,大致可看作直线,所以,某点附近的曲线可以用过此点的切线近似代替,即“以直代曲” (以简单的对象刻画复杂的对象)的思想方法.
M
△x
△y
割线的斜率与切线的斜率有什么关系呢?
即:当△x→0时,割线PQ的斜率的极限,就是曲线在点P处的切线的斜率,
合作交流
导数的几何意义
归纳小结
典例精讲
动画演示
例2:
-2
典例精讲
(3)在曲线y=x2上切线倾斜角为π/ 4的切点是( )
A.(0,0) B.(2,4) C.(1/4,1/6 ) D.(1/2,1/4 )
D
(2)设曲线y=ax2在点(1,a)处的切线与直线
2x-y-6=0平行,则a等于_______.
1
动画演示
拓展提升:
例1:求曲线y=x2+1在点P(1,2)处 的切线方程.
动画演示
当堂检测:
B
2.已知曲线y=2x2上的点(1,2),求过该点且与过该点的切线垂直的直线方程.
x+4y-9=0
3、求切线方程的步骤:
总结
1、导数的几何意义:
2、切线的斜率:
4.求曲线的切线方程时,要注意区分“过”一点与“在”某点求切线问题
无限逼近的极限思想、以直代曲的思想以及数形结合的思想。
5. 三种数学思想
课后作业
习题1.1 A组 第5、6题
