必修2第一章 空间几何体多面体与球体的切接问题 课件 23张PPT
文档属性
| 名称 | 必修2第一章 空间几何体多面体与球体的切接问题 课件 23张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 796.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-04 00:00:00 | ||
图片预览








文档简介
(共23张PPT)
多面体与球体的切接问题
限时训练答题情况:
优秀个人:解梦雪 霍晨辉 宋 良 崔 颖
张宇赟 娄苗苗 郭慧慧 苗 圃 景晓娜
李塞楠 田亚楠 李佳乐 宋云飞
优秀小组:第2组 第6组 第5组
1---12题正答情况统计
出错较多的题目:5 9 10 11 12
存在的主要问题:
1.数形结合思想运用不到位;
2.球体的切接问题不熟练;
3.题解不规范,不注意细节。
题号 1 2 3 4 5 6 7 8 9 10 11 12
答错人数 1 2 2 3 15 7 3 2 13 15 30 31
学习目标
1、用最快的速度,最简单的方法完成。
2、掌握数形结合思想,转化思想。
3、熟练的掌握各种题型,记住一些重要的结论。
高考回放
多面体与球体的切接
2013年全国Ⅰ卷(理)
2015年全国Ⅱ卷(理)
2016年全国Ⅲ卷(理)
2017年全国Ⅰ卷(文)
2018年全国三卷(理)
2019年全国一卷(理)
基本知识回顾:
二、球与多面体的接、切
定义1:若一个多面体的各顶点都在一个球的球面上, 则称这个多面体是这个球的内接多面体, 这个球是这个 。
定义2:若一个多面体的各面都与一个球的球面相切, 则称这个多面体是这个球的外切多面体, 这个球是这个 。
多面体的外接球
多面体的内切球
外接球球心到各顶点的距离相等(R)
内切球球心到各面的距离相等(r)
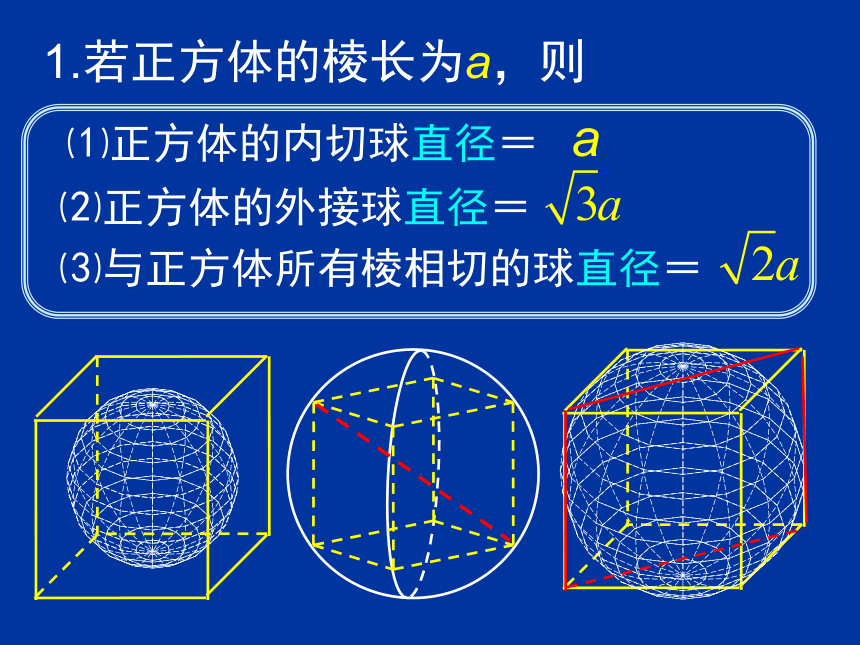
⑴正方体的内切球直径=
⑵正方体的外接球直径=
⑶与正方体所有棱相切的球直径=
1.若正方体的棱长为a,则
a
2.长方体外接球:
3.直棱柱的外接球半径
(1)先找外接球的球心:
它的球心是连接上下两个多边形的外心的线段的中点;
(2) 再构造直角三角形,勾股定理求解
二、棱锥与球
正四面体ABCD的棱长为a,求其内切球半径r与外接球半径R.
难点突破:如何求正四面体的外接球半径
法1.补成正方体
P
A
B
C
M
O
D
法2.勾股定理法
难点突破:如何求正四面体的外接球半径
求棱锥外接球半径的方法:
(1)补形法(适用特殊棱锥)
三条侧棱两两垂直的三棱锥常补成长方体;
三组对棱分别相等的三棱锥可补成长方体;
侧棱垂直底面的棱锥可补成直棱柱
(2)勾股定理法 (通法)
关键是找球心,球心一定在过底面的外心与底面垂直的直线上,画出截面图,构造与R有关的直角三角形。
求棱锥内切球半径的方法:等体积法
自我纠错(时间5分钟)
要求:1、结合所学知识,独立思考,自查自纠;
2、根据高考要求总结题型,进一步完善知识网络。
设疑自探:
自探一: 测试卷11
自探二:测试卷12
要求:
(1)请各位同学积极把你的观点在组内展示,小组长要认真组织,确保人人参与热烈讨论。
(2)请汇集全组智慧,找出最能代表你们聪明才智的答案,并认真做好结论的归纳升华。
(3)注意展示点评任务,展示人书写要迅速。
小组讨论
在展示评价后,若你仍有补充,我们奖励 分
20
题 号 方 式 展示分工
自探一 板书 第五组
自探二 板书 第三组
质疑再探
变式:
C
运用拓展
B
4.(2018·课标全国3改编)设A,B,C,D是同一个半径为4的球的球 面上四点, 为等边三角形且其面积为 , 则三棱锥D-ABC的高为
2或6 。
5.(2019年全国1卷12题)已知三棱锥P-ABC的四个顶点在球O的球面上,PA=PB=PC,三角形ABC是边长为2的正三角形,E,F分别是PA,AB的中点,且 ,则球O的体积为( )
A. B. C. D.
D
总结本节课内容,重点,难点!
学科班长总结本节课同学们的表现!
多面体与球体的切接问题
限时训练答题情况:
优秀个人:解梦雪 霍晨辉 宋 良 崔 颖
张宇赟 娄苗苗 郭慧慧 苗 圃 景晓娜
李塞楠 田亚楠 李佳乐 宋云飞
优秀小组:第2组 第6组 第5组
1---12题正答情况统计
出错较多的题目:5 9 10 11 12
存在的主要问题:
1.数形结合思想运用不到位;
2.球体的切接问题不熟练;
3.题解不规范,不注意细节。
题号 1 2 3 4 5 6 7 8 9 10 11 12
答错人数 1 2 2 3 15 7 3 2 13 15 30 31
学习目标
1、用最快的速度,最简单的方法完成。
2、掌握数形结合思想,转化思想。
3、熟练的掌握各种题型,记住一些重要的结论。
高考回放
多面体与球体的切接
2013年全国Ⅰ卷(理)
2015年全国Ⅱ卷(理)
2016年全国Ⅲ卷(理)
2017年全国Ⅰ卷(文)
2018年全国三卷(理)
2019年全国一卷(理)
基本知识回顾:
二、球与多面体的接、切
定义1:若一个多面体的各顶点都在一个球的球面上, 则称这个多面体是这个球的内接多面体, 这个球是这个 。
定义2:若一个多面体的各面都与一个球的球面相切, 则称这个多面体是这个球的外切多面体, 这个球是这个 。
多面体的外接球
多面体的内切球
外接球球心到各顶点的距离相等(R)
内切球球心到各面的距离相等(r)
⑴正方体的内切球直径=
⑵正方体的外接球直径=
⑶与正方体所有棱相切的球直径=
1.若正方体的棱长为a,则
a
2.长方体外接球:
3.直棱柱的外接球半径
(1)先找外接球的球心:
它的球心是连接上下两个多边形的外心的线段的中点;
(2) 再构造直角三角形,勾股定理求解
二、棱锥与球
正四面体ABCD的棱长为a,求其内切球半径r与外接球半径R.
难点突破:如何求正四面体的外接球半径
法1.补成正方体
P
A
B
C
M
O
D
法2.勾股定理法
难点突破:如何求正四面体的外接球半径
求棱锥外接球半径的方法:
(1)补形法(适用特殊棱锥)
三条侧棱两两垂直的三棱锥常补成长方体;
三组对棱分别相等的三棱锥可补成长方体;
侧棱垂直底面的棱锥可补成直棱柱
(2)勾股定理法 (通法)
关键是找球心,球心一定在过底面的外心与底面垂直的直线上,画出截面图,构造与R有关的直角三角形。
求棱锥内切球半径的方法:等体积法
自我纠错(时间5分钟)
要求:1、结合所学知识,独立思考,自查自纠;
2、根据高考要求总结题型,进一步完善知识网络。
设疑自探:
自探一: 测试卷11
自探二:测试卷12
要求:
(1)请各位同学积极把你的观点在组内展示,小组长要认真组织,确保人人参与热烈讨论。
(2)请汇集全组智慧,找出最能代表你们聪明才智的答案,并认真做好结论的归纳升华。
(3)注意展示点评任务,展示人书写要迅速。
小组讨论
在展示评价后,若你仍有补充,我们奖励 分
20
题 号 方 式 展示分工
自探一 板书 第五组
自探二 板书 第三组
质疑再探
变式:
C
运用拓展
B
4.(2018·课标全国3改编)设A,B,C,D是同一个半径为4的球的球 面上四点, 为等边三角形且其面积为 , 则三棱锥D-ABC的高为
2或6 。
5.(2019年全国1卷12题)已知三棱锥P-ABC的四个顶点在球O的球面上,PA=PB=PC,三角形ABC是边长为2的正三角形,E,F分别是PA,AB的中点,且 ,则球O的体积为( )
A. B. C. D.
D
总结本节课内容,重点,难点!
学科班长总结本节课同学们的表现!
