苏教版高中数学必修一教学讲义,复习补习资料(含知识讲解,巩固练习):29函数与方程(基础)
文档属性
| 名称 | 苏教版高中数学必修一教学讲义,复习补习资料(含知识讲解,巩固练习):29函数与方程(基础) |

|
|
| 格式 | zip | ||
| 文件大小 | 289.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-05 00:00:00 | ||
图片预览




文档简介
函数与方程
【学习目标】
(1)重点理解函数零点的概念,判定二次函数零点的个数,会求函数的零点;
(2)结合二次函数的图象,判断一元二次方程根的存在性及根的个数,从而了解函数零点与方程根的联系;
(3)根据具体函数的图象,能够借助计算器用二分法求函数零点的近似解,了解这种方法是求函数零点近似解的常用方法.
【经典例题】
类型一、求函数的零点
例1.已知函数.
(1)解方程(x+3)(x+1)(x―2)=0;
(2)画出函数的图象(简图),并求出函数的零点;
(3)讨论函数在零点两侧的函数值的正负.
【解析】(1)方程有三个根x1=―3,x2=―1,x3=2.
(2)函数的图象如右图,零点为―3,―1,2.
(3)由函数的图象可以直观地看出,在函数的零点―3左侧的函数值为负,在零点―3的右侧与零点―1的左侧的函数值为正,零点―1的右侧与零点2的左侧的函数值为负,零点2右侧的函数值为正.
【总结升华】(1)方程(x+3)(x+1)(x―2)=0左边是三个因式的积的形式,只要有一个因式为0,方程就成立,所以x+3=0或x+1=0或x―2=0,所以x=―3或x=―1或x=2;
(2)可以用描点的方法画出函数图象的简图;
(3)在x轴的上方,纵坐标为正,相应的函数值就为正;在x轴的下方,纵坐标为负,相应的函数值就为负.
举一反三:
【变式1】已知函数,且m,n是方程的两个根(m<n),则实数a、b、m、n的大小关系可能是( )
A.m<a<b<n B.a<m<n<b C.m<a<n<b D.a<m<b<n
【答案】 B
【解析】由函数,我们可以看到a、b为的零点,且,如右图,则应有a<m<n<b,故选B.
例2. 求下列函数的零点.
(1);
(2).
【答案】(1);(2)-1,1.
【解析】根据函数零点与方程的根之间的关系,要求函数的零点,就是求相应方程的实数根.
(1)由得,所以函数的零点是;
(2)由,令得x=1,-1,故函数的零点是-1,1.
【总结升华】求函数的零点就是求相应方程的实数根,一般可以借助求根公式或因式分解等方法,求出方程的根,从而得到函数的零点.
举一反三:
【变式1】求函数:(1);(2)的零点.
【答案】(1)-3,1;(2)-3,1,2.
【解析】(1)由求根公式解得
(2)方程可化为
由知
所以函数的零点为-3,1;函数的零点为-3,1,2.
【总结升华】三次因式分解的关键是,裂项后的两组分别要有公因式可提取,函数求零点的题目和解方程的题目可相互转化.
类型二、函数零点的存在性定理
例3.已知函数,问:方程在区间内有没有实数根?为什么?
【答案】没有实数根
【解析】先求出及的值,进而确定和的符号,当它们其中一个值小于零另一个值大于零时,便可确定在上有实数根.
,
且函数的图象是连续曲线,
在区间内有实数根
【总结升华】利用函数零点的存在性定理可以判断方程在某区间内是否有实数根,是利用计算机求方程近似根的重要依据,因此必须熟练掌握这个定理.需要注意的是,方程在区间内有实数根,不一定有.
举一反三:
【变式1】判断下列函数在给定区间上是否存在零点:
(1)
(2);
【答案】(1)存在;(2)存在;(3)存在.
【解析】(1)
故在上存在零点.
(2)
故在区间上存在零点.
【变式2】若函数,则下列判断正确的是( )
A.方程f(x)=0在区间[0,1]内一定有解
B.方程f(x)=0在区间[0,1]内一定无解
C.函数f(x)是奇函数
D.函数f(x)是偶函数
【答案】A
类型三、一元二次方程根的分布
例4. 已知关于x的二次方程x2+2mx+2m+1=0.
(1)若方程有两根,其中一根在区间(―1,0)和(1,2)内,求的取值范围.
(2)若方程两根均在区间(0,1)内,求的取值范围.
【答案】(1);(2).
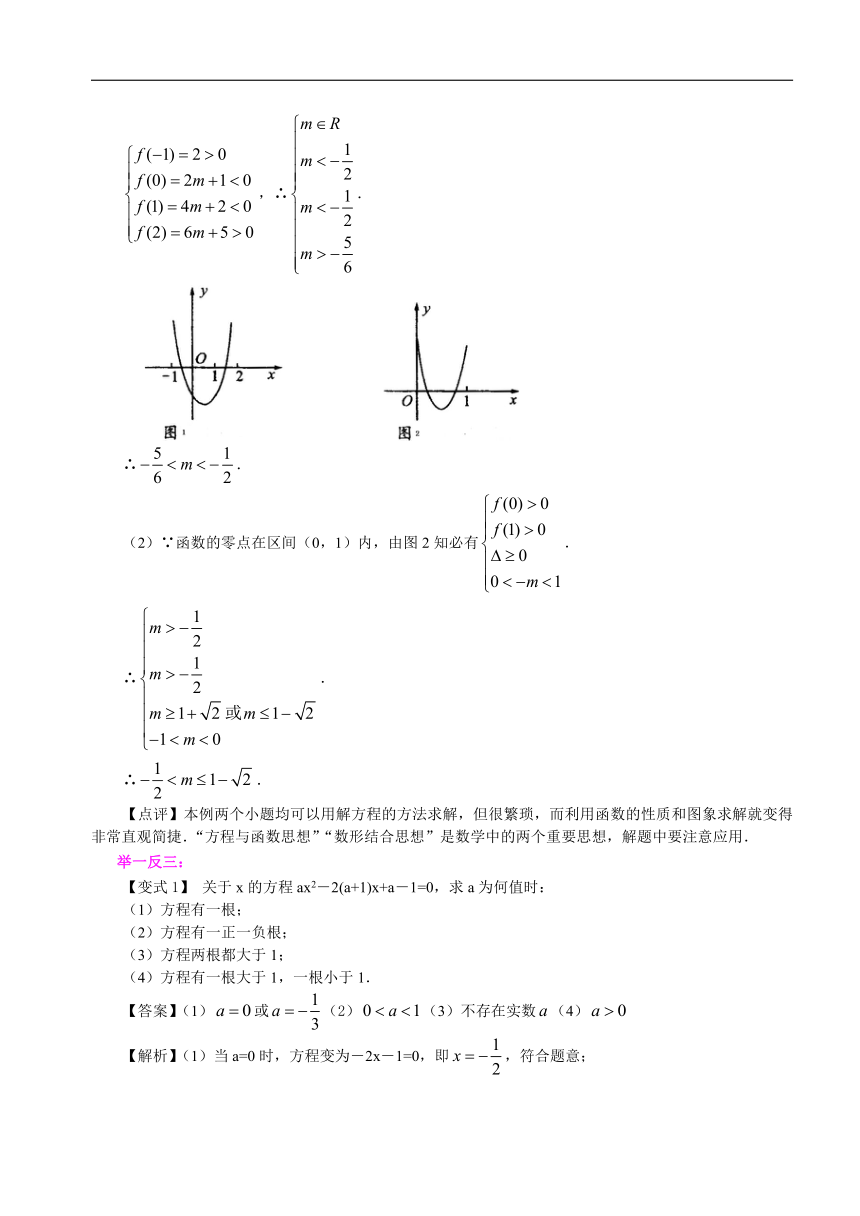
【解析】 (1)条件说明函数的零点在区间(-1,0)和(1,2)内,由图1可知,
,∴.
∴.
(2)∵函数的零点在区间(0,1)内,由图2知必有.
∴.
∴.
【点评】本例两个小题均可以用解方程的方法求解,但很繁琐,而利用函数的性质和图象求解就变得非常直观简捷.“方程与函数思想”“数形结合思想”是数学中的两个重要思想,解题中要注意应用.
举一反三:
【变式1】 关于x的方程ax2―2(a+1)x+a―1=0,求a为何值时:
(1)方程有一根;
(2)方程有一正一负根;
(3)方程两根都大于1;
(4)方程有一根大于1,一根小于1.
【答案】(1)或(2)(3)不存在实数(4)
【解析】(1)当a=0时,方程变为―2x―1=0,即,符合题意;
当时,方程为二次方程,因为方程有一根,所以,解得.综上可知,当或时,关于的方程ax2―2(a+1)x+a―1=0有一根.
(2)因为方程有一正一负根,所以由根与系数的关系得.又解得.
(3)方程两根都大于1,图象大致如图
所以必须满足
或两不等式组均无解.
所以不存在实数,使方程两根都大于1.
(4)因为方程有一根大于1,一根小于1,图象大致如图
所以必须满足或解得.
类型四、用二分法求函数的零点的近似值
例5.求函数的一个正数零点(精确到0.1).
【答案】1.7
【解析】由于,可取区间作为计算的初始区间,用二分法逐步计算,列表如下:
区间
中点
中点函数值
[1,2]
1.5
-2.625
[1.5,2]
1.75
0.2344
[1.5,1.75]
1.625
-1.3027
[1.625,1.75]
1.6875
-0.5618
[1.6875,1.75]
1.71875
-0.1709
由上表计算可知,区间[1.6875,1.75]的长度1.75-1.6875=0.0625<0.1,所以可以将1.6875的近似值1.7作为函数零点的近似值.
【总结升华】应首先判断x的取正整数时,函数值的正负,使正整数所对应的区间尽量小,便于利用二分法求其近似值.
举一反三:
【变式1】若函数的一个正数零点附近的函数值
用二分法计算,其参考数据如下:
f(1)=-2
f(1.5)=0.625
f(1.25)=-0.984
f(1.375)=-0.260
f(1.4375)=0. 162
f(1.40625)=-0. 054
那么方程的一个近似根(精确到0.1)为( )
A.1.2 B.1.3 C.1.4 D.1.5
【答案】C
【变式2】用二分法求函数的一个正零点(精确到)
【答案】2.24
【解析】⑴由,可知函数的一个正零点在区间中;
⑵取的区间中点;
⑶计算;
⑷由于,则有零点的新区间为
⑸取的区间中点;
⑹计算;
⑺由于,则有零点的新区间为;
⑻取的区间中点;
⑼计算;
⑽由于,则有零点的新区间为;
⑾取的区间中点;
⑿计算;
⒀由于,则有零点的新区间为;
⒁取的区间中点
⒂计算;
⒃由于,则有零点的新区间为;
⒄取的区间中点;
⒅计算;
⒆由于,
⒇由于,则有零点的新区间为;又因为零点要求精确到,而区间两端点近似值相同都是2.24,所以函数的一个正零点为:2.24.
类型五、用二分法解决实际问题
例6.某电脑公司生产A种型号的笔记本电脑,2006年平均每台电脑生产成本5000元,并以纯利润20%标定出厂价.从2007年开始,公司更新设备,加强管理,逐步推行股份制,从而使生产成本逐年降低,2010年平均每台A种型号的笔记本电脑尽管出厂价仅是2006年出厂价的80%,但却实现了纯利润50%的高效益.
(1)求2010年每台电脑的生产成本;
(2)以2006年的生产成本为基数,用二分法求2006~2010年生产成本平均每年降低的百分率(精确到0.01)
【答案】 (1)3200;(2)11%
【解析】 (1)设2010年每台电脑的生产成本为P元,根据题意,得P(1+50%)=5000×(1+20%)×80%,解得P=3200(元).
故2010年每台电脑的生产成本为3200元.
(2)设2006~2010年生产成本平均每年降低的百分率为x,根据题意,得5000(1-x)4=3200(0<x<1),令f(x)=5000(1―x)4―3200,作出x,f (x)的对应值表:
x
0
0.1
0.15
0.2
0.3
0.45
f (x)
1800
80.5
-590
-1153
-2000
-2742
观察上表,可知f (0.1)·f (0.15)<0,说明此函数在区间(0.1,0.5)内有零点x0.取区间(0.1,0.15)的中点x1=0.125,可得f (0.125)≈-269.因为f (0.125)·f (0.1)<0,所以x0∈(0.1,0.125).再取(0.1,0.125)的中点x2=0.1125,可得f (0.1125)≈-98.因为f (0.1)·f (0.1125)<0,所以x0∈(0.1,0.1125).
同理可得,x0∈(0.1,0.10625),x0∈(0.103125,0.10625),x0∈(0.104687,0.10625),x0∈(0.10546875,0.10625),由于|0.10546875-0.10625|<0.01,所以原方程的近似解为0.11.故2006~2010生产成本平均每年降低的百分率为11%.
举一反三:
【变式1】 如右图所示,有一块边长为15 cm的正方形铁皮,将其四个角各截去一个边长为x cm的小正方形,然后折成一个无盖的盒子.
(1)求出盒子的体积y(cm3)以x(cm)为自变量的函数解析式,并讨论这个函数的定义域;
(2)如果要做成一个容积是150 cm3的无盖盒子,那么截去的小正方形的边长x是多少?(精确到0.1 cm)
【答案】(1)y=x(15-2x)2 0<x<7.5 (2)0.8 cm或4.7 cm
【解析】(1)由题意,盒子的体积y以x为自变量的函数解析式y=x(15-2x)2,其定义域为,即0<x<7.5.
(2)原问题可转化为当y=150时,求方程x(15―2x)2=150的近似解.
设g(x)=x(15―2x)2―150,由于g(0)·g(1)<0且g(4)·g(5)<0.所以方程在(0,1),(4,5)内各有一根,在区间(0,1)内的近似解为0.8,其逼近区间为(0.8125,0.875),且|0.8125-0.875|=0.0625<0.1;在区间(4,5)内的近似解为4.7,其逼近区间为(4.625,4.6875),且|4.626-4.6875|=0.0625<0.1.所以截去的小正方形的边长是0.8 cm或4.7 cm.
【巩固练习】
1.函数的零点是( ).
A.-1,4 B. -4,1 C.,1 D.,-1
2.函数的定义域是( )
A. B. C. D.
3.若方程有两个不相等的实数根,则实数的取值范围是( )
A. B. C. ,且 D. ,且
4.已知函数有唯一零点,则下列区间必存在零点的是( )
A. B. C. D.
5. 关于“二分法”求方程的近似解,说法正确的是( )
A.“二分法”求方程的近似解一定可将y=f(x)在[a,b]内的所有零点得到;
B.“二分法”求方程的近似解有可能得不到y=f(x)在[a,b]内的零点;
C.应用“二分法”求方程的近似解,y=f(x)在[a,b]内有可能无零点;
D.“二分法”求方程的近似解可能得到f(x)=0在[a,b]内的精确解.
6.若函数没有零点,则实数的取值范围是( )
A. B. C. D.
7.设函数是[-1,1]上的增函数,且,则方程在[-1,1]内( )
A.可能有3个实数根 B.可能有2个实数根 C.有唯一的实数根 D.没有实数根
8. 若函数y=f(x)在区间[a,b]上的图象为连续不断的一条曲线,则下列说法正确的是( )
A.若f(a)f(b)>0,不存在实数c∈(a,b)使得f(c)=0;
B.若f(a)f(b)<0,存在且只存在一个实数c∈(a,b),使得f(c)=0;
C.若f(a)f(b)>0,有可能存在实数c∈(a,b)使得f(c)=0;
D.若f(a)f(b)<0,有可能不存在实数c∈(a,b),使得f(c)=0.
9.函数的零点是__________.
10.若至多只有一个零点,则的取值范围是 .
11.已知抛物线的图象经过第一、二、四象限,则直线不经过第 象限.
12.三次方程在下列连续整数____________之间有根.
①-2与-1 ②-1与0 ③0与1 ④1与2 ⑤2与3
13. 已知函数的一个零点为1.
(1)求函数的其他零点;
(2)求时的取值范围.
14.用二分法求在区间的一个实根(精确到0.01).
【答案与解析】
1. 【答案】B
【解析】令,解得,故选B.
2. 【答案】D
【解析】依题意知且,解得,且.
3. 【答案】C
【解析】依题意,,,解得且.
4. 【答案】C
【解析】由题意,可知,故在上必存在零点.
故选C.
5. 【答案】D.
【解析】 由“二分法”求方程的近似解基本思想可得。
6. 【答案】B
【解析】由方程的判别式小于0,可得,故选B.
7. 【答案】C
【解析】在[-1,1]上是增函数且
在上有唯一实根
在[-1,1] 上有唯一实根.故选C.
8. 【答案】C.
【解析】由零点存在性定理知C正确.
9. 【答案】
【解析】由得,所以函数的零点是.
10.【答案】
【解析】 依题意,或综上.
11.【答案】
【解析】二 由抛物线在第一、二、四象限知,所以,即不经过第二象限.
12. 【答案】①②④
【解析】 令
x
-2
-1
0
1
2
3
f(x)
-1
1
-1
-1
7
29
在内均有根.
13.【解析】(1)依题意,设
所以解得令,即,解得.
所以函数的其他零点是.
(2)函数的三个零点将轴分成四个区间:.
作出函数的示意图如右图,观察图象得时,的取值范围是.
14.【答案】1.32
【解析】设
.
∴在内有实数解.
取为初始运算区间,用二分法逐次计算列表如下:
区间
中点
中点函数值
[1,1.5]
1.25
-0.296875
[1.25,1.5]
1.375
0.224609
[1.25,1.375]
1.3125
-0.051514
[1.3125,1.375]
1.34375
0.082611
[1.3125,1.34375]
1.328125
0.014576
[1.3125,1.328125]
1.3203125
-0.018711
[1.3203125,1.328125]
1.32421875
-0.002128
∵1.328125-1.3203125=0.0078155<0.01
∴所求根的近似值为
【学习目标】
(1)重点理解函数零点的概念,判定二次函数零点的个数,会求函数的零点;
(2)结合二次函数的图象,判断一元二次方程根的存在性及根的个数,从而了解函数零点与方程根的联系;
(3)根据具体函数的图象,能够借助计算器用二分法求函数零点的近似解,了解这种方法是求函数零点近似解的常用方法.
【经典例题】
类型一、求函数的零点
例1.已知函数.
(1)解方程(x+3)(x+1)(x―2)=0;
(2)画出函数的图象(简图),并求出函数的零点;
(3)讨论函数在零点两侧的函数值的正负.
【解析】(1)方程有三个根x1=―3,x2=―1,x3=2.
(2)函数的图象如右图,零点为―3,―1,2.
(3)由函数的图象可以直观地看出,在函数的零点―3左侧的函数值为负,在零点―3的右侧与零点―1的左侧的函数值为正,零点―1的右侧与零点2的左侧的函数值为负,零点2右侧的函数值为正.
【总结升华】(1)方程(x+3)(x+1)(x―2)=0左边是三个因式的积的形式,只要有一个因式为0,方程就成立,所以x+3=0或x+1=0或x―2=0,所以x=―3或x=―1或x=2;
(2)可以用描点的方法画出函数图象的简图;
(3)在x轴的上方,纵坐标为正,相应的函数值就为正;在x轴的下方,纵坐标为负,相应的函数值就为负.
举一反三:
【变式1】已知函数,且m,n是方程的两个根(m<n),则实数a、b、m、n的大小关系可能是( )
A.m<a<b<n B.a<m<n<b C.m<a<n<b D.a<m<b<n
【答案】 B
【解析】由函数,我们可以看到a、b为的零点,且,如右图,则应有a<m<n<b,故选B.
例2. 求下列函数的零点.
(1);
(2).
【答案】(1);(2)-1,1.
【解析】根据函数零点与方程的根之间的关系,要求函数的零点,就是求相应方程的实数根.
(1)由得,所以函数的零点是;
(2)由,令得x=1,-1,故函数的零点是-1,1.
【总结升华】求函数的零点就是求相应方程的实数根,一般可以借助求根公式或因式分解等方法,求出方程的根,从而得到函数的零点.
举一反三:
【变式1】求函数:(1);(2)的零点.
【答案】(1)-3,1;(2)-3,1,2.
【解析】(1)由求根公式解得
(2)方程可化为
由知
所以函数的零点为-3,1;函数的零点为-3,1,2.
【总结升华】三次因式分解的关键是,裂项后的两组分别要有公因式可提取,函数求零点的题目和解方程的题目可相互转化.
类型二、函数零点的存在性定理
例3.已知函数,问:方程在区间内有没有实数根?为什么?
【答案】没有实数根
【解析】先求出及的值,进而确定和的符号,当它们其中一个值小于零另一个值大于零时,便可确定在上有实数根.
,
且函数的图象是连续曲线,
在区间内有实数根
【总结升华】利用函数零点的存在性定理可以判断方程在某区间内是否有实数根,是利用计算机求方程近似根的重要依据,因此必须熟练掌握这个定理.需要注意的是,方程在区间内有实数根,不一定有.
举一反三:
【变式1】判断下列函数在给定区间上是否存在零点:
(1)
(2);
【答案】(1)存在;(2)存在;(3)存在.
【解析】(1)
故在上存在零点.
(2)
故在区间上存在零点.
【变式2】若函数,则下列判断正确的是( )
A.方程f(x)=0在区间[0,1]内一定有解
B.方程f(x)=0在区间[0,1]内一定无解
C.函数f(x)是奇函数
D.函数f(x)是偶函数
【答案】A
类型三、一元二次方程根的分布
例4. 已知关于x的二次方程x2+2mx+2m+1=0.
(1)若方程有两根,其中一根在区间(―1,0)和(1,2)内,求的取值范围.
(2)若方程两根均在区间(0,1)内,求的取值范围.
【答案】(1);(2).
【解析】 (1)条件说明函数的零点在区间(-1,0)和(1,2)内,由图1可知,
,∴.
∴.
(2)∵函数的零点在区间(0,1)内,由图2知必有.
∴.
∴.
【点评】本例两个小题均可以用解方程的方法求解,但很繁琐,而利用函数的性质和图象求解就变得非常直观简捷.“方程与函数思想”“数形结合思想”是数学中的两个重要思想,解题中要注意应用.
举一反三:
【变式1】 关于x的方程ax2―2(a+1)x+a―1=0,求a为何值时:
(1)方程有一根;
(2)方程有一正一负根;
(3)方程两根都大于1;
(4)方程有一根大于1,一根小于1.
【答案】(1)或(2)(3)不存在实数(4)
【解析】(1)当a=0时,方程变为―2x―1=0,即,符合题意;
当时,方程为二次方程,因为方程有一根,所以,解得.综上可知,当或时,关于的方程ax2―2(a+1)x+a―1=0有一根.
(2)因为方程有一正一负根,所以由根与系数的关系得.又解得.
(3)方程两根都大于1,图象大致如图
所以必须满足
或两不等式组均无解.
所以不存在实数,使方程两根都大于1.
(4)因为方程有一根大于1,一根小于1,图象大致如图
所以必须满足或解得.
类型四、用二分法求函数的零点的近似值
例5.求函数的一个正数零点(精确到0.1).
【答案】1.7
【解析】由于,可取区间作为计算的初始区间,用二分法逐步计算,列表如下:
区间
中点
中点函数值
[1,2]
1.5
-2.625
[1.5,2]
1.75
0.2344
[1.5,1.75]
1.625
-1.3027
[1.625,1.75]
1.6875
-0.5618
[1.6875,1.75]
1.71875
-0.1709
由上表计算可知,区间[1.6875,1.75]的长度1.75-1.6875=0.0625<0.1,所以可以将1.6875的近似值1.7作为函数零点的近似值.
【总结升华】应首先判断x的取正整数时,函数值的正负,使正整数所对应的区间尽量小,便于利用二分法求其近似值.
举一反三:
【变式1】若函数的一个正数零点附近的函数值
用二分法计算,其参考数据如下:
f(1)=-2
f(1.5)=0.625
f(1.25)=-0.984
f(1.375)=-0.260
f(1.4375)=0. 162
f(1.40625)=-0. 054
那么方程的一个近似根(精确到0.1)为( )
A.1.2 B.1.3 C.1.4 D.1.5
【答案】C
【变式2】用二分法求函数的一个正零点(精确到)
【答案】2.24
【解析】⑴由,可知函数的一个正零点在区间中;
⑵取的区间中点;
⑶计算;
⑷由于,则有零点的新区间为
⑸取的区间中点;
⑹计算;
⑺由于,则有零点的新区间为;
⑻取的区间中点;
⑼计算;
⑽由于,则有零点的新区间为;
⑾取的区间中点;
⑿计算;
⒀由于,则有零点的新区间为;
⒁取的区间中点
⒂计算;
⒃由于,则有零点的新区间为;
⒄取的区间中点;
⒅计算;
⒆由于,
⒇由于,则有零点的新区间为;又因为零点要求精确到,而区间两端点近似值相同都是2.24,所以函数的一个正零点为:2.24.
类型五、用二分法解决实际问题
例6.某电脑公司生产A种型号的笔记本电脑,2006年平均每台电脑生产成本5000元,并以纯利润20%标定出厂价.从2007年开始,公司更新设备,加强管理,逐步推行股份制,从而使生产成本逐年降低,2010年平均每台A种型号的笔记本电脑尽管出厂价仅是2006年出厂价的80%,但却实现了纯利润50%的高效益.
(1)求2010年每台电脑的生产成本;
(2)以2006年的生产成本为基数,用二分法求2006~2010年生产成本平均每年降低的百分率(精确到0.01)
【答案】 (1)3200;(2)11%
【解析】 (1)设2010年每台电脑的生产成本为P元,根据题意,得P(1+50%)=5000×(1+20%)×80%,解得P=3200(元).
故2010年每台电脑的生产成本为3200元.
(2)设2006~2010年生产成本平均每年降低的百分率为x,根据题意,得5000(1-x)4=3200(0<x<1),令f(x)=5000(1―x)4―3200,作出x,f (x)的对应值表:
x
0
0.1
0.15
0.2
0.3
0.45
f (x)
1800
80.5
-590
-1153
-2000
-2742
观察上表,可知f (0.1)·f (0.15)<0,说明此函数在区间(0.1,0.5)内有零点x0.取区间(0.1,0.15)的中点x1=0.125,可得f (0.125)≈-269.因为f (0.125)·f (0.1)<0,所以x0∈(0.1,0.125).再取(0.1,0.125)的中点x2=0.1125,可得f (0.1125)≈-98.因为f (0.1)·f (0.1125)<0,所以x0∈(0.1,0.1125).
同理可得,x0∈(0.1,0.10625),x0∈(0.103125,0.10625),x0∈(0.104687,0.10625),x0∈(0.10546875,0.10625),由于|0.10546875-0.10625|<0.01,所以原方程的近似解为0.11.故2006~2010生产成本平均每年降低的百分率为11%.
举一反三:
【变式1】 如右图所示,有一块边长为15 cm的正方形铁皮,将其四个角各截去一个边长为x cm的小正方形,然后折成一个无盖的盒子.
(1)求出盒子的体积y(cm3)以x(cm)为自变量的函数解析式,并讨论这个函数的定义域;
(2)如果要做成一个容积是150 cm3的无盖盒子,那么截去的小正方形的边长x是多少?(精确到0.1 cm)
【答案】(1)y=x(15-2x)2 0<x<7.5 (2)0.8 cm或4.7 cm
【解析】(1)由题意,盒子的体积y以x为自变量的函数解析式y=x(15-2x)2,其定义域为,即0<x<7.5.
(2)原问题可转化为当y=150时,求方程x(15―2x)2=150的近似解.
设g(x)=x(15―2x)2―150,由于g(0)·g(1)<0且g(4)·g(5)<0.所以方程在(0,1),(4,5)内各有一根,在区间(0,1)内的近似解为0.8,其逼近区间为(0.8125,0.875),且|0.8125-0.875|=0.0625<0.1;在区间(4,5)内的近似解为4.7,其逼近区间为(4.625,4.6875),且|4.626-4.6875|=0.0625<0.1.所以截去的小正方形的边长是0.8 cm或4.7 cm.
【巩固练习】
1.函数的零点是( ).
A.-1,4 B. -4,1 C.,1 D.,-1
2.函数的定义域是( )
A. B. C. D.
3.若方程有两个不相等的实数根,则实数的取值范围是( )
A. B. C. ,且 D. ,且
4.已知函数有唯一零点,则下列区间必存在零点的是( )
A. B. C. D.
5. 关于“二分法”求方程的近似解,说法正确的是( )
A.“二分法”求方程的近似解一定可将y=f(x)在[a,b]内的所有零点得到;
B.“二分法”求方程的近似解有可能得不到y=f(x)在[a,b]内的零点;
C.应用“二分法”求方程的近似解,y=f(x)在[a,b]内有可能无零点;
D.“二分法”求方程的近似解可能得到f(x)=0在[a,b]内的精确解.
6.若函数没有零点,则实数的取值范围是( )
A. B. C. D.
7.设函数是[-1,1]上的增函数,且,则方程在[-1,1]内( )
A.可能有3个实数根 B.可能有2个实数根 C.有唯一的实数根 D.没有实数根
8. 若函数y=f(x)在区间[a,b]上的图象为连续不断的一条曲线,则下列说法正确的是( )
A.若f(a)f(b)>0,不存在实数c∈(a,b)使得f(c)=0;
B.若f(a)f(b)<0,存在且只存在一个实数c∈(a,b),使得f(c)=0;
C.若f(a)f(b)>0,有可能存在实数c∈(a,b)使得f(c)=0;
D.若f(a)f(b)<0,有可能不存在实数c∈(a,b),使得f(c)=0.
9.函数的零点是__________.
10.若至多只有一个零点,则的取值范围是 .
11.已知抛物线的图象经过第一、二、四象限,则直线不经过第 象限.
12.三次方程在下列连续整数____________之间有根.
①-2与-1 ②-1与0 ③0与1 ④1与2 ⑤2与3
13. 已知函数的一个零点为1.
(1)求函数的其他零点;
(2)求时的取值范围.
14.用二分法求在区间的一个实根(精确到0.01).
【答案与解析】
1. 【答案】B
【解析】令,解得,故选B.
2. 【答案】D
【解析】依题意知且,解得,且.
3. 【答案】C
【解析】依题意,,,解得且.
4. 【答案】C
【解析】由题意,可知,故在上必存在零点.
故选C.
5. 【答案】D.
【解析】 由“二分法”求方程的近似解基本思想可得。
6. 【答案】B
【解析】由方程的判别式小于0,可得,故选B.
7. 【答案】C
【解析】在[-1,1]上是增函数且
在上有唯一实根
在[-1,1] 上有唯一实根.故选C.
8. 【答案】C.
【解析】由零点存在性定理知C正确.
9. 【答案】
【解析】由得,所以函数的零点是.
10.【答案】
【解析】 依题意,或综上.
11.【答案】
【解析】二 由抛物线在第一、二、四象限知,所以,即不经过第二象限.
12. 【答案】①②④
【解析】 令
x
-2
-1
0
1
2
3
f(x)
-1
1
-1
-1
7
29
在内均有根.
13.【解析】(1)依题意,设
所以解得令,即,解得.
所以函数的其他零点是.
(2)函数的三个零点将轴分成四个区间:.
作出函数的示意图如右图,观察图象得时,的取值范围是.
14.【答案】1.32
【解析】设
.
∴在内有实数解.
取为初始运算区间,用二分法逐次计算列表如下:
区间
中点
中点函数值
[1,1.5]
1.25
-0.296875
[1.25,1.5]
1.375
0.224609
[1.25,1.375]
1.3125
-0.051514
[1.3125,1.375]
1.34375
0.082611
[1.3125,1.34375]
1.328125
0.014576
[1.3125,1.328125]
1.3203125
-0.018711
[1.3203125,1.328125]
1.32421875
-0.002128
∵1.328125-1.3203125=0.0078155<0.01
∴所求根的近似值为
