五年级下册数学课件-一简易方程第7课时苏教版 (共19张PPT)
文档属性
| 名称 | 五年级下册数学课件-一简易方程第7课时苏教版 (共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1015.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-03 15:17:19 | ||
图片预览






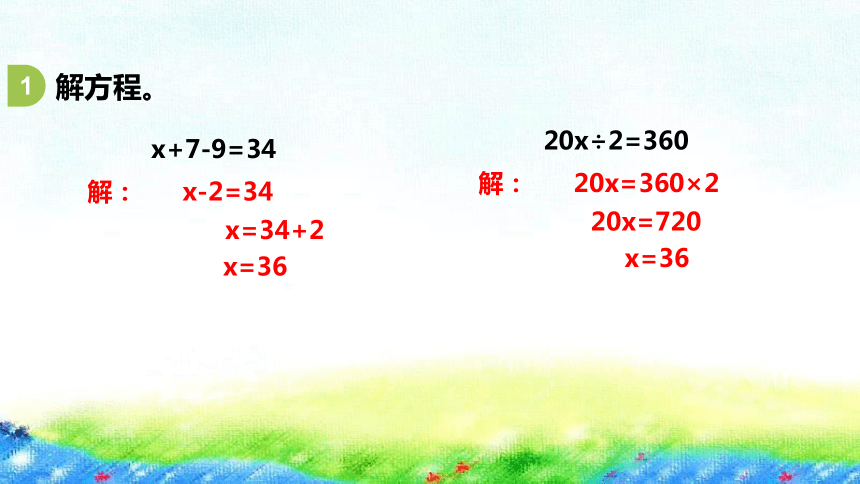
文档简介
(共19张PPT)
简易方程
第 7 课时 解方程和列方程解决简单实际问题练习
苏教版 数学 五年级 下册
1.进一步理解并掌握形如ax±b=c和ax÷b=c的方程的解法,能找出实际问题里数量之间的相等关系,列方程解决两步计算的实际问题。
2.通过观察、分析、抽象、概括和交流等数学活动,经历将显示问题抽象为方程的过程,进一步培养分析推理、抽象概括等思维能力,进一步体会方程思想,提高解决问题的能力。
【重点】列方程解决两步计算的实际问题和解方程。
【难点】分析和找准实际问题里的等量关系。
回忆一下,我们在简易方程这个单元里,已经学习了哪些知识?
1
找出下面语句中数量之间的相等关系。
(1)上衣单价比裤子贵46元。
(2)母鸡有42只,是公鸡的3.5倍。
上衣的元数 - 裤子的元数 = 46元
公鸡的只数 × 3.5 = 42只
1
找出下面语句中数量之间的相等关系。
(3)5瓶饮料共6.25升。
(4)油库有一批汽油,运走25吨,还剩98吨。
每瓶饮料的升数 × 瓶数 = 6.25升
一批汽油的总吨数 - 运走的吨数 = 还剩的吨数
1
找出下面语句中数量之间的相等关系。
(5)月季花的盆数比海棠花的2倍少12盆。
(6)小树林的面积400平方米,比草坪的3倍多2.5平方米。
海棠花的盆数 × 2 -12盆 = 月季花的盆数
草坪的面积 × 3 + 2.5平方米 = 小树林的面积
1
解方程。
x+7-9=34
解: x-2=34
x=34+2
x=36
20x÷2=360
解: 20x=360×2
20x=720
x=36
1
解方程。
2.3x-1.02=0.36
解: 2.3x=0.36+1.02
2.3x=1.38
x=0.6
4+2.5x=20
解: 2.5x=20-4
2.5x=16
x=6.4
1
解方程。
4x-4.8=5.6
解: 4x=5.6+4.8
4x=10.4
x=2.6
13x+65=169
解: 13x=169-65
13x=104
x=8
2
求x的值。
1.3x÷2=0.39
解: 1.3x=0.39×2
1.3x=0.78
x=0.6
2
求x的值。
3x+1.8=19.8
解: 3x=19.8-18
3x=1.8
x=0.6
3
小明原来有一些邮票,今年又收集了24枚,送给小军30枚后,还剩52枚。小明原来有邮票多少枚?
x+24-30=52
解:设小明原来有邮票x枚。
x=52-24+30
x=58
答:小明原来有邮票58枚。
1
一种饮料有两种规格的包装。大瓶容量1.5升,是小瓶容量的3倍。小瓶的单价是1.8元/瓶,比大瓶便宜3.2元/瓶。求小瓶的容量和大瓶的单价。
3x=1.5
解:设小瓶的容量是x升。
x=1.5÷3
x=0.5
答:小瓶的容量是0.5升。
1
一种饮料有两种规格的包装。大瓶容量1.5升,是小瓶容量的3倍。小瓶的单价是1.8元/瓶,比大瓶便宜3.2元/瓶。求小瓶的容量和大瓶的单价。
y-3.2=1.8
解:设大瓶的单价是y元/瓶。
y=1.8+3.2
y=5
答:大瓶的单价是5元/瓶。
1
小亮现在身高1.53米,体重46.5千克。他现在的身高比出生时的3倍少0.03米,体重比出生时的14倍多1.7千克。小亮出生时的身高和体重各是多少?
3x-0.03=1.53
解:设小亮出生时的身高x米。
3x=1.53+0.03
3x=1.56
答:小亮出生时的身高是0.52米。
x=0.52
1.检验方程的解是否正确,只要把方程的解代入原方程,看左边和右边是不是相等。
2.有时顺着条件里数量变化情况直接列方程,解方程求出结果,比反过来思考方便得多。
3.有时可以根据计算公式列方程解决问题。遇到这样的问题,通常只要按照公式列出方程,再解方程求出结果。
1
小亮现在身高1.53米,体重46.5千克。他现在的身高比出生时的3倍少0.03米,体重比出生时的14倍多1.7千克。小亮出生时的身高和体重各是多少?
14y+1.7=46.5
解:设小亮出生时的体重是y千克。
14y=46.5-1.7
14y=44.8
答:小亮出生时的体重是3.2千克。
y=3.2
2
每瓶墨水多少元?
12x+3.5=25.1
解:设每瓶墨水x元。
12x=25.1-3.5
12x=21.6
答:每瓶墨水1.8元。
x=1.8
3
我国测量温度常用℃(摄氏度)作单位,有时还使用℉(华氏度)作单位。华氏温度和摄氏温度可以用下面的公式进行换算:
华氏温度=摄氏温度×1.8+32
下图温度计上表示的温度是86℉,相当于多少℃?
1.8x+32=86
解:设温度86℉相当于x℃。
1.8x=86-32
1.8x=54
答:温度86℉相当于30℃。
x=30
简易方程
第 7 课时 解方程和列方程解决简单实际问题练习
苏教版 数学 五年级 下册
1.进一步理解并掌握形如ax±b=c和ax÷b=c的方程的解法,能找出实际问题里数量之间的相等关系,列方程解决两步计算的实际问题。
2.通过观察、分析、抽象、概括和交流等数学活动,经历将显示问题抽象为方程的过程,进一步培养分析推理、抽象概括等思维能力,进一步体会方程思想,提高解决问题的能力。
【重点】列方程解决两步计算的实际问题和解方程。
【难点】分析和找准实际问题里的等量关系。
回忆一下,我们在简易方程这个单元里,已经学习了哪些知识?
1
找出下面语句中数量之间的相等关系。
(1)上衣单价比裤子贵46元。
(2)母鸡有42只,是公鸡的3.5倍。
上衣的元数 - 裤子的元数 = 46元
公鸡的只数 × 3.5 = 42只
1
找出下面语句中数量之间的相等关系。
(3)5瓶饮料共6.25升。
(4)油库有一批汽油,运走25吨,还剩98吨。
每瓶饮料的升数 × 瓶数 = 6.25升
一批汽油的总吨数 - 运走的吨数 = 还剩的吨数
1
找出下面语句中数量之间的相等关系。
(5)月季花的盆数比海棠花的2倍少12盆。
(6)小树林的面积400平方米,比草坪的3倍多2.5平方米。
海棠花的盆数 × 2 -12盆 = 月季花的盆数
草坪的面积 × 3 + 2.5平方米 = 小树林的面积
1
解方程。
x+7-9=34
解: x-2=34
x=34+2
x=36
20x÷2=360
解: 20x=360×2
20x=720
x=36
1
解方程。
2.3x-1.02=0.36
解: 2.3x=0.36+1.02
2.3x=1.38
x=0.6
4+2.5x=20
解: 2.5x=20-4
2.5x=16
x=6.4
1
解方程。
4x-4.8=5.6
解: 4x=5.6+4.8
4x=10.4
x=2.6
13x+65=169
解: 13x=169-65
13x=104
x=8
2
求x的值。
1.3x÷2=0.39
解: 1.3x=0.39×2
1.3x=0.78
x=0.6
2
求x的值。
3x+1.8=19.8
解: 3x=19.8-18
3x=1.8
x=0.6
3
小明原来有一些邮票,今年又收集了24枚,送给小军30枚后,还剩52枚。小明原来有邮票多少枚?
x+24-30=52
解:设小明原来有邮票x枚。
x=52-24+30
x=58
答:小明原来有邮票58枚。
1
一种饮料有两种规格的包装。大瓶容量1.5升,是小瓶容量的3倍。小瓶的单价是1.8元/瓶,比大瓶便宜3.2元/瓶。求小瓶的容量和大瓶的单价。
3x=1.5
解:设小瓶的容量是x升。
x=1.5÷3
x=0.5
答:小瓶的容量是0.5升。
1
一种饮料有两种规格的包装。大瓶容量1.5升,是小瓶容量的3倍。小瓶的单价是1.8元/瓶,比大瓶便宜3.2元/瓶。求小瓶的容量和大瓶的单价。
y-3.2=1.8
解:设大瓶的单价是y元/瓶。
y=1.8+3.2
y=5
答:大瓶的单价是5元/瓶。
1
小亮现在身高1.53米,体重46.5千克。他现在的身高比出生时的3倍少0.03米,体重比出生时的14倍多1.7千克。小亮出生时的身高和体重各是多少?
3x-0.03=1.53
解:设小亮出生时的身高x米。
3x=1.53+0.03
3x=1.56
答:小亮出生时的身高是0.52米。
x=0.52
1.检验方程的解是否正确,只要把方程的解代入原方程,看左边和右边是不是相等。
2.有时顺着条件里数量变化情况直接列方程,解方程求出结果,比反过来思考方便得多。
3.有时可以根据计算公式列方程解决问题。遇到这样的问题,通常只要按照公式列出方程,再解方程求出结果。
1
小亮现在身高1.53米,体重46.5千克。他现在的身高比出生时的3倍少0.03米,体重比出生时的14倍多1.7千克。小亮出生时的身高和体重各是多少?
14y+1.7=46.5
解:设小亮出生时的体重是y千克。
14y=46.5-1.7
14y=44.8
答:小亮出生时的体重是3.2千克。
y=3.2
2
每瓶墨水多少元?
12x+3.5=25.1
解:设每瓶墨水x元。
12x=25.1-3.5
12x=21.6
答:每瓶墨水1.8元。
x=1.8
3
我国测量温度常用℃(摄氏度)作单位,有时还使用℉(华氏度)作单位。华氏温度和摄氏温度可以用下面的公式进行换算:
华氏温度=摄氏温度×1.8+32
下图温度计上表示的温度是86℉,相当于多少℃?
1.8x+32=86
解:设温度86℉相当于x℃。
1.8x=86-32
1.8x=54
答:温度86℉相当于30℃。
x=30
