六年级下册数学试题-第四单元圆柱和圆锥单元测试二(含答案) 冀教版
文档属性
| 名称 | 六年级下册数学试题-第四单元圆柱和圆锥单元测试二(含答案) 冀教版 |  | |
| 格式 | zip | ||
| 文件大小 | 375.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-03 19:06:45 | ||
图片预览

文档简介
第四单元圆柱和圆锥测试题
一、填空。
(1)一个圆锥的体积是16.5立方分米,和它等底等高的圆柱的体积是( )立方分米。
(2)把一个长8厘米、宽6厘米的长方形纸板分成两个相等的直角三角形(如图)。然后以直角三角形较长的直角边所在的直线为轴,将纸板旋转一周,可以得到一个( )体,它的体积是( )立方厘米(π=3.14)。
(3)把一个圆柱形木块削成一个最大的圆锥,削去部分的体积是25.12立方厘米。原来圆柱形木块的体积是( )立方厘米,削成的圆锥形木块的体积是( )立方厘米。
(4)右图中瓶底的面积与杯口的面积相等,将瓶子中的
液体全部倒入杯子中,最多能够倒满( )杯。
(5)一个圆柱和一个圆锥,它们的底面半径相等,圆柱的高是圆锥的 。如果圆锥的体积
是6立方米,圆柱的体积是( )立方米。
(6)把300厘米长的圆柱形钢材截成2段(每段还是圆柱体),表面积增加了18平方厘米,这段钢材原来体积是( )立方厘米。
(7)一个圆柱和一个圆锥等底等高,如果它们的体积相差32立方分米,那么圆锥的体积为(????? )立方分米。
(8)用右图中的阴影部分恰好可以制作一个圆柱,这个圆柱的底面周长是( )厘米,底面直径是( )厘米,高是( )厘米,表面积是( )平方厘米,体积是( )立方厘米。
二、选择,将正确答案的序号填入括号内。
(1)如果一个圆柱体的底面半径和高都扩大3倍,那么它的体积扩大( )倍。
①3 ②6 ③9 ④27
(2)甲、乙两人都用一张长50厘米、宽25厘米的纸,用两种不同的方法围成一个圆柱(接头处不重叠),那么围成的圆柱( )。
①侧面积一定相等 ②高一定相等
③侧面积和高都相等 ④侧面积和高都不相等
(3)用一个高60厘米的圆锥形容器盛满水,倒入和它等底的圆柱形容器中,水的高度是( )厘米。
①60 ②40 ③30 ④20
(4)把一个圆柱体的木块沿底面直径从上到下切成两半,这个切面正好是一个正方形。已知正方形的面积是36平方厘米,那么其中一个半圆柱体的体积是( )立方厘米。
①27π ②36π ③54π ④216π
三、解决问题。
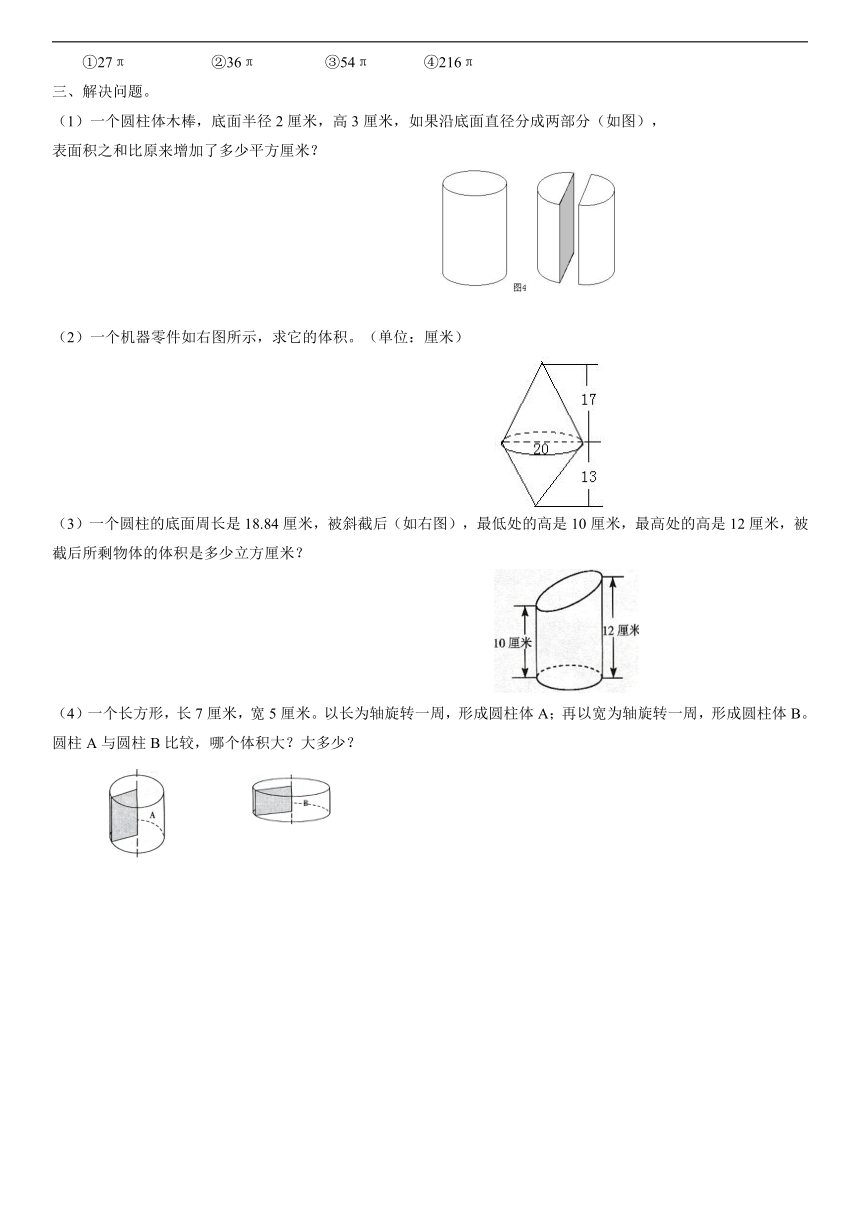
(1)一个圆柱体木棒,底面半径2厘米,高3厘米,如果沿底面直径分成两部分(如图),
表面积之和比原来增加了多少平方厘米?
(2)一个机器零件如右图所示,求它的体积。(单位:厘米)
(3)一个圆柱的底面周长是18.84厘米,被斜截后(如右图),最低处的高是10厘米,最高处的高是12厘米,被截后所剩物体的体积是多少立方厘米?
(4)一个长方形,长7厘米,宽5厘米。以长为轴旋转一周,形成圆柱体A;再以宽为轴旋转一周,形成圆柱体B。圆柱A与圆柱B比较,哪个体积大?大多少?
答案
一、填空。
(1)一个圆锥的体积是16.5立方分米,和它等底等高的圆柱的体积是( 49.5 )立方分米。
(2)把一个长8厘米、宽6厘米的长方形纸板分成两个相等的直角三角形(如图)。然后以直角三角形较长的直角边所在的直线为轴,将纸板旋转一周,可以得到一个(圆锥)体,它的体积是(301.44)立方厘米(π=3.14)。
(3)把一个圆柱形木块削成一个最大的圆锥,削去部分的体积是25.12立方厘米。原来圆柱形木块的体积是(37.68 )立方厘米,削成的圆锥形木块的体积是( 12.56 )立方厘米。
(4)右图中瓶底的面积与杯口的面积相等,将瓶子中的
液体全部倒入杯子中,最多能够倒满( 6)杯。
(5)一个圆柱和一个圆锥,它们的底面半径相等,圆柱的高是圆锥的 。如果圆锥的体积
是6立方米,圆柱的体积是(6)立方米。
(6)把300厘米长的圆柱形钢材截成2段(每段还是圆柱体),表面积增加了18平方厘米,这段钢材原来体积是(2700)立方厘米。
(7)一个圆柱和一个圆锥等底等高,如果它们的体积相差32立方分米,那么圆锥的体积为(4)立方分米。
(8)用右图中的阴影部分恰好可以制作一个圆柱,这个圆柱的 底面周长是( 31.4 )厘米,底面直径是( 10 )厘米,高是( 20 )厘米,表面积是(785 )平方厘米,体积是(1570 )立方厘米。
二、选择,将正确答案的序号填入括号内。
(1)如果一个圆柱体的底面半径和高都扩大3倍,那么它的体积扩大( ④ )倍。
①3 ②6 ③9 ④27
(2)甲、乙两人都用一张长50厘米、宽25厘米的纸,用两种不同的方法围成一个圆柱(接头处不重叠),那么围成的圆柱( ① )。
①侧面积一定相等 ②高一定相等
③侧面积和高都相等 ④侧面积和高都不相等
(3)用一个高60厘米的圆锥形容器盛满水,倒入和它等底的圆柱形容器中,水的高度是( ④ )厘米。
①60 ②40 ③30 ④20
(4)把一个圆柱体的木块沿底面直径从上到下切成两半,这个切面正好是一个正方形。已知正方形的面积是36平方厘米,那么其中一个半圆柱体的体积是( ① )立方厘米。
①27π ②36π ③54π ④216π
三、解决问题。
(1)一个圆柱体木棒,底面半径2厘米,高3厘米,如果沿底面直径分成两部分(如图),
表面积之和比原来增加了多少平方厘米?
2×2×3×2=24(平方厘米)
(2)一个机器零件如右图所示,求它的体积(单位:厘米)
半径:20÷2=10(厘米)
体积:10×10×3.14×(17+13)÷3=3140(立方厘米)
(3)一个圆柱的底面周长是18.84厘米,被斜截后(如右图),最低处的高是10厘米,最高处的高是12厘米,被截后所剩物体的体积是多少立方厘米?
半径:18.84÷3.14÷2=3(厘米)
所剩体积:3×3×3.14×(10+12)÷2=56.52(立方厘米)
(4)一个长方形,长7厘米,宽5厘米。以长为轴旋转一周,形成圆柱体A;再以宽为轴旋转一周,形成圆柱体B。圆柱A与圆柱B比较,哪个体积大?大多少?
A:5×5×3.14×7
B:7×7×3.14×5
B>A
