四年级下册数学课件-5.5 解方程(二)-北师大版(共19张PPT)
文档属性
| 名称 | 四年级下册数学课件-5.5 解方程(二)-北师大版(共19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-03 00:00:00 | ||
图片预览




文档简介
(共19张PPT)
5.5 解方程(二)
五 认识方程
学习目标
通过观察天平称重的具体情境,类比等式变形的过程,抽象出等式性质,即等式两边都乘同一个数(或除以同一个不为0的数),等式仍然成立;进一步了解等式性质是解方程的根据。
会用等式的性质解形如2x=10的简单方程。
回顾复习
解方程。
7.8+x=10.6 x-12.8=9.2
x-4.3=2.1 5.6+x=8.9
解:7.8+x-7.8=10.6-7.8
x=2.8
解:x-12.8+12.8=9.2+12.8
x=22
解:x-4.3+4.3=2.1+4.3
x=6.4
解:5.6+x-5.6=8.9-5.6
x=3.3
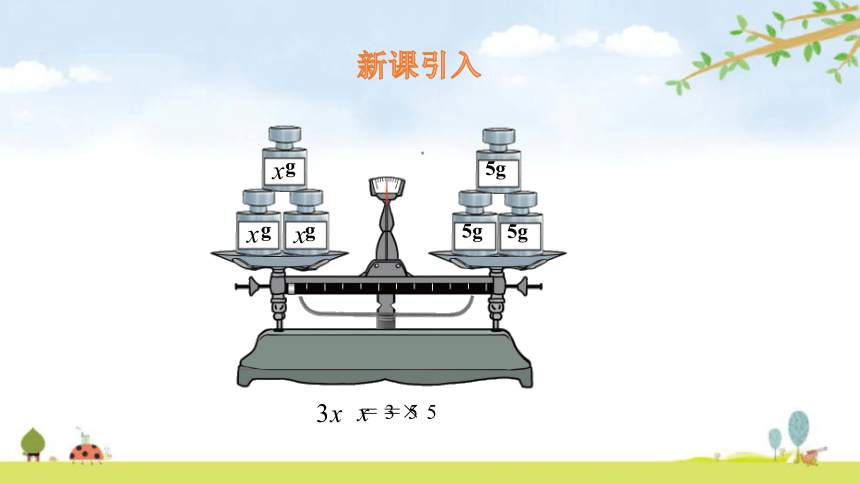
新课引入
5g
g
=5
5g
g
5g
g
=3×5
新课引入
10g
10g
=20
g
÷2=20÷2
g
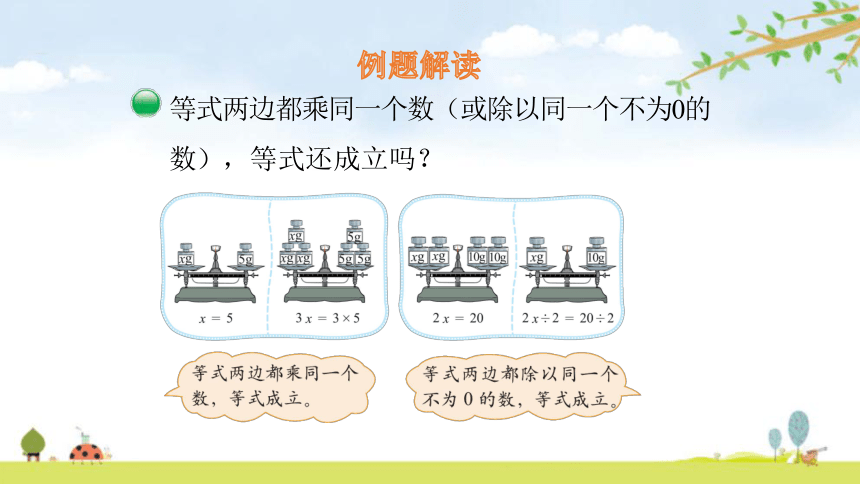
例题解读
等式两边都乘同一个数(或除以同一个不为0的数),等式还成立吗?
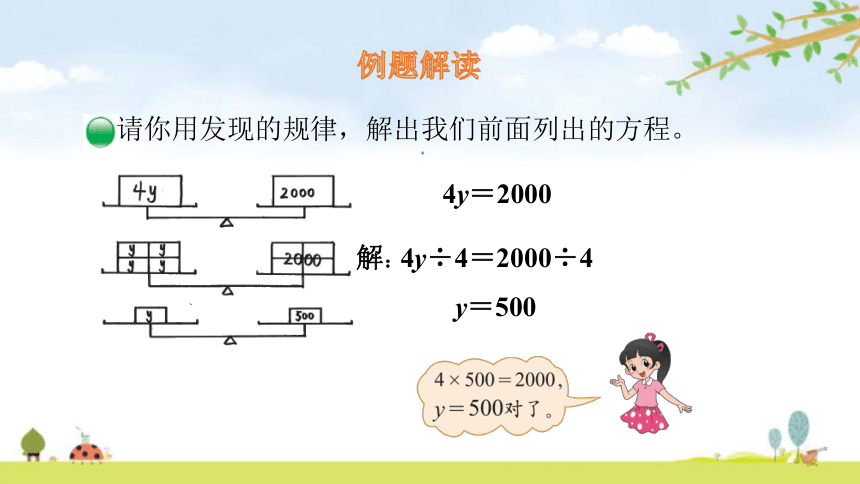
例题解读
4y=2000
解:
4y÷4=2000÷4
y=500
请你用发现的规律,解出我们前面列出的方程。
例题解读
解方程。
7y=28
解:
7y÷7=28÷7
y=4
x÷3 =9
解:
x÷3×3=9×3
x=27
27÷3=9,x=27对了。
7×4=28, y=4对了。
例题解读
下面解法正确吗?与同伴交流。
38
小结
等式的性质2
等式的两边都乘同一个数(或除以同一个不为0的数),等式仍然成立。
利用等式的性质2解形如ax=b和x÷a=b的方程
解形如ax=b和x÷a=b的方程可根据等式的性质2,在方程的两边同时除以a(a≠0)或乘a,使方程左边只剩下未知数x,这时方程右边的数b÷a或ab就是x的值。
随堂小测
1.森林医生。
=35=35÷7=5
-5=8
解:
-5 =8
=3
-5
-5
+5
+5
=13
=35
解:
÷7=35÷7
=5
随堂小测
2.解方程。
6x=156
x=26
6x÷6=156÷6
解:
3x=630
x=210
3x÷3=630÷3
解:
随堂小测
x-47=47
x=94
x-47+47=47+47
解:
59+x=120
x=61
59+x-59=120-59
解:
x÷52=7
x=364
x÷52×52=7×52
解:
x=0
解:
x÷28=0
x÷28×28=0×28
随堂小测
3.
⑴这个正方形花坛的边长是多少米?列方程并解答。
解:设这个正方形花坛的边长是x米。
4x=24
x=6
4x÷4=24÷4
答:这个正方形花坛的边长是6米。
随堂小测
⑵如果把这个花坛改为长方形,周长
不变,长是多少米?列方程并解答。
解:设长为x米。
(x+4)×2 = 24
x+4 = 24÷2
答:长是8米。
x+4-4 = 12-4
x = 8
2.
随堂小测
4.某地为便于残疾人轮椅通行,通过了一项关于建筑物前斜坡高度的规定:每1米高的斜坡,至少需要12米的水平长度。
⑴2米高的斜坡,至少需要多少米的水平长度?
4米、x米高呢?
⑵某建筑物前的空地长36米,
那么此处斜坡最高多少米?
随堂小测
⑴2米高的斜坡,至少需要多少米的水平长度?
4米、x米高呢?
12×2=24(米)
12×4=48(米)
12x米
2米高:
4米高:
x米高:
随堂小测
⑵某建筑物前的空地长36米,那么此处斜坡最高多少米?
解:设此处斜坡最高x米。
12x=36
12x÷12=36÷12
x=3
答:此处斜坡最高3米。
课后作业
1.从课后习题中选取。
5.5 解方程(二)
五 认识方程
学习目标
通过观察天平称重的具体情境,类比等式变形的过程,抽象出等式性质,即等式两边都乘同一个数(或除以同一个不为0的数),等式仍然成立;进一步了解等式性质是解方程的根据。
会用等式的性质解形如2x=10的简单方程。
回顾复习
解方程。
7.8+x=10.6 x-12.8=9.2
x-4.3=2.1 5.6+x=8.9
解:7.8+x-7.8=10.6-7.8
x=2.8
解:x-12.8+12.8=9.2+12.8
x=22
解:x-4.3+4.3=2.1+4.3
x=6.4
解:5.6+x-5.6=8.9-5.6
x=3.3
新课引入
5g
g
=5
5g
g
5g
g
=3×5
新课引入
10g
10g
=20
g
÷2=20÷2
g
例题解读
等式两边都乘同一个数(或除以同一个不为0的数),等式还成立吗?
例题解读
4y=2000
解:
4y÷4=2000÷4
y=500
请你用发现的规律,解出我们前面列出的方程。
例题解读
解方程。
7y=28
解:
7y÷7=28÷7
y=4
x÷3 =9
解:
x÷3×3=9×3
x=27
27÷3=9,x=27对了。
7×4=28, y=4对了。
例题解读
下面解法正确吗?与同伴交流。
38
小结
等式的性质2
等式的两边都乘同一个数(或除以同一个不为0的数),等式仍然成立。
利用等式的性质2解形如ax=b和x÷a=b的方程
解形如ax=b和x÷a=b的方程可根据等式的性质2,在方程的两边同时除以a(a≠0)或乘a,使方程左边只剩下未知数x,这时方程右边的数b÷a或ab就是x的值。
随堂小测
1.森林医生。
=35=35÷7=5
-5=8
解:
-5 =8
=3
-5
-5
+5
+5
=13
=35
解:
÷7=35÷7
=5
随堂小测
2.解方程。
6x=156
x=26
6x÷6=156÷6
解:
3x=630
x=210
3x÷3=630÷3
解:
随堂小测
x-47=47
x=94
x-47+47=47+47
解:
59+x=120
x=61
59+x-59=120-59
解:
x÷52=7
x=364
x÷52×52=7×52
解:
x=0
解:
x÷28=0
x÷28×28=0×28
随堂小测
3.
⑴这个正方形花坛的边长是多少米?列方程并解答。
解:设这个正方形花坛的边长是x米。
4x=24
x=6
4x÷4=24÷4
答:这个正方形花坛的边长是6米。
随堂小测
⑵如果把这个花坛改为长方形,周长
不变,长是多少米?列方程并解答。
解:设长为x米。
(x+4)×2 = 24
x+4 = 24÷2
答:长是8米。
x+4-4 = 12-4
x = 8
2.
随堂小测
4.某地为便于残疾人轮椅通行,通过了一项关于建筑物前斜坡高度的规定:每1米高的斜坡,至少需要12米的水平长度。
⑴2米高的斜坡,至少需要多少米的水平长度?
4米、x米高呢?
⑵某建筑物前的空地长36米,
那么此处斜坡最高多少米?
随堂小测
⑴2米高的斜坡,至少需要多少米的水平长度?
4米、x米高呢?
12×2=24(米)
12×4=48(米)
12x米
2米高:
4米高:
x米高:
随堂小测
⑵某建筑物前的空地长36米,那么此处斜坡最高多少米?
解:设此处斜坡最高x米。
12x=36
12x÷12=36÷12
x=3
答:此处斜坡最高3米。
课后作业
1.从课后习题中选取。
