四年级下册数学课件-密铺-北师大版(共19张PPT)
文档属性
| 名称 | 四年级下册数学课件-密铺-北师大版(共19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-03 00:00:00 | ||
图片预览




文档简介
(共19张PPT)
密 铺
数学好玩
学习目标
经历探索平面图形密铺的活动,复习学过的图形知识,初步了解一些平面图形可以密铺的道理。
能进行简单的密铺设计,积累相关活动经验,培养初步的空间观念,提高解决问题的能力。
结合密铺活动感受数学在生活中的广泛应用,发展学生对数学学习的兴趣,结合自我评价发展学生反思能力。
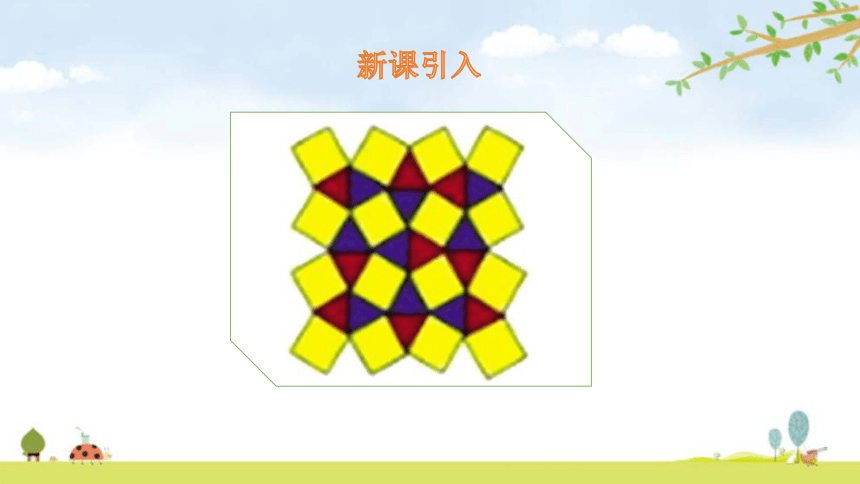
新课引入
新课引入
例题解读
活动任务
三角形能不能密铺?四边形可不可以?
例题解读
设计方案
解决这个问题需要哪些主要步骤?
你想采取怎样的方式解决问题?(独立完成/小组合)如果是小组合作,怎样进行分工?
把主要步骤、分工写下来。
图形的
选择
图形的
准备
小组的
分工
呈现的
方式
……
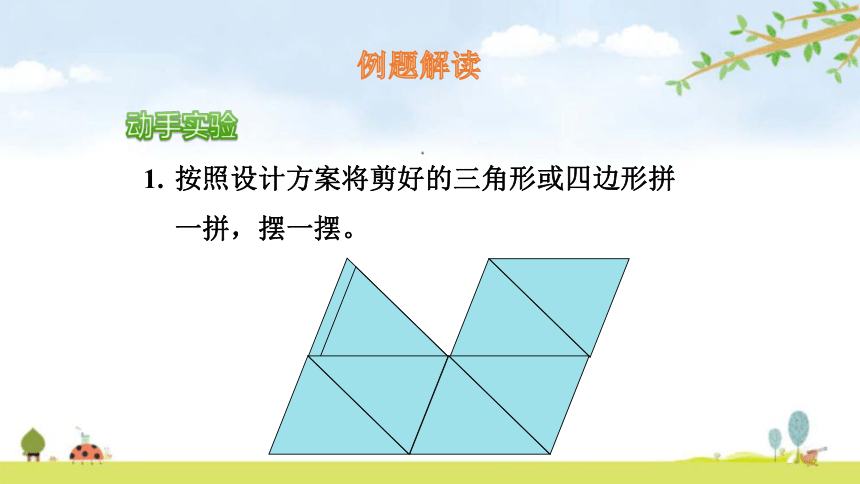
例题解读
动手实验
按照设计方案将剪好的三角形或四边形拼一拼,摆一摆。
例题解读
动手实验
按照设计方案将剪好的三角形或四边形拼一拼,摆一摆。
例题解读
动手实验
按照设计方案将剪好的三角形或四边形拼一拼,摆一摆。
例题解读
动手实验
全班交流密铺的作品,三角形能不能密铺?四边形呢?
观察发现:图形之间都没有空隙,也不重叠,根据密铺的意义可知,三角形和四边形都可以密铺。
例题解读
交流反思
请按照下面的方法试一试,你有什么发现?
将相同图形的角按序号标好,密铺后发现:当摆在一起的图形的角都不同,且两个三角形的三个不同的角分别摆在一起后,正好形成两个共用边的平角,四边形的四个不同的角摆在一起后,正好形成一个周角。
例题解读
2.在上面的活动中,你有什么收获?还有哪些想要进一步研究的问题?
符合密铺要求的多边形应该具备什么样的条件?
只用一种多边形进行密铺,就必须使拼凑在每一个顶点处各角度数之和为360度。
交流反思
例题解读
不是所有的平面图形都可以密铺。看一看,试一试。
由正五边形的内角和=(5-2)×180°=540°,得每个角的度数是540°÷5=108°,108°×3=324°,324°<360°,所以正五边形不能密铺。
由正六边形的内角和=(6-2)×180°=720°,得每个角的度数是720°÷6=120°120°×3=360°,所以正六边形能密铺。
交流反思
例题解读
看一看下面的密铺图案,想一想它们是如何形成的。
第四幅图是由不规则图形密铺成的图案。
第一幅图是由四边形密铺成的图案
第二幅图是由正六边形密铺成的图案
第三幅图是由不规则图形密铺成的图案
交流反思
小结
图形的密铺
三角形和四边形都可以密铺。当围绕一点拼在一起的几个多边形的内角加在一起恰好是360°时,能密铺成一个平面图形。
随堂小测
1.下面的图案可以看成是密铺吗?为什么?
(1)是密铺
(3)不是密铺
有重叠
(2)不是密铺
有空隙
随堂小测
2.下面哪几种图形能密铺,在可以密铺的图形下打“√”。
√
√
√
×
×
随堂小测
3.小小设计师:试试用两种不、同的图形进行密铺。在下面的方格纸上画出你的设计图案。
课后作业
1.从课后习题中选取。
密 铺
数学好玩
学习目标
经历探索平面图形密铺的活动,复习学过的图形知识,初步了解一些平面图形可以密铺的道理。
能进行简单的密铺设计,积累相关活动经验,培养初步的空间观念,提高解决问题的能力。
结合密铺活动感受数学在生活中的广泛应用,发展学生对数学学习的兴趣,结合自我评价发展学生反思能力。
新课引入
新课引入
例题解读
活动任务
三角形能不能密铺?四边形可不可以?
例题解读
设计方案
解决这个问题需要哪些主要步骤?
你想采取怎样的方式解决问题?(独立完成/小组合)如果是小组合作,怎样进行分工?
把主要步骤、分工写下来。
图形的
选择
图形的
准备
小组的
分工
呈现的
方式
……
例题解读
动手实验
按照设计方案将剪好的三角形或四边形拼一拼,摆一摆。
例题解读
动手实验
按照设计方案将剪好的三角形或四边形拼一拼,摆一摆。
例题解读
动手实验
按照设计方案将剪好的三角形或四边形拼一拼,摆一摆。
例题解读
动手实验
全班交流密铺的作品,三角形能不能密铺?四边形呢?
观察发现:图形之间都没有空隙,也不重叠,根据密铺的意义可知,三角形和四边形都可以密铺。
例题解读
交流反思
请按照下面的方法试一试,你有什么发现?
将相同图形的角按序号标好,密铺后发现:当摆在一起的图形的角都不同,且两个三角形的三个不同的角分别摆在一起后,正好形成两个共用边的平角,四边形的四个不同的角摆在一起后,正好形成一个周角。
例题解读
2.在上面的活动中,你有什么收获?还有哪些想要进一步研究的问题?
符合密铺要求的多边形应该具备什么样的条件?
只用一种多边形进行密铺,就必须使拼凑在每一个顶点处各角度数之和为360度。
交流反思
例题解读
不是所有的平面图形都可以密铺。看一看,试一试。
由正五边形的内角和=(5-2)×180°=540°,得每个角的度数是540°÷5=108°,108°×3=324°,324°<360°,所以正五边形不能密铺。
由正六边形的内角和=(6-2)×180°=720°,得每个角的度数是720°÷6=120°120°×3=360°,所以正六边形能密铺。
交流反思
例题解读
看一看下面的密铺图案,想一想它们是如何形成的。
第四幅图是由不规则图形密铺成的图案。
第一幅图是由四边形密铺成的图案
第二幅图是由正六边形密铺成的图案
第三幅图是由不规则图形密铺成的图案
交流反思
小结
图形的密铺
三角形和四边形都可以密铺。当围绕一点拼在一起的几个多边形的内角加在一起恰好是360°时,能密铺成一个平面图形。
随堂小测
1.下面的图案可以看成是密铺吗?为什么?
(1)是密铺
(3)不是密铺
有重叠
(2)不是密铺
有空隙
随堂小测
2.下面哪几种图形能密铺,在可以密铺的图形下打“√”。
√
√
√
×
×
随堂小测
3.小小设计师:试试用两种不、同的图形进行密铺。在下面的方格纸上画出你的设计图案。
课后作业
1.从课后习题中选取。
