四年级下册数学课件-5.4 三角形的内角和-人教版(共19张PPT)
文档属性
| 名称 | 四年级下册数学课件-5.4 三角形的内角和-人教版(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-03 16:35:17 | ||
图片预览



文档简介
(共19张PPT)
5.4 三角形的内角和
5 三角形
学习目标
1.通过实验、操作、推理归纳出三角形的内角和是180°,并能运用三角形的内角和知识解决实际问题,体会转化思想和推理思想。
2.经历利用三角形内角和推导出多边形的内角和的过程,掌握多边形内角和的计算方法。
3.积极参加探索和交流等数学活动,发展初步的空间观念。
新课引入
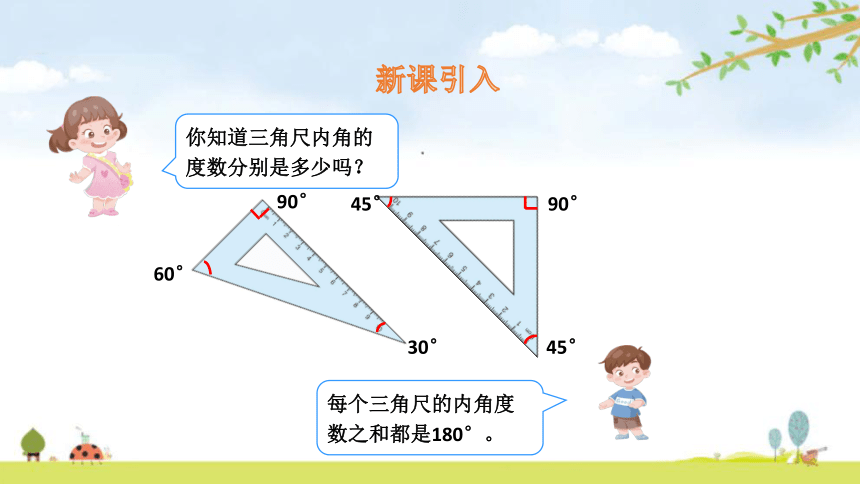
30°
60°
90°
45°
90°
45°
你知道三角尺内角的
度数分别是多少吗?
每个三角尺的内角度
数之和都是180°。
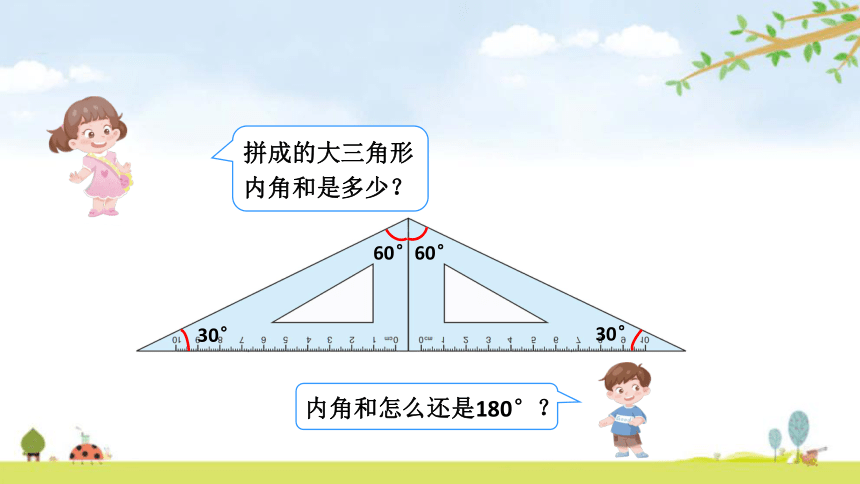
拼成的大三角形内角和是多少?
内角和怎么还是180°?
30°
30°
60°
60°
例题解读
画几个不同类型的三角形。量一量,算一算,三角形3个内角的和各是多少度。
我的这个直角三角形的内角和大约是180°。
我的锐角三角形,也是……
你发现了什么?用实验来验证一下。
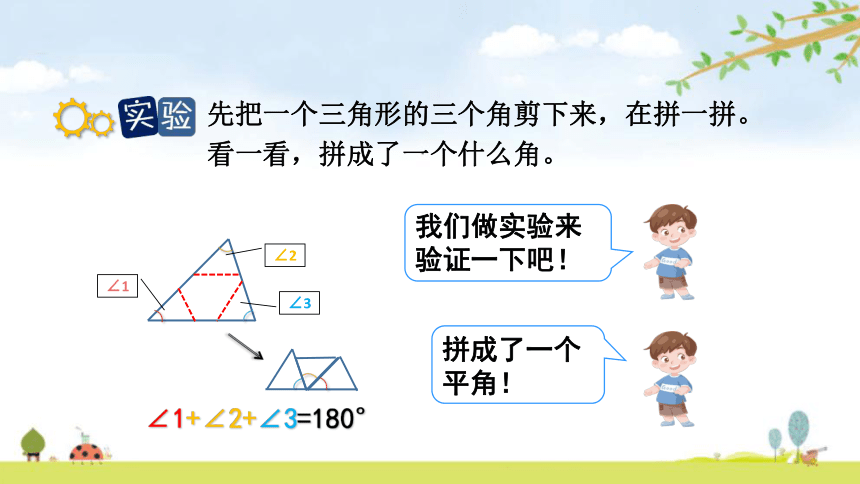
我们做实验来验证一下吧!
先把一个三角形的三个角剪下来,在拼一拼。看一看,拼成了一个什么角。
∠2
∠3
∠1
拼成了一个平角!
∠1+∠2+∠3=180°
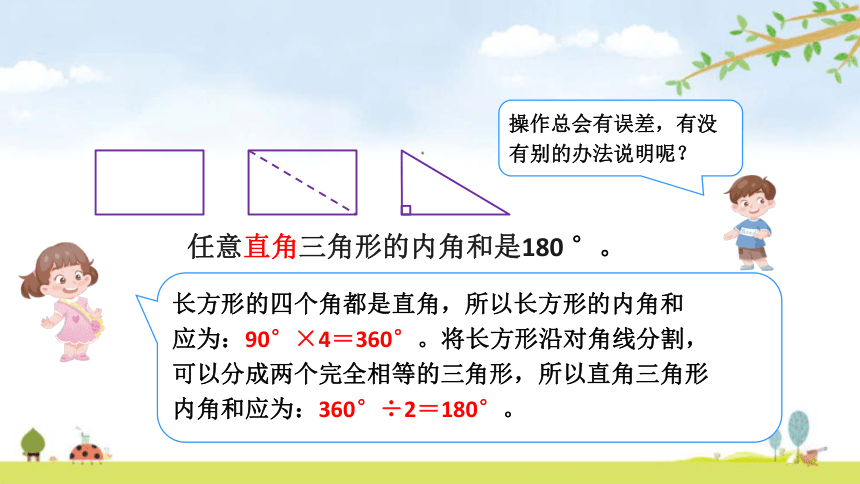
任意直角三角形的内角和是180 °。
长方形的四个角都是直角,所以长方形的内角和
应为:90°×4=360°。将长方形沿对角线分割,
可以分成两个完全相等的三角形,所以直角三角形
内角和应为:360°÷2=180°。
操作总会有误差,有没
有别的办法说明呢?
例题解读
四边形的内角和是多少度?
四边形可以分成几种图形:长方形、正方形、梯形……
阅读与理解
这些图形的内角和是不是一样的呢?
分析与操作
长方形和正方形的4个角都是直角,它们的内角和是360°。
90 ×4=360°
你能想到什么办法求出其他四边形的内角和呢?
可以量出任意一个四边形每个内角的度数,再把它们相加!
方法一
四个角的度数相加刚好为360°
测量法
方法二
我把这个四边形的4个角先剪下来。
我发现它们可以拼成一个周角。
∠1+∠2+∠3+∠4=360°
拼图法
你还能想到哪些方法呢?
方法三
我把这个四边形分成了2个三角形。
一个三角形的内角和是180度,两个相加为360度。
四边形的内角和是_____。
360°
转化法
回顾与反思
我们大家共同证明了所有四边形的内角和都是360°。
答:___________________________。
四边形的内角和是360°
你能想办法求出右边这个多边形的内角和吗?
你是怎么想的呢?
提示:将六边形分成三角形再计算!
小结
多边形的内角和
四边形的内角和是360°
多边形的内角和=180 ×(边数-2)
随堂小测
1. 在右图中,∠1=140°,∠3=25°。求∠2的度数。
∠2 =180 °-140°-25°=15 °
或∠2 =180 °-(140° +25°) =15 °
随堂小测
2. 把下面这个三角形沿虚线剪成两个小三角形,每个小三角形的内角和是多少度?
180°
随堂小测
3. 画一画,算一算,你发现了什么?
6
7
2
3
180 ×5
180 ×4
我发现每个多边形都可以分成
(“边数”-2个)三角形,多边形
的内角和=180°×(边数-2)。
课后作业
1.从课后习题中选取。
5.4 三角形的内角和
5 三角形
学习目标
1.通过实验、操作、推理归纳出三角形的内角和是180°,并能运用三角形的内角和知识解决实际问题,体会转化思想和推理思想。
2.经历利用三角形内角和推导出多边形的内角和的过程,掌握多边形内角和的计算方法。
3.积极参加探索和交流等数学活动,发展初步的空间观念。
新课引入
30°
60°
90°
45°
90°
45°
你知道三角尺内角的
度数分别是多少吗?
每个三角尺的内角度
数之和都是180°。
拼成的大三角形内角和是多少?
内角和怎么还是180°?
30°
30°
60°
60°
例题解读
画几个不同类型的三角形。量一量,算一算,三角形3个内角的和各是多少度。
我的这个直角三角形的内角和大约是180°。
我的锐角三角形,也是……
你发现了什么?用实验来验证一下。
我们做实验来验证一下吧!
先把一个三角形的三个角剪下来,在拼一拼。看一看,拼成了一个什么角。
∠2
∠3
∠1
拼成了一个平角!
∠1+∠2+∠3=180°
任意直角三角形的内角和是180 °。
长方形的四个角都是直角,所以长方形的内角和
应为:90°×4=360°。将长方形沿对角线分割,
可以分成两个完全相等的三角形,所以直角三角形
内角和应为:360°÷2=180°。
操作总会有误差,有没
有别的办法说明呢?
例题解读
四边形的内角和是多少度?
四边形可以分成几种图形:长方形、正方形、梯形……
阅读与理解
这些图形的内角和是不是一样的呢?
分析与操作
长方形和正方形的4个角都是直角,它们的内角和是360°。
90 ×4=360°
你能想到什么办法求出其他四边形的内角和呢?
可以量出任意一个四边形每个内角的度数,再把它们相加!
方法一
四个角的度数相加刚好为360°
测量法
方法二
我把这个四边形的4个角先剪下来。
我发现它们可以拼成一个周角。
∠1+∠2+∠3+∠4=360°
拼图法
你还能想到哪些方法呢?
方法三
我把这个四边形分成了2个三角形。
一个三角形的内角和是180度,两个相加为360度。
四边形的内角和是_____。
360°
转化法
回顾与反思
我们大家共同证明了所有四边形的内角和都是360°。
答:___________________________。
四边形的内角和是360°
你能想办法求出右边这个多边形的内角和吗?
你是怎么想的呢?
提示:将六边形分成三角形再计算!
小结
多边形的内角和
四边形的内角和是360°
多边形的内角和=180 ×(边数-2)
随堂小测
1. 在右图中,∠1=140°,∠3=25°。求∠2的度数。
∠2 =180 °-140°-25°=15 °
或∠2 =180 °-(140° +25°) =15 °
随堂小测
2. 把下面这个三角形沿虚线剪成两个小三角形,每个小三角形的内角和是多少度?
180°
随堂小测
3. 画一画,算一算,你发现了什么?
6
7
2
3
180 ×5
180 ×4
我发现每个多边形都可以分成
(“边数”-2个)三角形,多边形
的内角和=180°×(边数-2)。
课后作业
1.从课后习题中选取。
