2020春北师大版七下数学5.3简单的轴对称图形教学课件(共17张)
文档属性
| 名称 | 2020春北师大版七下数学5.3简单的轴对称图形教学课件(共17张) |

|
|
| 格式 | zip | ||
| 文件大小 | 299.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-03 00:00:00 | ||
图片预览




文档简介
课件17张PPT。5.3简单的轴对称图形1、什么样的图形叫做轴对称图形?
答:把一个图形沿着某条直线对折,如果对折的两部分是完全重合的,我们就称这样的图形为轴对称图形,这条直线叫做这个图形的对称轴.复习提问:?复习提问:?2、下列图形哪些是轴对称图形?引入问题:做一做:试着在纸上画出线段AB及它的中点 O ,再过O点画出与AB垂直的直线CD,沿直线CD将纸对折.看看线段OA与OB是否重合?
线段是不是轴对称图形?ABOCD.如图,直线CD是线段AB的
对称轴,定义:垂直并且平分一条线段的直线称为这条
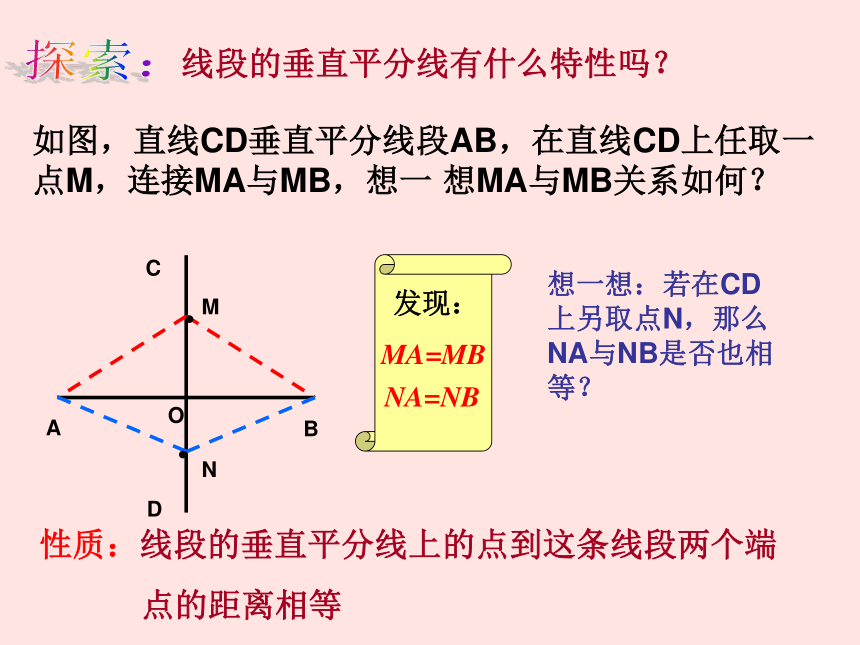
线段的垂直平分线,也叫中垂线.线段是轴对称图形思考:线段的对称轴是什么呢?结论:线段的对称轴是它的垂直平分线它垂直并且平分AB如图,直线CD垂直平分线段AB,在直线CD上任取一点M,连接MA与MB,想一 想MA与MB关系如何?ABC DOMN性质:线段的垂直平分线上的点到这条线段两个端
点的距离相等探索: 发现:
MA=MB
线段的垂直平分线有什么特性吗?想一想:若在CD上另取点N,那么NA与NB是否也相等?NA=NB性质:线段的垂直平分线上的点到这条线段两个端
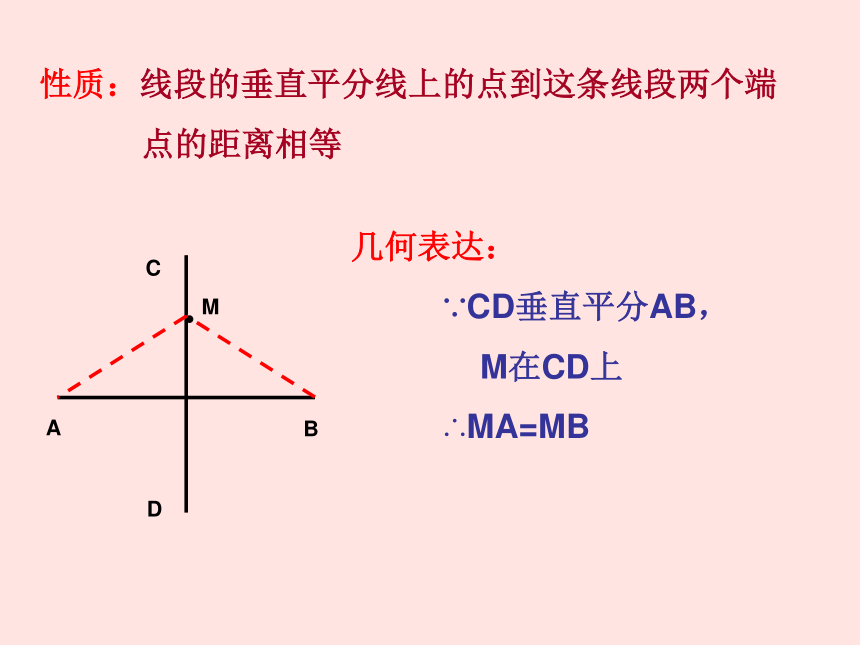
点的距离相等ABC DM几何表达:
∵CD垂直平分AB,
M在CD上
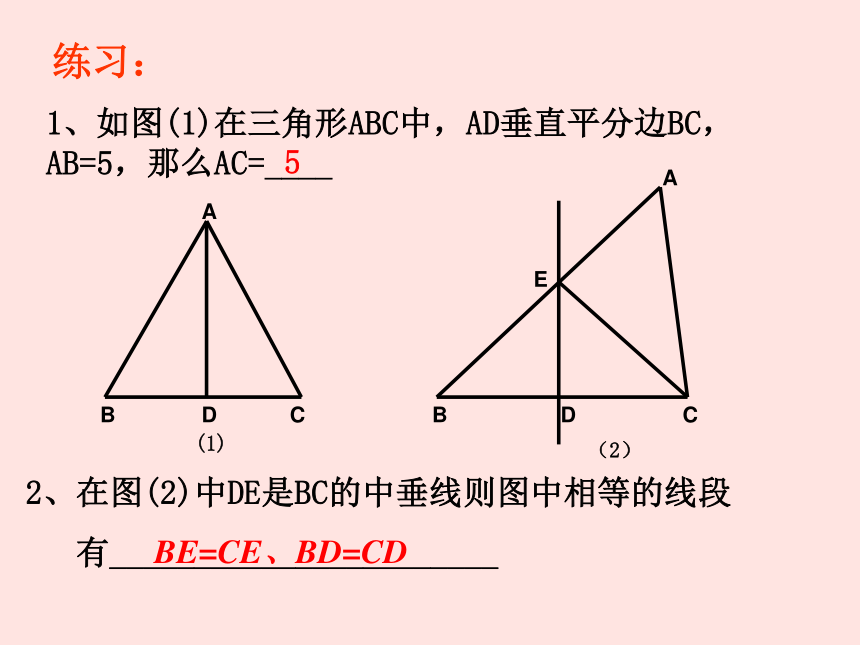
∴MA=MB1、如图(1)在三角形ABC中,AD垂直平分边BC,AB=5,那么AC=____ABCD2、在图(2)中DE是BC的中垂线则图中相等的线段
有_______________________(1)ABCDE(2)5练习:BE=CE、BD=CD例1:△ABC中,BC=10,边BC的垂直平分线分别交AB、 BC于点E、D.BE=6,求△BCE的周长.ABCDE巧解周长:动动手(一)在纸上作出一个角和它的平分线 .猜测:角是轴对称图形吗?如果是,它的对称轴是哪条直线?(二)作一个角的平分线 ,并在平分线上任取一点,作出该点到两边的距离;
猜想:这两个距离相等吗?运动该点,观察这两个距离还相等吗?如果相等,你能说出理由吗?请用自己的语言叙述该结论.角平分线的性质:
角平分线上的点到角两边的
距离相等.练一练:一、填空题:
1.到线段的两个端点距离相等的点有 个.
2.平分一条已知线段的直线有 条;垂直平分一条已知线段的直线有 条.
3.一条已知线段的对称轴有 条.
二、判断题:
4.线段的垂直平分线上存在到这条线段两端点距离不相等的点( )
5.有一公共端点的两条相等线段的图形是轴对称图形 ( )
6.角是轴对称图形,对称轴是角平分线 ( )1、如图,△ABC中BC垂直平分线交AB、BC于点E、D且EB=6△EBC的周长为22则BC长为_____ABCDE2、在上图中△ABC中BC的中垂线交AB于点E
交BC于点D,△AEC的周长是18cm则AB+AC=___练习:10183、在图(2)中MN是DE与BC的中垂线,BD与CE相等吗?为什么?MNBCDE练习:解:∵MN是DE的垂直平分线(已知)∴MD=ME(线段垂直平分线的性质)又∵MN是BC的垂直平分线(已知)∴MB=MC (线段垂直平分线的性质) ∴MB-MD=MC-ME(等式的性质)即:BD=CE作业1.如图,直线l1、l2、l3表示三条相互交叉的公路,现要建一个货物中转站,
要求它到三条公路的距离相等,
则可供选择的地点有( ).
A.1处 B.2处 C.3处 D.4处
2.如图,已知AB=AC,DE垂直
平分线交AB于点D,交AC于点E,若△ABC
的周长为28,BC=8,求△BCE的周长.
3.利用画板探索:△ABC三个角的平分线的位置有什么关系?
1234在△ABC中用刻度尺和量角器画出线段AB、BC、CA的垂直平分线,看看三条垂直平分线的位置有什么关系ABC∟∟∟P试一试:解答:
三条垂直平分线交于一点
思考:若设交点为P,连接PA、PB、PC,那么PA、PB、PC有什么关系?
结论:三角形三条边垂直平分线的交点到三个顶点的距离相等.思考:在△ABC中DE是AC的垂直平分线AE=3cm,△ABD的周长为13cm,求△ABC的周长?ABCDE小结:1、线段是轴对称图形,它的对称轴是它的垂直平分线.2、线段的垂直平分线的定义.3、线段的垂直平分线的性质.4、三角形三条边垂直平分线的交点到三个顶点的距离相等.作业:习题5.3和5.4
答:把一个图形沿着某条直线对折,如果对折的两部分是完全重合的,我们就称这样的图形为轴对称图形,这条直线叫做这个图形的对称轴.复习提问:?复习提问:?2、下列图形哪些是轴对称图形?引入问题:做一做:试着在纸上画出线段AB及它的中点 O ,再过O点画出与AB垂直的直线CD,沿直线CD将纸对折.看看线段OA与OB是否重合?
线段是不是轴对称图形?ABOCD.如图,直线CD是线段AB的
对称轴,定义:垂直并且平分一条线段的直线称为这条
线段的垂直平分线,也叫中垂线.线段是轴对称图形思考:线段的对称轴是什么呢?结论:线段的对称轴是它的垂直平分线它垂直并且平分AB如图,直线CD垂直平分线段AB,在直线CD上任取一点M,连接MA与MB,想一 想MA与MB关系如何?ABC DOMN性质:线段的垂直平分线上的点到这条线段两个端
点的距离相等探索: 发现:
MA=MB
线段的垂直平分线有什么特性吗?想一想:若在CD上另取点N,那么NA与NB是否也相等?NA=NB性质:线段的垂直平分线上的点到这条线段两个端
点的距离相等ABC DM几何表达:
∵CD垂直平分AB,
M在CD上
∴MA=MB1、如图(1)在三角形ABC中,AD垂直平分边BC,AB=5,那么AC=____ABCD2、在图(2)中DE是BC的中垂线则图中相等的线段
有_______________________(1)ABCDE(2)5练习:BE=CE、BD=CD例1:△ABC中,BC=10,边BC的垂直平分线分别交AB、 BC于点E、D.BE=6,求△BCE的周长.ABCDE巧解周长:动动手(一)在纸上作出一个角和它的平分线 .猜测:角是轴对称图形吗?如果是,它的对称轴是哪条直线?(二)作一个角的平分线 ,并在平分线上任取一点,作出该点到两边的距离;
猜想:这两个距离相等吗?运动该点,观察这两个距离还相等吗?如果相等,你能说出理由吗?请用自己的语言叙述该结论.角平分线的性质:
角平分线上的点到角两边的
距离相等.练一练:一、填空题:
1.到线段的两个端点距离相等的点有 个.
2.平分一条已知线段的直线有 条;垂直平分一条已知线段的直线有 条.
3.一条已知线段的对称轴有 条.
二、判断题:
4.线段的垂直平分线上存在到这条线段两端点距离不相等的点( )
5.有一公共端点的两条相等线段的图形是轴对称图形 ( )
6.角是轴对称图形,对称轴是角平分线 ( )1、如图,△ABC中BC垂直平分线交AB、BC于点E、D且EB=6△EBC的周长为22则BC长为_____ABCDE2、在上图中△ABC中BC的中垂线交AB于点E
交BC于点D,△AEC的周长是18cm则AB+AC=___练习:10183、在图(2)中MN是DE与BC的中垂线,BD与CE相等吗?为什么?MNBCDE练习:解:∵MN是DE的垂直平分线(已知)∴MD=ME(线段垂直平分线的性质)又∵MN是BC的垂直平分线(已知)∴MB=MC (线段垂直平分线的性质) ∴MB-MD=MC-ME(等式的性质)即:BD=CE作业1.如图,直线l1、l2、l3表示三条相互交叉的公路,现要建一个货物中转站,
要求它到三条公路的距离相等,
则可供选择的地点有( ).
A.1处 B.2处 C.3处 D.4处
2.如图,已知AB=AC,DE垂直
平分线交AB于点D,交AC于点E,若△ABC
的周长为28,BC=8,求△BCE的周长.
3.利用画板探索:△ABC三个角的平分线的位置有什么关系?
1234在△ABC中用刻度尺和量角器画出线段AB、BC、CA的垂直平分线,看看三条垂直平分线的位置有什么关系ABC∟∟∟P试一试:解答:
三条垂直平分线交于一点
思考:若设交点为P,连接PA、PB、PC,那么PA、PB、PC有什么关系?
结论:三角形三条边垂直平分线的交点到三个顶点的距离相等.思考:在△ABC中DE是AC的垂直平分线AE=3cm,△ABD的周长为13cm,求△ABC的周长?ABCDE小结:1、线段是轴对称图形,它的对称轴是它的垂直平分线.2、线段的垂直平分线的定义.3、线段的垂直平分线的性质.4、三角形三条边垂直平分线的交点到三个顶点的距离相等.作业:习题5.3和5.4
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
