人教版八年级数学下册课件:17.1勾股定理 课件(共18张PPT)
文档属性
| 名称 | 人教版八年级数学下册课件:17.1勾股定理 课件(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 318.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-03 00:00:00 | ||
图片预览


文档简介
(共18张PPT)
人教版八年级数学下
第十七章 勾股定理
17.1.1勾股定理
图2
a
b
c
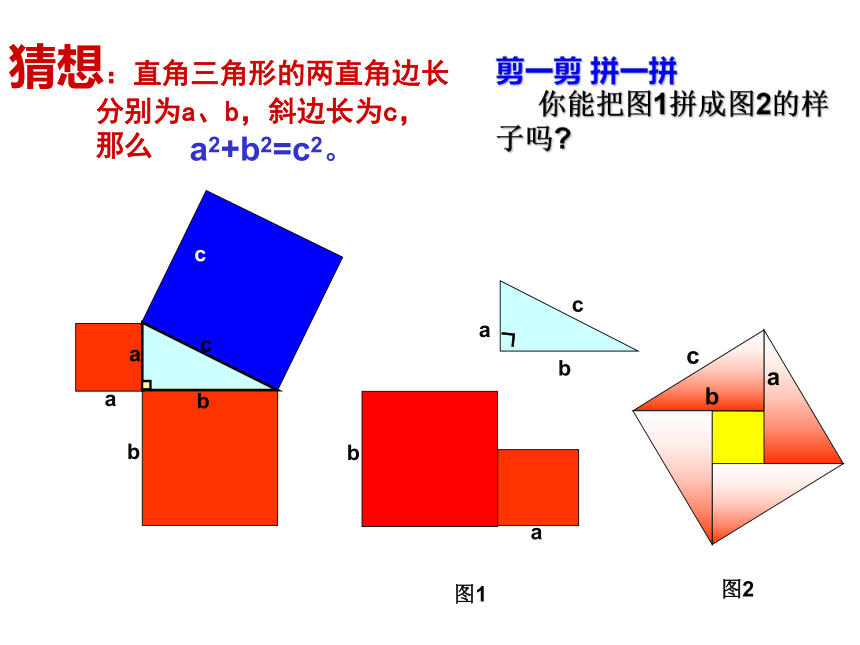
猜想:直角三角形的两直角边长
分别为a、b,斜边长为c,
那么
b
a
c
a2+b2=c2。
a
c
b
┐
图1
b
a
a
b
c
剪一剪 拼一拼
你能把图1拼成图2的样子吗?
(4)
(3)
(2)
(1)
(1)
(2)
(3)
(4)
c
c
c
c
(a-b)2
(a-b)2
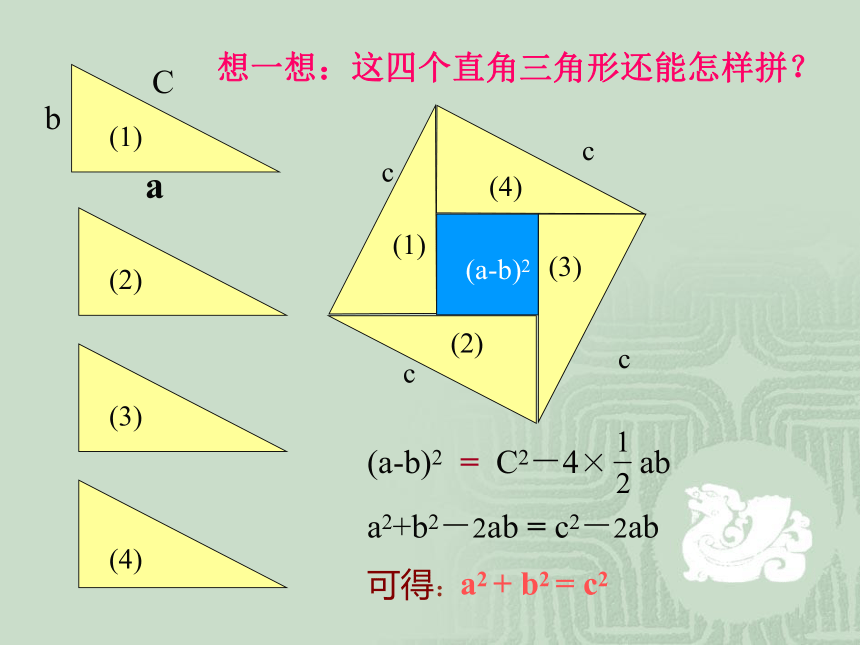
C2-4×
ab
=
a2 + b2 = c2
可得:
a2+b2-2ab = c2-2ab
b
C
a
想一想:这四个直角三角形还能怎样拼?
b
a
b
a
b
a
b
a
c
c
c
c
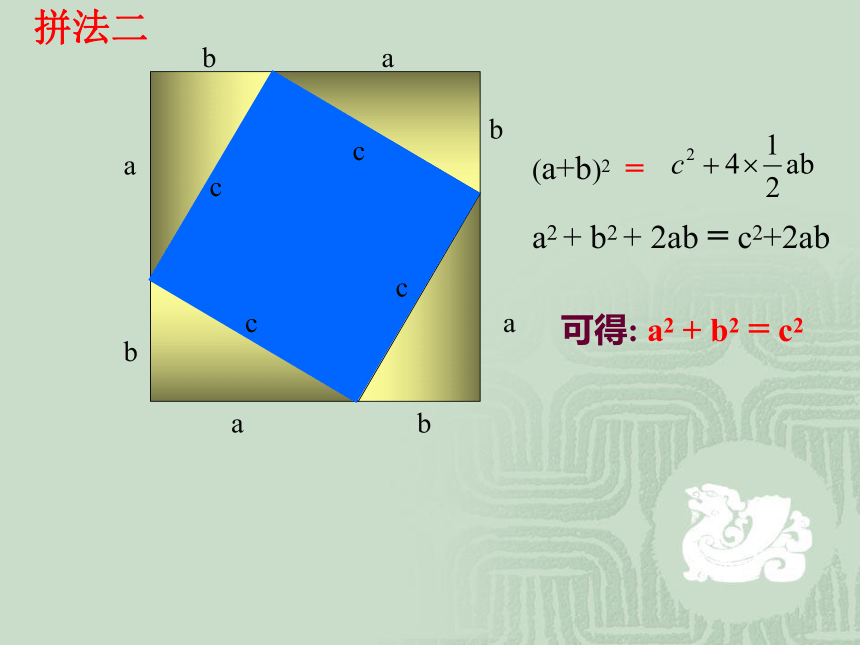
(a+b)2
=
a2 + b2 + 2ab = c2+2ab
可得: a2 + b2 = c2
拼法二
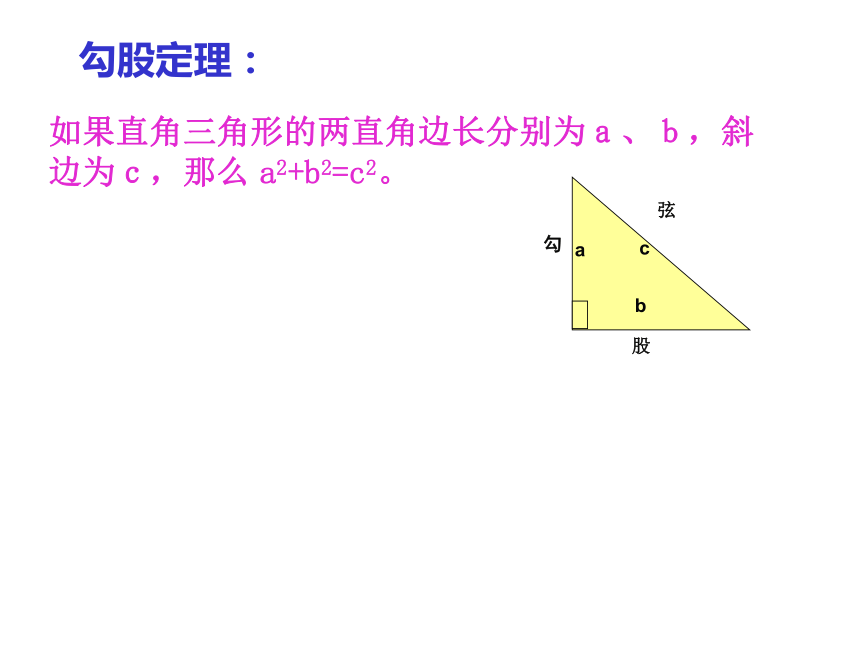
如果直角三角形的两直角边长分别为a、b,斜边为c,那么 a2+b2=c2。
勾股定理:
勾
股
弦
a
b
c
勾股定理的验证方法
证法一、 赵爽弦图验证法
证法二、赵爽弦图的扩充证法
证法三、青朱出入图证法
证法四 、无字证明法
证法五、美国第20任总统伽菲尔德证法
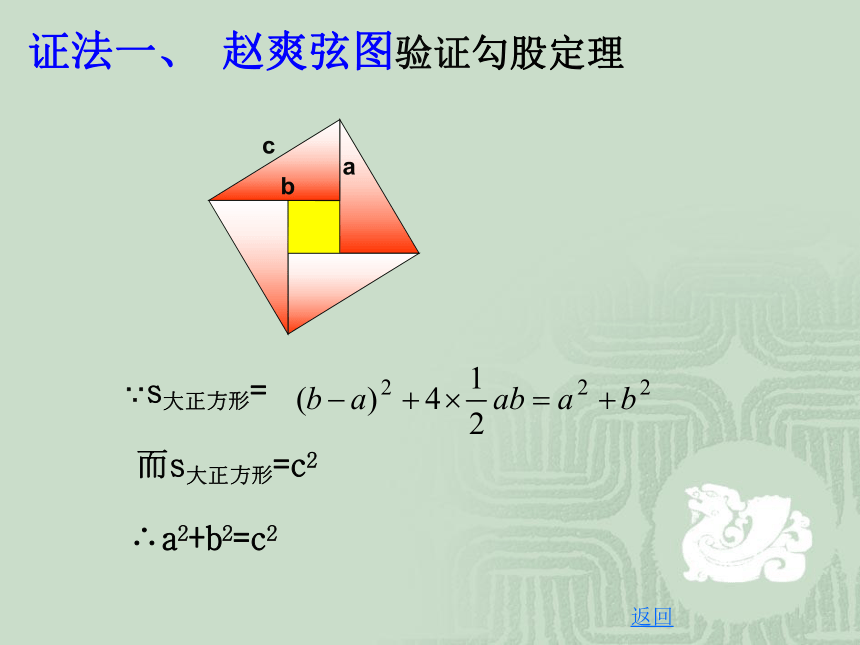
证法一、 赵爽弦图验证勾股定理
∵s大正方形=
a
b
c
而s大正方形=c2
∴a2+b2=c2
返回
b
a
b
a
b
a
b
a
c
c
c
c
(a+b)2
=
a2 + b2 + 2ab = c2+2ab
可得: a2 + b2 = c2
证法二、赵爽弦图的扩充证法
返回
青出
朱入
朱出
朱方
青方
青入
青入
青出
青出
华罗庚
证法三、青朱出入图
朱入
朱出
返回
a
b
c
①
②
③
④
⑤
证法四 无字证明
返回
a
a
b
b
c
c
证法五、美国第20任总统伽菲尔德证法:
∵ s梯形= (a+b)(a+b)= (a2+2ab+b2)
s梯形=2× ab+ c2=ab+ c2
∴ a2+ab+ b2=ab+ c2
∴a2+b2=c2
= a2+ab+ b2
练习:
学以致用:1.求图中字母所代表的正方形的面积。
24
80
A
B
81
144
A
B
400
625
∟
做一做:1
P
625
400
2
6
x
P的面积 =______________
X=____________
225
B
A
C
AB=__________
AC=__________
BC=__________
25
15
20
比一比看看谁算得快!
2.求下列直角三角形中未知边的长:
可用勾股定理建立方程.
方法小结:
8
x
17
16
20
x
12
5
x
做一做
想一想:
小明妈妈买了一部29英寸(74厘米)的电视机,小明量了电视机的屏幕后,发现屏幕只有58厘米长和46厘米宽,他觉得一定是售货员搞错了。你同意他的想法吗?你能解释这是为什么吗?
58厘米
46厘米
74厘米
1、本节课我们经历了怎样的过程?
经历了从实际问题引入数学问题然后发现定理,再到探
索定理,最后学会验证定理及应用定理解决实际问题的过程。
2、本节课我们学到了什么?
通过本节课的学习我们不但知道了著名的勾股定理,还
知道从特殊到一般的探索方法及借助于图形的面积来探索、
验证数学结论的数形结合思想。
3、学了本节课后我们有什么感想?
很多的数学结论存在于平常的生活中,需要我们用数学
的眼光去观察、思考、发现,这节课我们还受到了数学文化
辉煌历史的教育。
作业:
1、通过查阅资料,了解勾股定理的文化背景。
2、通过查阅资料,了解勾股定理的证明方法。
再见
人教版八年级数学下
第十七章 勾股定理
17.1.1勾股定理
图2
a
b
c
猜想:直角三角形的两直角边长
分别为a、b,斜边长为c,
那么
b
a
c
a2+b2=c2。
a
c
b
┐
图1
b
a
a
b
c
剪一剪 拼一拼
你能把图1拼成图2的样子吗?
(4)
(3)
(2)
(1)
(1)
(2)
(3)
(4)
c
c
c
c
(a-b)2
(a-b)2
C2-4×
ab
=
a2 + b2 = c2
可得:
a2+b2-2ab = c2-2ab
b
C
a
想一想:这四个直角三角形还能怎样拼?
b
a
b
a
b
a
b
a
c
c
c
c
(a+b)2
=
a2 + b2 + 2ab = c2+2ab
可得: a2 + b2 = c2
拼法二
如果直角三角形的两直角边长分别为a、b,斜边为c,那么 a2+b2=c2。
勾股定理:
勾
股
弦
a
b
c
勾股定理的验证方法
证法一、 赵爽弦图验证法
证法二、赵爽弦图的扩充证法
证法三、青朱出入图证法
证法四 、无字证明法
证法五、美国第20任总统伽菲尔德证法
证法一、 赵爽弦图验证勾股定理
∵s大正方形=
a
b
c
而s大正方形=c2
∴a2+b2=c2
返回
b
a
b
a
b
a
b
a
c
c
c
c
(a+b)2
=
a2 + b2 + 2ab = c2+2ab
可得: a2 + b2 = c2
证法二、赵爽弦图的扩充证法
返回
青出
朱入
朱出
朱方
青方
青入
青入
青出
青出
华罗庚
证法三、青朱出入图
朱入
朱出
返回
a
b
c
①
②
③
④
⑤
证法四 无字证明
返回
a
a
b
b
c
c
证法五、美国第20任总统伽菲尔德证法:
∵ s梯形= (a+b)(a+b)= (a2+2ab+b2)
s梯形=2× ab+ c2=ab+ c2
∴ a2+ab+ b2=ab+ c2
∴a2+b2=c2
= a2+ab+ b2
练习:
学以致用:1.求图中字母所代表的正方形的面积。
24
80
A
B
81
144
A
B
400
625
∟
做一做:1
P
625
400
2
6
x
P的面积 =______________
X=____________
225
B
A
C
AB=__________
AC=__________
BC=__________
25
15
20
比一比看看谁算得快!
2.求下列直角三角形中未知边的长:
可用勾股定理建立方程.
方法小结:
8
x
17
16
20
x
12
5
x
做一做
想一想:
小明妈妈买了一部29英寸(74厘米)的电视机,小明量了电视机的屏幕后,发现屏幕只有58厘米长和46厘米宽,他觉得一定是售货员搞错了。你同意他的想法吗?你能解释这是为什么吗?
58厘米
46厘米
74厘米
1、本节课我们经历了怎样的过程?
经历了从实际问题引入数学问题然后发现定理,再到探
索定理,最后学会验证定理及应用定理解决实际问题的过程。
2、本节课我们学到了什么?
通过本节课的学习我们不但知道了著名的勾股定理,还
知道从特殊到一般的探索方法及借助于图形的面积来探索、
验证数学结论的数形结合思想。
3、学了本节课后我们有什么感想?
很多的数学结论存在于平常的生活中,需要我们用数学
的眼光去观察、思考、发现,这节课我们还受到了数学文化
辉煌历史的教育。
作业:
1、通过查阅资料,了解勾股定理的文化背景。
2、通过查阅资料,了解勾股定理的证明方法。
再见
